Сигналы (коды) Баркера.

В 50—60-е годы ХХ в. были найдены целые классы секвентных сигналов с совершенными корреляционным свойствами. Среди них большую известность получили сигналы (коды, последовательности) Баркера. Эти сигналы обладают уникальным свойством – независимо от номера позиции М = n в этих последовательностях значения их автокорреляционных функций при всех n ≠ 0 не превышают единицы (т.е. абсолютное значение «остатков» – боковых лепестков – не превышает 1/n основного). В то же время энергия всех этих сигналов численно равна n.

Сигналы Баркера в настоящее время удается реализовать лишь при числе позиций М = 2, 3, 4, 5, 7, 11 и 13. Случаи М = 2 и М = 3 являются тривиальными. В качестве иллюстрации на рис. 13.3 приведен вид 13-позиционного сигнала Баркера, его фазовое кодирование и АКФ.

Функции Уолша

Дальнейшим развитием систем функций типа последовательностей Радемахера, стала ортонормированная система функций (последовательностей) Уолша (Walsh). Широко используемые в технике связи последовательности Уолша – одни из немногих известных в математике с 1922 г. ортонормированных функций, которые на отрезке своего существования (периоде следования – Т/2, Т/2) принимают лишь два значения: +1 или – 1.

Введем безразмерное время, нормированное к периоду следования

θ= t/Т; и обозначим k-ю (k – порядок) функцию Уолша принятым в математике символом wal(k, θ). Идею построения последовательностей можно уяснить из рис. 13.4, где показаны первые восемь функций. Ортонормированность данных функций следует из принципа их построения, и может быть проверена непосредственно путем вычисления интеграла. Система wal(k, θ) позволяет продемонстрировать наиболее важные свойства функций Уолша, которые определяются следующим разностным (рекурентным) уравнением:

wal(2k + р, θ) = (–1)^{[k/2] +p} [wal(k,2θ + 0,5) + (–1)^{k +p} wal(k,2θ – 0,5)]

где обозначение [k/2] представляет собой наибольшее целое число, меньшее или равное k/2; параметр р может принимать только два значения: 1 или 0.

Функции Уолша нормированы к единице при любом порядке k:

|| wal(k, θ)||² = 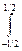wal²(k, θ)dθ = 1.

Из рис.13.4 можно заметить, что четным относительно середины интервала определения (θ = 0) функциям wal(k, θ) соответствуют четные номера k, а нечетным функциям – нечетные номера

Поэтому в ряде случаев используются обозначения cal(k, θ) для четных функций и sal(k, θ) для нечетных функций Уолша. Эти функции связаны следующими соотношениями:

cal(k, θ) = wal(2k, θ); sal(k, θ) = wal(2k–1, θ).

Способ нумерации функций Уолша в системе называется

упорядочением. Разработаны и существует несколько принципов

упорядочения функций Уолша. Функции Уолша, показанные на рис. 13.4,

упорядочены по Уолшу. В ряде практических задач удобнее пользоваться другими способами упорядочения. Наиболее часто применяются системы функций Уолша, упорядоченные по Адамару (Hadamard) [had(h, θ)] и по Пэли (Peley) [pal(p, θ)].

ПРИМЕР 13.3.

На некотором интервале разложения Т₀ определить спектр отрезка синусоиды единичной амплитуды u(t) = sin 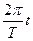(рис. 13.5) в базисе функций Уолша.

Р е ш е н и е. Интервал разложения Т₀ в этом случае целесообразно приравнять периоду синусоиды Т. Как это принято в функциях Уолша, перейдем к безразмерному времени θ= t/Т и запишем исходное колебание u(t) в форме u(θ) = sin2πθ. Для сокращения выкладок ограничимся 16-ю функциями, причем сначала выберем упорядочение по Уолшу.

Поскольку заданная функция u(θ) нечетна относительно точки

θ = 1/2, то все коэффициенты при четных функциях, т. е. при cal(k, θ), равны нулю. Остальные восемь функций wal(k, θ); имеют периодичность внутри интервала [0, 1] кратную периоду функции u₁(θ), также приводят к нулевым коэффициентам. Таким образом, не равны нулю U(1), U(5), U(9), U(13). Они будут равны:

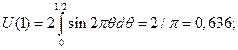
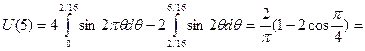–0,265;

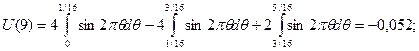
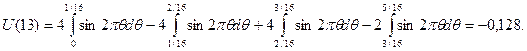
Спектр исследуемого сигнала u₁(θ), в базисе функций Уолша представлен на рис. 13.5, б Восстановление исходного сигнала (рис. 13.5, а) шестнадцатью функциями Уолша показано на рис. 13.5, в (двенадцать спектральных коэффициентов превращаются в нуль). Для более удовлетворительной апроксимации синусоидального колебания в базисе Уолша требуется существенное увеличение числа спектральных компонентов.