Дискретный (ортогональный) вейвлет-анализ

Им называют представление дискретных сигналов в виде обобщенного ряда Фурье по системе ортогональных базисных функций, формирующихся из некоторого исходного (порождающего) вейвлета ψ(t) Применяется ортогональный вейвлет-анализ в основном для сжатия данных (информации) и подавления шумов.

В дискретном вейвлет-анализе применена музыкальная терминология. Набор значений вейвлет-преобразования при фиксированном масштабе а, называют голосом, диапазон масштабов (или, что то же самое, частот) от а до 2а, – октавой. Согласно музыкальной классике, на каждую октаву следует брать, по крайней мере, 12 голосов.

Упрощенно, идею многомасштабного дискретного вейвлет-анализа можно трактовать так: «большое» пространство «всех анализируемых сигналов» надо заполнить растянутыми или сжатыми копиями некоего «эталонного» пространства, порожденного элементарным сигналом ψ(х) и его сдвигами по оси времени. По определению это эталонное пространство принимается за набор сигналов, которые можно представить с разрешением 1.(Рис. 14.3).

Пусть функция φ(х) – исходный единичный заштрихованный «столбик» на интервале [0, 1]; его сдвиги – аналогичные столбики на интервалах ..., [-2, -1], [-1, 0], [1, 2],... (рис.14.3, а). Пространство сигналов (в нашем случае анализируемый сигнал u(t))состоит из «лесенок», полученных умножением этих столбиков на определенные числа. Остальными пространствами сигналов служат перемасштабированные копии этих наборов столбиков. Одно из них получается растяжением вдвое – рис. 14.3, б). Для исходного сигнала φ(х) необходимо, чтобы, его сдвиги вида φ(х – 1), φ(х – 2), ... φ(х – k),... были друг другу ортогональны. В итоге получится

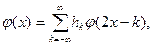(14.4)

где h_k – некоторые коэффициенты.

В рассматриваемом примере для функции φ(х) коэффициенты h_k равны 1 и 1, а для ψ(х) соответственно 1 и –1.

Ортогональные вейвлеты замечательны тем, что существует быстрый алгоритм разложения по ним любого сигнала. Сам вейвлет показан на рис. 14.3, в и г; система его сдвигов и двоичных растяжений и сжатий – это широко известный базис на основании функций А.Хаара (A. Haar), разработанный им еще в 1909 г. (рис. 14.3, д)