Понятие о корреляционном анализе

Корреляционный анализ «пришел» в радиотехнику в конце 40-х годов ХХ века, а фундаментальная теорема Хинчина-Винера свзала его и гармонический анализ в единое целое.

На практике, часто наряду со спектральным исследованием сигналов, оказывается полезным анализ характеристики, дающей представление о скорости изменения во времени, а также длительности сигнала без разложения его на гармонические оставляющие.

Пусть копия сигнала u(t-τ) смещена относительно своего оригинала

u(t) на некоторый интервал времени τ. Для количественной оценки степени отличия (связи) исходного сигнала u(t) и его смещенной во времени копии u(t-τ) используют автокорреляционную (корреляционную) функцию (АКФ).

Для детерминированного сигнала конечной длительности (финитного сигнала) аналитическая запись АКФ представляет собой интеграл вида

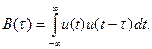(13.1)

Формула (13.1) показывает, что при отсутствии сдвига (τ=0) АКФ имеет положительное значение и достигает максимальной величины, равной энергии сигнала:

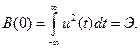(13.2)

Такая энергия [Дж] выделяется на резисторе с сопротивлением 1 Ом, если к его выводам подключить напряжение u(t) [B].

Одним из важнейших свойств АКФ является ее четность: В(τ) = В(-τ),

что легко доказывается.

Для периодического сигнала с периодом Т, энергия которого бесконечно велика, вычисление АКФ невозможно, В этом случае вычисляют АКФ за период

. (13.3)

ПРИМЕР 13.1. Для прямоугольного видеоимпульса, имеющего амплитуду Е и длительность τ_И определить автокорреляционную функцию.

Р е ш е н и е. Для этого примера вычисления удобнее провести графически. На рис. 13.1 показано построение АКФ для прямоугольного импульса. При данных построениях на рис. 13.1, а...в приведены соответственно: исходный импульс u(t) = u, сдвинутая на интервал τ его копия u_τ(t)= u(t–τ)= u_τ и их произведение u(t) u(t–τ)= u u_τ.

Интеграл (13.1), в данном случае наиболее просто и наглядно вычислить путем графических построений. Произведение u(t) u(t–τ) не равно нулю на интервале времени, когда имеется наложение друг на друга любых частей сигнала и его копии и достигает максимума при τ= 0. Найденная АКФ имеет вид равнобедренного треугольника с шириной основания в два раза больше длительности прямоугольного импульса и высотой, определяемой энергией сигнала В(0) = Е² τ = Э (рис. 13.1, г). В радиоэлектронике часто вводят удобный для анализа сигналов числовой параметр – интервал корреляции, графически равный ширине основания АКФ. Для данного примера интервал корреляции τ_к = 2 τ_И.

Пример 13.2. Определить автокорреляционную функцию гармонического сигнала u(t) = U_mcos(ωt + φ) c ненулевой начальной фазой (рис. 13.2, а).

Р е ш е н и е. Используя формулу (13.3) и обозначив В_n(τ) = R(τ), находим

.

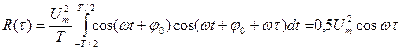Автокорреляционная функция гармонического сигнала любого вида имеет размерность мощности и не зависит от начальной фазы колебания φ₀ (рис.13.2).