Связь между энергетическим спектром и АКФ сигнала

Допустим, что некоторый импульсный сигнал u(t) имеет спектральную плотность S(ω). C помощью (13.1) определим АКФ, записав заданный сигнал u(t) в виде обратного преобразования Фурье (1.17):

.

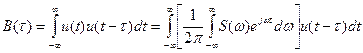Для упрощения вычислений введем новую переменную х = t - τ. Затем,

сделав в последнем выражении ряд перестановок, получим

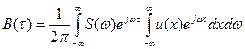. (13.4)

Здесь интеграл 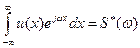(13.5) есть функция, комплексно-сопряженная со спектральной плотностью сигнала S(ω). Поэтому формула (13.4) примет вид:

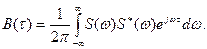(13.6)

Функцию W_И(ω) = S(ω) S*(ω) = | S(ω)|² (13.7)

называют энергетическим спектром (спектральной плотностью энергии) сигнала, который показывает распределение его энергии по оси частот. Физическая размерность энергетического спектра сигнала W_И(ω) – В² с/Гц.

Учитывая соотношение (13.7), окончательно получим выражение для АКФ аналогового детерминированного сигнала

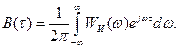(13.8)

Как следует из этой формулы, автокорреляционная функция представляет собой обратное преобразование Фурье от энергетического спектра. Очевидно, что имеется и прямое преобразование Фурье от автокорреляционной функции:

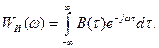\ (13.9)

Прямое преобразование Фурье (13.9) автокорреляционной функции соответствует энергетическому спектру, а обратное преобразование Фурье энергетического спектра (13.8) – автокорреляционной функции детерминированного сигнала.

Данные результаты имеют фундаментальное значение в радиоэлектронике и важны по двум причинам:

1. Исходя из распределения энергии по спектру, становится возможным оценить корреляционные свойства сигналов – чем шире энергетический спектр сигнала, тем меньше интервал корреляции. Соответственно, чем больше интервал корреляции сигнала, тем короче (в частотной области) его энергетический спектр.

2. Соотношения (13.8) и (13.9) позволяют экспериментально определить одну из функций по значению другой.

На практике часто удобнее вначале получить автокорреляционную функцию, а затем с помощью прямого преобразования Фурье вычислить энергетический спектр сигнала. Этот прием широко применяется при анализе свойств сигналов в реальном масштабе времени, т.е. без временн′ой задержки при его обработке.