Дискретные сигналы, их описание и характеристики

Преобразование непрерывного сигнала x(t) в дискретный цифровой сигнал осуществляется в аналого-цифровом преобразователе (АЦП). Процесс формирования дискретного сигнала в АЦП можно представить в виде идеализированной модели (рис. 3.6), представляющей собой ключ К, работой которой управляет генератор, задающий необходимую частоту дискретизации F₀=1/Δ (где Δ – интервал дискретизации).

При времени преобразования АЦП, существенно меньшем интервала дискретизации Δ, можно сказать, что АЦП осуществляет импульсную модуляцию непрерывного сигнала. В момент замыкания ключа на выходе АЦП появится импульс, амплитуда которого соответствует мгновенному значению исходного непрерывного сигнала x(t).

Следовательно, при работе АЦП непрерывный сигнал x(t), рассматриваемый на интервале [0,T], будет характеризоваться своими отсчетными значениями x₀, x₁,…, x_N-1, взятыми в моменты времени 0, Δ,…, (N-1)Δ. Полное число отсчетов N=T/Δ.

Математическую модель конкретного сигнала x_д(t) на интервале [0, T] можно представить в виде последовательности δ – импульсов, сдвинутых на интервал дискретизации [11]

(3.30)

где x_k =x(kΔ) – отсчетное значение аналогового сигнала x(t) в момент времени t=kΔ; δ(t-kΔ) – δ-функция на k интервалов дискретизации.

Рис.3.6. Идеализированная модель преобразования непрерывного сигнала в дискретный

а – исходный непрерывный сигнал; б – структурное представление процесса дискретизации; в – дискретизированный сигнал

Итак, после преобразования в АЦП массив чисел x₀, x₁,…, x_N-1 является единственной информацией, по которой можно судить о спектральных свойствах непрерывного сигнала x(t). Как и для случая непрерывных сигналов, методика изучения дискретных сигналов состоит в том, что полученная выборка отсчетных значений мысленно повторяется бесконечно большое число раз, в результате чего дискретный сигнал становится периодическим. Затем этот сигнал представляется в виде комплексного дискретного ряда Фурье, коэффициенты которого будут характеризовать спектральные свойства дискретного периодического сигнала.

Комплексный ряд Фурье дискретного сигнала x_д(t) имеет вид [11]

(3.31)

коэффициенты C_n которого определяются через отсчетные значения x_k из соотношения

(3.32)

и образуют так называемое дискретное преобразование Фурье (ДПФ) рассматриваемого сигнала x_д(t). Это преобразование принято называть прямое ДПФ, а выражение (3.31) – обратным ДПФ.

Дискретное преобразование Фурье обладает следующими основными свойствами [12]:

1. ДПФ есть линейное преобразование, т. е. сумме сигналов соответствует сумма их ДПФ.

2. Число n различных коэффициентов C_n равно числу отсчетов N за период T, при этом, если n=N, коэффициент C_N= C₀.

3. Коэффициент C₀ (постоянная составляющая) является средним значением всех отсчетов, т. е.

.

4. Если число отсчетов N – четное число, то

.

5. Если значения x_k – вещественные числа, то коэффициенты ДПФ, номера которых располагаются симметрично относительно N/2, образуют комплексно-сопряженные пары, т.е.

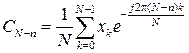
После несложных преобразований выражение можно представить в виде

и тогда получим, что C_N-n=C_n^*. Поэтому считают, что коэффициенты ,…,C_N-1 соответствуют отрицательным частотам и их можно не вычислять.

Аналогично преобразованию Фурье для непрерывного сигнала модуль |C_n| коэффициента ДПФ определяет амплитуду n–ой гармоники дискретного сигнала, а диаграмма изменения модулей всех коэффициентов ДПФ является спектральной плотностью S_хд(ω) дискретного сигнала x_д(t) при выбранном значении интервала дискретизации. При этом спектральная плотность S_хд(ω) является периодической функцией частоты с периодом ω, а изменение интервала дискретизации Δ приводит к изменению числа отсчетов, амплитуды и числа гармоник полученного дискретного сигнала.

Покажем, что полученная модель дискретного сигнала соответствует реальному сигналу и что на основании этой модели можно используя дискретные преобразования Фурье восстановить непрерывный сигнал x(t).

Пусть дана совокупность отсчетов x₀, x₁,…, x_N-1 некоторого дискретного сигнала x_Д(t), найдены также коэффициенты ДПФ C₀, С₁…, C_N/2, то по ним всегда можно восстановить исходный сигнал x(t), который подвергся дискретизации. Для этого записывается ряд Фурье в виде конечной суммы, которая определяет непрерывный сигнал в виде [11]:

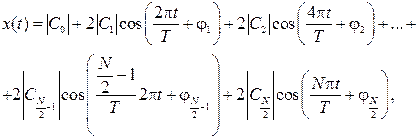(3.33)

где φ – фазовый угол соответствующего коэффициента ДПФ, определяемое выражением

Следует подчеркнуть, что восстановление непрерывного сигнала по полученной формуле есть не приближенная, а точная операция, полностью эквивалентная получению текущих значений сигнала с ограниченным спектром по его отсчетам.

Задачу дискретного спектрального анализа можно поставить и по-иному.

Пусть известны коэффициенты С_n дискретного преобразования Фурье.

Тогда для решения данной задачи воспользуемся выражением для обратного преобразования Фурье дискретного сигнала:

Определим значение сигнала x_д(t) при t=kΔ с учетом того, что в приведенном выражении суммированию подлежит лишь конечное число членов ряда, которые соответствуют гармоникам, содержащимся в спектре исходного сигнала x(t), определенного на интервале [0, T]. Тогда

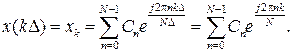(3.34)

Полученная формула определяет алгоритм обратного дискретного преобразования Фурье (ОДПФ).

Взаимно дополняющие друг друга формулы прямого и обратного ДПФ являются дискретными аналогами пары преобразований Фурье для непрерывных сигналов, приведенных в табл. 3.2.

Таблица 3.2.

Дискретное преобразование Фурье	Непрерывное преобразование Фурье

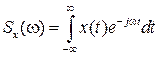
Как видно из формул (3.32) и (3.34), чтобы выполнить прямое или обратное дискретное преобразование Фурье последовательности из N элементов, требуется выполнить N операций с комплексными числами. Если длины обрабатываемых массивов имеют порядок 1000 или более, то использовать эти алгоритмы дискретного спектрального анализа в реальном масштабе времени затруднительно из-за ограниченного быстродействия вычислительных устройств.

Ускорить преобразования дискретного сигнала позволяет алгоритм быстрого преобразования Фурье (БПФ), который был разработан в 60-х годах. Существенное сокращение числа выполняемых операций в алгоритме БПФ удается за счет того, что обработка входного массива сводится к нахождению ДПФ или ОДПФ массивов с меньшим числом членов.

При реализации алгоритма БПФ предполагается, что число отсчетов дискретного сигнала {x_k}N=2^P, P – целое число. Далее выполняются следующие операции [12]:

1. Входная последовательность {x_k} разбивается на две части с четными и нечетными номерами:

{x_k}_чт={x_2k}, {x_k}_нч={x_2k+1}, k=0,1,..., .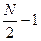

2. Определяется n-й коэффициент ДПФ в виде

(3.35)

где {x_{k чт}} и {x_{k нч}} – это k-й четный и нечетный члены последовательности {x_k}.

3. Первая половина коэффициентов ДПФ исходного сигнала с номерами от 0 до 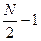выражается через коэффициенты ДПФ двух частных последовательностей:

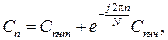
(3.36)

где С_nчт и С_nнч – коэффициенты, соответствующие аналогичным членам последовательности {x_k}.

Следует учесть, что последовательность коэффициентов, относящихся к четной С_nчт или нечетной С_nнч частям входного массива, является периодической с периодом N/2, т.е.

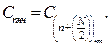
4. Находим выражение для второй половины множества коэффициентов ДПФ в виде:

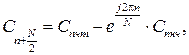n=0,1,..., 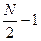, (3.37)

предварительно преобразовав множитель, входящий в зависимость (3.36) при n≥N/2 в соответствии с выражением

5. На основании формул (3.36) и (3.37), лежащих в основе алгоритма БПФ, далее проводят вычисления соответствующих коэффициентов по итерационному принципу: последовательность отсчетов с четными и нечетными номерами вновь разбивается на две части. Процесс продолжают до тех пор, пока не получится последовательность, состоящая из единственного элемента. При этом БПФ этого элемента будет совпадать с ним самим.

При реализации алгоритма БПФ число операций, необходимых для вычисления ДПФ, оценивается как N·log₂ N.

По аналогии со сверткой непрерывных сигналов

(3.38)

при описании дискретных сигналов вводят понятие дискретной свертки, которая представляется совокупностью своих отсчетных значений:

(3.39)

Если для сигналов x_д(t) и y_д(t) определены коэффициенты дискретного преобразования Фурье C_xn и C_yn, то отсчетные значения дискретной свертки сигналов определяются как

(3.40)

т. е. коэффициенты ДПФ C_fn свертки являются произведениями коэффициентов ДПФ свертываемых сигналов

(3.41)

Этот результат имеет большое значение в теории дискретных сигналов и цифровых фильтров. Если выборки сигналов достаточно длинны (несколько тысяч элементов), то для вычисления их свертки целесообразно вначале найти их ДПФ, перемножить коэффициенты, а затем воспользоваться формулой для определения отсчетных значений свертки.

При анализе и синтезе дискретных и цифровых устройств широко используют так называемое Z-преобразование, которое играет по отношению к дискретным сигналам такую роль, как интегральные преобразования Лапласа и Фурье по отношению к непрерывным сигналам.

Пусть известна числовая последовательность {x_k}=(x₀, x₁,…, x_i,…) конечная или бесконечная, содержащая отсчетные значения некоторого дискретного сигнала x_д(t). Поставим этой последовательности в однозначное соответствие сумму ряда по отрицательным степеням комплексной переменной z вида

(3.42)

Если эта сумма существует (ряд сходится), то ее называют Z-преобразованием числовой последовательности или отсчетных значений дискретных сигналов.

Целесообразность введения такого математического преобразования определена тем, что свойства дискретных последовательностей чисел (дискретных сигналов) можно изучать, исследуя их Z-преобразования обычными методами математического анализа.

Полагая, что отсчеты {x_k} есть значения непрерывной функции x(t) в точках t=kΔ, любому непрерывному сигналу также можно поставить в соответствие Z-преобразование при выбранном шаге дискретизации

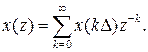(3.43)

Замечательное свойство Z-преобразования состоит в том, что функция x(z) определяет всю бесконечную совокупность отсчетов дискретного сигнала (x₀, x₁,…), которую можно определить, используя формулу для обратного Z-преобразования

(3.44)

где ∮ интеграл по контуру, при вычислении которого используется фундаментальное свойство теоремы Коши

(3.45)

Важное значение имеют следующие свойства Z-преобразования [12]:

1. Z-преобразование – линейная операция, т. е. если для дискретных сигналов {x_k} и {y_k} известны соответствующие Z-преобразования x(z) и y(z), то сигналу {U_k}={ax_k+by_k} будет соответствовать Z-преобразование U(z)=aX(z)+bY(z) при любых постоянных a и b.

2. Z-преобразование смещенного дискретного сигнала {y_k}, получающегося из дискретного сигнала {x_k} путем сдвига на один шаг дискретизации в сторону запаздывания, определяется как

т.е. символ z^-1 служит оператором единичной задержки на один интервал дискретизации в z-области.

3. Z-преобразование свертки {F_k} двух дискретных сигналов {x_k} и {y_k} соответствует произведение Z-преобразований свертываемых сигналов, т.е.

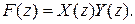
4. Z-преобразование однозначно связано с преобразованием Лапласа и Фурье. Если дискретный сигнал можно представить в виде идеальной импульсной последовательности

то преобразование его по Лапласу имеет следующее изображение:

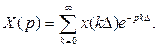
Полученное выражение непосредственно переходит в Z-преобразование, если выполнить подстановку 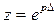, т.е.

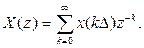
Если положить то выражение

будет являться преобразованием Фурье импульсной последовательности.

Связь Z-преобразования с преобразованиями Лапласа и Фурье позволяет проводить формальную аналогию между временными и спектральными свойствами непрерывных и дискретных сигналов.

Важной задачей при проектировании измерительных каналов ИВС является рациональный выбор интервала дискретизации, поскольку при малом интервале дискретизации может оказаться неоправданно большое число точек отсчета, и наоборот, при большом интервале дискретизации могут иметь место большие потери информации.

При решении данной задачи необходимо преобразовать непрерывный сигнал в последовательность дискретных значений, взятых через определенный интервал дискретизации, при котором погрешность восстановления исходного непрерывного сигнала по дискретным отсчетам не будет превышать заданного значения.

Для решения этой задачи необходимо получить соотношение, связывающее величину интервала дискретизации Δ с погрешностью δ_диск восстановления исходного сигнала при последующей обработке. Эти соотношения наиболее просто получаются на основе рассмотрения спектральных характеристик непрерывного и дискретного сигналов.

Пусть x(t) – непрерывный детерминированный сигнал, который имеет частотный спектр (или спектральную плотность S(ω)), ограниченный верхней частотой ω_max=2πF_max. Тогда спектр частот (или спектральная плотность дискретизированного сигнала) представляет собой результат суммирования бесконечного числа "копий" спектра исходного сигнала.

Эти копии располагаются на оси частот (рис. 3.8) через равные промежутки соответствующие частоте дискретизации F₀, т. е.

или (3.46)

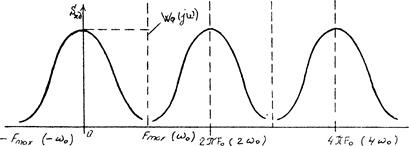
Рис.3.8. Спектральная диаграмма дискретного сигнала

Если F_max – верхняя граничная частота в спектре исходного сигнала, то при

боковые лепестки спектральной диаграммы перестанут накладываться друг на друга и спектральная плотность дискретизированного ряда будет описываться выражениями (3.29). Такой непрерывный сигнал, подвергнутый импульсной дискретизации, может быть вновь восстановлен с помощью идеального фильтра нижних частот W_ф(jω), если на вход фильтра подать импульсную последовательность вида (3.46). Наибольшее значение интервала дискретизации составит , что соответствует известной теореме Котельникова.

(!!!Теорема Котельникова упоминается лишь вскользь здесь и на стр. 172, при этом ничего не говорится о том, каким образом необходимо восстанавливать без потерь сигнал дискретизированный в соответствии с этой теоремой).

Рассмотренные модели и характеристики непрерывных и дискретных измерительных сигналов являются основой для описания процессов их выделения, преобразования и обработки в каналах измерительных приборов и систем.