Принципы помехоустойчивого кодирования

Теоретической основой построения эффективных кодов является теорема кодирования 1 К. Шеннона, доказывающая (приведена в упрощенном виде), что для канала связи без помех всегда можно создать систему экономного кодирования дискретных сообщений, у которой среднее количество двоичных кодовых сигналов на один символ сообщения будет приближаться как угодно близко к энтропии источника сообщений.

Базой для помехоустойчивого кодирования является теорема кодирования 2 К.Шеннона, в которой утверждается, что для канала связи с помехами всегда можно создать систему кодирования, при которой сообщения будут переданы со сколь угодно высокой степенью верности, если только производительность источника не превышает пропускной способности канала связи.

Различают помехоустойчивые коды с обнаружением и исправлением ошибок.

Код с обнаружением ошибок уменьшает число неверно опознанных сообщений или позволяет особо отмечать сообщения, в которых установлено присутствие ошибки, а в некоторых случаях (системы с обратными информационными связями) принять меры к повторной передаче и приему неопознанных сообщений. Простейшим является код с проверкой на четность. На передающем конце канала связи устройство кодирования проводит подсчет числа логических «1» в передаваемом двоичном кодовом слове. Если сумма «1» оказывается нечетной, в конце передаваемой кодовой комбинации добавляется «1», а если нет, то «0». На приемном конце канала связи проводится аналогичный подсчет, и если контрольная сумма (число единиц в принятой кодовой комбинации) будет нечетной, то принимается решение о том, что при передаче произошло искажение информации, в противном случае принятая информация признается достоверной.

Код с исправлением ошибок позволяет получать верные сообщения, несмотря на наличие некоторого числа ошибок при опознании символов.

При этом, чтобы исправить одну ошибку, разрешенные комбинации должны отличаться друг от друга как минимум на три символа . В этом случае одиночная ошибка переведет переданное слово в одно из запрещенных, что и позволить обнаружить ошибку. От остальных разрешенных слов оно будет отличаться не менее чем на два символа, что и позволит исправить ошибку.

По способу внесения избыточности в передаваемые последовательности, коды разделяются на блочные и непрерывные.

При блочном (сосредоточенном) кодировании каждому дискретному сообщению соответствует кодовое слово с определенными числом и значением символов.

При непрерывном (рассредоточенном) кодировании в безызбыточную последовательность информационных символов (последовательность слов простого кода) включаются избыточные символы, размещение которых сообразуется лишь с видом вносимых ошибок и может не зависеть от положения границ первоначальных слов простого кода.

Характеристикой корректирующего кода является его избыточность

R = 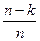, (12.11)

или скорость передачи 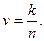(12.12)

где n – общее число символов в кодовом слове с избыточностью; k – число символов в слове при передаче тех же сообщений простым кодом.

ПРИМЕР 12.2. Для блочного кода с длиной слова n = 15, исправляющего две ошибки, k = 7 и R = (15 – 7)/15 = 0,533, а при n = 15 и исправлении трех ошибок k = 5 и R = (15 – 5)/15 = 0,666. Соответственно v = 0,467 и 0,333.

Как видно, при данной длине блоков n повышение корректирующей способности связано с увеличением избыточности R и уменьшением скорости передачи v.

Коды, у которых требуемая корректирующая способность достигается при минимальной избыточности, называются оптимальными.