Понятие о цифровых фильтрах

Цифровым фильтром называют цифровое вычислительное устройство, преобразующее последовательность числовых отчетов {u(k∆t)} = { u_Т} = {u_k} в последовательность числовых отчетов {y(k∆t)} = { y_ц}. = { y_k}.выходного сигнала {u_k} → { y_k}, в предположении, что некоторая последовательность чисел {u_k} представляет собой массив отсчетов входного сигнала u(t), взятых обязательно с интервалом дискретизации Котельникова (Найквиста) ∆t.

Выходным сигналом цифрового фильтра пусть будет последовательность цифровых отсчетов { y_k}. Для описания реакции цифрового фильтра на входное воздействие в виде дискретной последовательности чисел используют его импульсную характеристику {h(k∆t)} = {h_k} = h_k. Из теории цифровых фильтров известно, что упомянутая импульсная характеристика представляет собой дискретную последовательность чисел, являющуюся его реакцией на «единичный импульс» – дискретизированную дельта-функцию δ(k∆t) = δ_k – (в цифровом представлении это 1, 0, 0, 0, ...):

(1, 0, 0, 0, ...) → {h₀, h₁, h₂, ... h_k } = h_k.

Импульсную характеристику h_k цифрового фильтра можно трактовать как результат дискретизации согласно теоремы отсчетов непрерывной импульсной характеристики h(t) cоответствующего аналогового линейного фильтра. В цифровых фильтрах импульсные характеристики могут иметь конечное и бесконечное число отсчетов (рис. 10.3)

Рассмотрим принцип действия цифрового фильтра с простейшими алгоритмом фильтрации и импульсной характеристикой с ограниченным числом отсчетов (рис. 10.4). Пусть входная последовательность {u_k} из четырех единичных дискретных отсчетов u₀, u₁, u₂, u₃ непрерывного сигнала u(t) подается на вход цифрового фильтра с импульсной характеристикой {h_m} в виде трех отсчетов h₀ = 1,5; h₁= 1, h₂= 0,5 (рис. 10.4, а, б). В результате некоторых заданных операций на выходе фильтра возникает последовательность отсчетов {y_k}.

При воздействии первого отсчета сигнала u₀ = 1 на выходе фильтра формируется последовательность откликов, определяемых его импульсной характеристикой. Таких отсчетов будет три и они имеют значения: 1,5; 1; 0,5 (Рис. 10.4, в). Эта последовательность опишется формулой: u₀ h_m.

Воздействие второго отсчета u₁ = 1 приведет к появлению на выходе фильтра последовательности еще трех откликов 1.5; 1; 0,5 (Рис. 10.4, г ), которые аналитически можно выразить так u₁ h_m-1.

То же произойдет при отклике цифрового фильтра на действие остальных отсчетов входной последовательности (Рис. 10.4, д – е). В результате прохождения всего входного сигнала из k на выходе цифрового фильтра с импульсной характеристикой h_m создастся сумма откликов 1,5; 2,5; 3; 3; 1,5; 0,5 (Рис. 10.4, ж) Общее выражение для выходных отсчетов примет вид

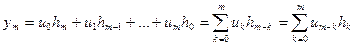(10.1)

Cоотношение (10.1) определяет алгоритм линейной цифровой фильтрации во временн'ой области и показывает, что выходная последовательность представляет собой дискретную свертку входного сигнала с имппульсной характеристикой цифрового фильтра. Полное число выходных отчетов при этом составляет N = m + k -1.

Системная функция является отношением z-преобразования выходного сигнала к z-преобразованию входного сигнала и связана с импульсной характеристикой формулой:

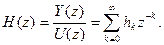(10.2)

Цифровые фильтры делятся на два больших класса: нерекурсивные и рекурсивные (рекурсия – циклическое обращением к вычисленным данным).