Преобразование Фурье.

Часто математическое описание даже несложных по структуре детерминированных сигналов является весьма трудной задачей. Поэтому в радиоэлектронике и технике связи используется оригинальный прием, при котором реальные, сложные по структуре и форме сигналы заменяют (представляют, аппроксимируют) набором (взвешенной суммой) идеализированных математических моделей, описываемых элементарными функциями. Это дает важный инструмент для анализа прохождения сигналов через радиотехнические цепи. Подобным образом можно упростить обратную задачу – синтез сложных сигналов из совокупности простых.

Идея принадлежит физику и математику Фурье, он показал, что любое изменение во времени некоторой функции можно представить (аппроксимировать) в виде конечной или бесконечной суммы ряда гармонических колебаний с разными амплитудами, частотами и начальными фазами. Этой функцией может быть, в частности, ток или напряжение в некоторой электрической цепи.

Пусть на заданном интервале времени t₁, t₂ действует произвольный непрерывный сигнал u(t) и для его аппроксимации используется система идеализированных функций v_i(t), являющаяся ортонормированной (независимой и приведенной к единице). Тогда данный сигнал может быть представлен обобщенным рядом Фурье

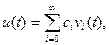(1.6)

где с_i – некоторые постоянные коэффициенты, для базисных функций (v_k)

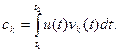(1.7)

Совокупность коэффициентов c_k полностью определяет анализируемый сигнал u(t) и называется его спектром.

Достаточно распространенное использование в теории сигналов обобщенного ряда Фурье связано с его очень важным свойством: при выбранной ортонормированной системе функций v_k(t) и фиксированном числе слагаемых ряда (1.6) он обеспечивает наилучшую аппроксимацию заданного сигнала u(t).

В радиотехнике и теории связи наибольшее применение получили ортонормированные базисы тригонометрических (синусоидальных и косинусоидальных) функций. Это обусловлено следующим: гармонические колебания наиболее просто генерировать; гармоническое колебание теоретически полностью сохраняет форму при прохождении через любую линейную цепь с постоянными параметрами, а изменяется при этом лишь его амплитуда и начальная фаза. Операцию представления непрерывных детерминированных сигналов в виде совокупности постоянной составляющей и суммы гармонических колебаний с кратными частотами принято называть спектральным разложением (представлением) или гармоническим анализом.

Периодическим называют любой сигнал (функцию), повторяющийся через регулярные интервалы времени и удовлетворяющий условию

u(t) = u(t + nT), где Т – период повторения или следования импульсов; п = 0, 1, 2 … .

При спектральном представлении периодических сигналов наиболее удобен ортонормированный базис гармонических функций:

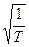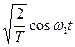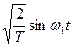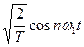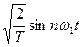, , , … , , , (1.8)

где ω₁ = 2π/T ― частота следования сигнала.

Наиболее распространенная тригонометрическая форма ряда Фурье периодического сигнала

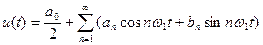. (1.9)

В этом соотношении имеются следующие компоненты сигнала:

− постоянная составляющая:

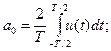(1.10)

−амплитуды косинусных составляющих:

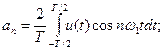(1.11)

− амплитуды синусоидальных составляющих:

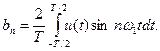(1.12)

Иногда применяют эквивалентную форму ряда Фурье

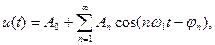
где 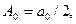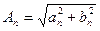− амплитуда, а 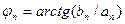− начальная фаза n-й гармоники сигнала.

В радиоэлектронике и теории сигналов также широко используется комплексный ряд Фурье

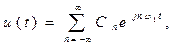(1.13)

где 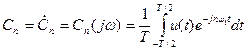(1.14)

− комплексная амплитуда n-й гармоники.

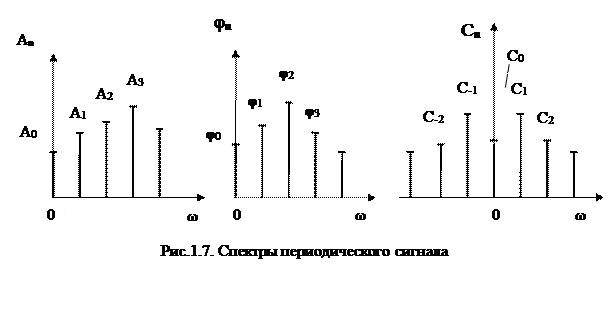
Наиболее наглядно о спектре радиотехнического сигнала можно судить по его графическому изображению – спектральной диаграмме. Совокупность амплитуд гармонических составляющих А_n носит название спектра амплитуд, φ_n – спектра фаз, С_n – комплексного спектра (рис. 1.7).