Амплитудная модуляция

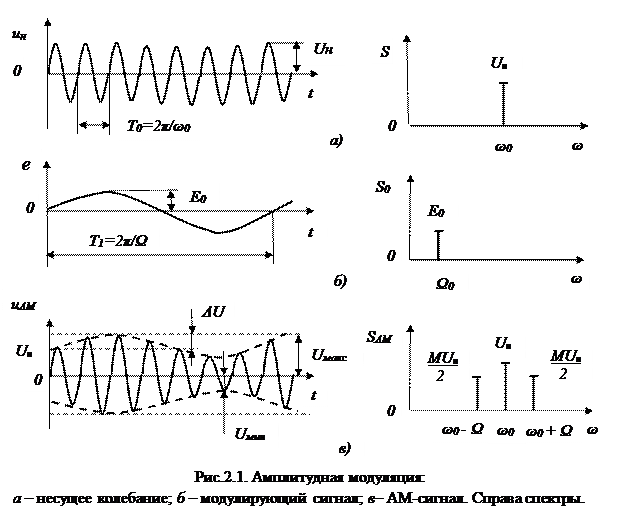
В процессе осуществления амплитудной модуляции несущего колебания вида (рис. 2.1)

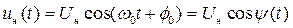, (2.1)

его амплитуда должна изменяться по закону:

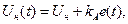(2.2)

где U_н – амплитуда в отсутствие модуляции; ω₀ – угловая (круговая) частота; φ₀ – начальная фаза; ψ(t) = ω₀t + φ₀ – полная (текущая или мгновенная) фаза; k_A – безразмерный коэффициент пропорциональности; e(t) – модулирующий сигнал.

Функцию U_н(t) в радиотехнике называют огибающей амплитудно-модулированного сигнала (АМ-сигнала).

Подставив (2.2) в (2.1) получим

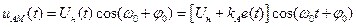(2.3)

Для однотонального сигнала ,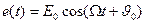

где E₀ – амплитуда; Ω = 2π/Т₁ – круговая частота; Т₁ – период; θ₀ – начальная фаза;

окончательно будет

u_АМ(t) = U_н(1+МсоsΩt)cosω₀t, (2.4)

где М = k_AE₀ = ΔU/U_н – коэффициент или глубина модуляции.

Для определения спектра АМ-сигнала, используя в выражении (2.4) тригонометрическую формулу произведения косинусов, получим

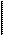
(2.5)

Из формулы (2.5) видно, что при однотональной модуляции спектр АМ-сигнала состоит из трех высокочастотных составляющих. Первая из них

представляет собой исходное несущее колебание с амплитудой U_н и частотой ω₀ . Колебания с частотами ω₀ + Ω и ω₀ − Ω называются соответственно верхней и нижней боковыми составляющими. Амплитуды боковых составляющих одинаковы, и равны МU_н/2 и расположены

симметрично относительно несущей частоты сигнала ω₀. Ширина спектра АМ-сигнала при однотональной модуляции Δ ω_АМ = 2 Ω = 4πF, где F – циклическая частота модуляции (см. рис.2.1).