Спектры непериодических колебаний

В теории спектрального представления непериодических сигналов (импульсных) сигналов используют искусственный прием, формально заменяя такие сигналы периодическими с бесконечно большим интервалом (периодом) следования Т → ∞.

При увеличении периода следования импульсов Т линейный спектр будет все более плотным. В предельном случае, когда период Т → ∞, равные расстояния между спектральными линиями уменьшаются настолько, что спектр становится сплошным, а амплитуды отдельных спектральных составляющих окажутся бесконечно малыми. При этом частота следования импульсов ω₁ = 2π/T → 0 и превращается в dω, дискретная переменная nω₁ — в мгновенную (текущую частоту ω, а сумма трансформируется в интеграл. Периодическая последовательность импульсов u_n(t) станет одиночным импульсом u(t) и выражение (1.14) запишется в виде

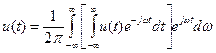(1.15)

Здесь интеграл в скобках является комплексной функцией частоты. Обозначив его

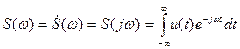(1.16)

получим 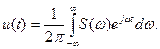(1.17)

Соотношения (1.16) и (1.17) носят фундаментальный характер в теории сигналов и называются соответственно прямым и обратным преобразованиями Фурье. Они связывают между собой вещественную функцию времени (сигнал) u(t) и комплексную функцию частоты S(ω), которую называют спектральной плотностью. Она характеризует интенсивность сплошного распределения амплитуд гармоник непериодического сигнала вдоль оси частот ω.

Дискретный спектр периодического и спектральная плотность непериодического сигналов имеют разные размерности. Дискретный спектр имеет размерность амплитуды (В или А), спектральная плотность имеет размерность В/Гц или А/Гц.

Вследствие того, что непериодический сигнал u(t) и его спектральная плотность S(ω) взаимно однозначно связаны парой преобразований Фурье, последние позволяют аналитически отыскать спектральную плотность по заданной форме сигнала, и наоборот, его форму по спектральной плотности.

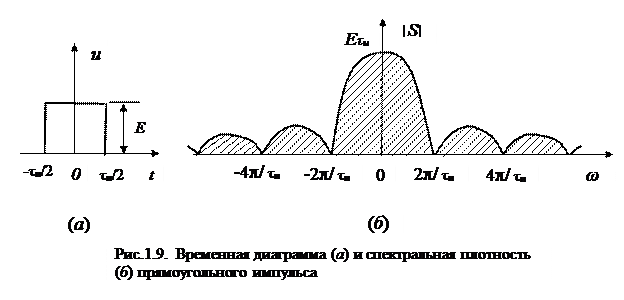
Временная диаграмма и спектральная плотность прямоугольного импульса приведены на рис. 1.9.

Случайные сигналы.

Большинство реальных радиотехнических сигналов в той или иной степени носят случайный характер, т.е. ряд их параметров меняется во времени случайным образом. Поэтому случайные сигналы (или случайные процессы) описываются статистическими (вероятностными) законами. Примером случайного процесса может служить напряжение на входе приемника v(t) = u(t) + х(t). Регистрируя напряжение v(t) в данный момент, нельзя с полной определенностью предсказать, каково будет его значение в последующие моменты времени, т.к. u(t) изменяется случайным образом в соответствии с передаваемым сообщением, к тому же сигнал подвергается воздействию различных аддитивных помех х(t), имеющих случайный характер.

Одной из важных характеристик случайной величины Х(t₁) является интегральная функция распределения F(х). Для любой случайной величины Х(t₁) принимающей любые вещественные значения, интегральная функция распределения определяется на интервале 0 ≤ F(х) ≤ 1.

Если случайная величина Х(t₁) является непрерывной во времени, то удобно пользоваться ее производной

,

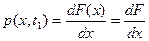получившей название одномерной плотности распределения вероятности.

Математическое ожидание

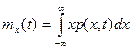
представляет собой среднее значение случайного процесса в текущий момент времени t.

Дисперсия

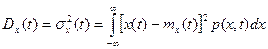
характеризует разброс мгновенных значений относительно его среднего значения.

Нормальный (Гауссовский) случайный процесс характерен для шумов и помех, имеющих место в аналоговых каналах систем радиосвязи, и поэтому удобен при анализе случайных сигналов с нормальным распределением плотности вероятности и представляет собой функцию вида

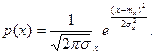
Для анализа радиотехнических цепей и сигналов большой практический интерес представляет специфический случайный процесс, теоретически имеющий равномерный спектр мощности во всей полосе частот, получивший название «белый шум», по аналогии с применяемым в оптике понятием «белый свет», который содержит все цвета спектра.

W_x(ω) = W₀, -∞ < ω < ∞.