Рассмотрим теперь дифференциальную форму теоремы Остроградского-Гаусса.
Пусть в некоторой точке 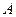 с координатами
с координатами 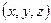 существует напряженность
существует напряженность
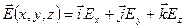
Построим около точки 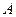 прямоугольный бесконечно малый параллелепипед объемом
прямоугольный бесконечно малый параллелепипед объемом 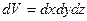 .
.
Пусть объемная плотность заряда в нем равна 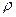 и зависит от координат выбранной точки поля:
и зависит от координат выбранной точки поля: 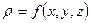 .
.
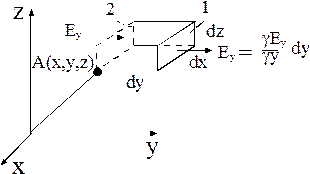 Поток вектора
Поток вектора 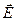
· через правую грань (1)
равен:
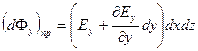 ,
,
· а через левую (2):
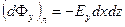 ,
,
· Поэтому поток вдоль оси 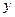 равен
равен
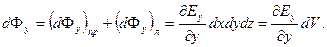
Таким же образом для верхней и нижней грани получим: 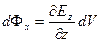 ,
,
для задней и передней: 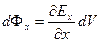 .
.
По теореме Гаусса 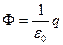 ,
,
причем 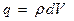 - заряд, заключенный внутри объема
- заряд, заключенный внутри объема 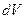 (ввиду малости
(ввиду малости 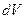 можно считать что
можно считать что 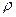 внутри параллелепипеда всюду одинакова),
внутри параллелепипеда всюду одинакова),
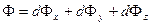 ,
,
Тогда 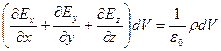 ,
,
Или 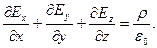
Сумма, стоящая в левой части, называется дивергенцией вектора 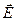 ,
,
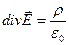 , или
, или 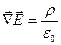
-дивергенция вектора напряженности равна объемной плотности зарядов, создающих поле, деленной на 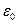 .
.
Это выражение представляет собой теорему Гаусса в дифференциальной форме.
Она характеризует поле в точке.
Электрические заряды являются источниками и стоками поля вектора 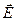 .
.
Линии вектора 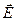 начинаются и заканчиваются на электрических зарядах.
начинаются и заканчиваются на электрических зарядах.
· Если 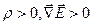 - это источник поля
- это источник поля 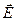 ,
,
· если 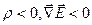 - сток поля.
- сток поля.
· Если 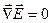 , то в данной точке нет зарядов, линии
, то в данной точке нет зарядов, линии 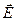 не прерываются.
не прерываются.
Дата добавления: 2020-12-11; просмотров: 486;











