Устойчивость стержня на упругом основании

Гораздо чаще, чем изолированные стержни, в конструкциях ЛА используются стержни, скрепленные или иногда выполненные «зацело» с пластинами и оболочками. Это стрингеры и всевозможные ребра, окантовывающие панели, люки и т.п. Расчетная модель таких элементов - стержень, лежащий на упругом основании, препятствующем его прогибу.

Наиболее распространенная модель упругого основания предложена Винклером. Реакция (отпор) “винклеровского” основания 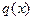в любой точке определяется величиной прогиба стержня только в этой точке и не зависит от формы прогиба. В соответствии с этим

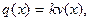(8.1)

где 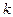- коэффициент упругости основания (коэффициент постели), в общем случае переменный.

Линеаризованное уравнение устойчивости такого стержня может быть получено добавлением к (5.8) поперечной нагрузки (8.1)

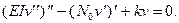(8.2)

Граничные условия формулируются как для изолированного стержня (см. Лек-цию 5). Ограничимся анализом уравнения (8.2) для случая, когда его коэффициенты постоянны, т.е.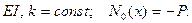

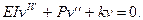(8.3)

Записав общее решение этого уравнения в виде

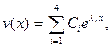(8.4)

где

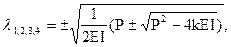(8.5)

мы для любых однородных граничных условий найдем спектр собственных значений, наименьшее из которых будет 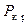, и спектр собственных функций.

Можно поступить и иначе.

Из теории задач на собственные значения известно, что система собственных функций 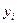любой задачи на собственные значения для обыкновенного дифференциального уравнения вида

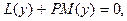
где 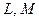- некоторые дифференциальные операторы, обладает полнотой и ортогональностью:

.

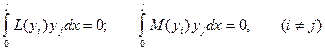Это дает основание предположить, что собственные функции краевых задач для стержня без упругого основания могут оказаться собственными и для стержня на упругом основании.

Действительно, для свободного стержня

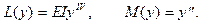
Следовательно,

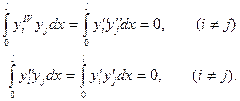(8.6)

Кроме того собственные функции уравнения

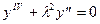
при шарнирно опертом правом конце, т.е. при

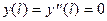(8.7)

оказываются собственными (см. Лекцию 5) и для уравнения

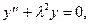
а это означает, что кроме (8.6) ортогональны и сами функции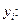

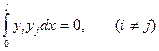(8.8)

Таким образом, при граничных условиях (8.7) собственные функции уравнения (8.3) пр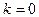и и 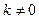совпадают.

Пусть концы балки шарнирно оперты. Для этого случая собственные функции свободного стержня

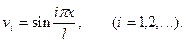(8.9)

Подставив любую из них в (8.3), имеем

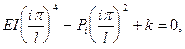(i=1,2,…) (8.10)

откуда

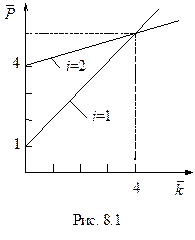
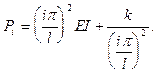(8.11)

С учетом выражения для 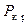свободного стержня

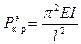
перепишем (8.11) в виде

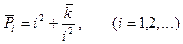(8.12)

где

.

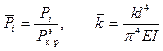Из собственных значений 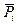надо выбрать наименьшее. В отличие от свободного стержня оно может реализовываться не при 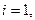что соответствует одной полуволне синусоиды, а при различных 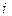в зависимости от 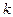(рис.8.1). Чем жестче основание, тем по большему числу полуволн будет терять устойчивость шарнирно опертый стержень.

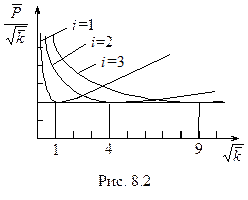
Возможна и иная графическая интерпретация зависимости (8.12) (рис.8.2).

Легко видеть, что при увеличении жесткости основания форма потери устойчивости может измениться скачкообразно.

Кроме того, критическая сила с увеличением длины стержня не уменьшается монотонно, а может даже возрастать.

При достаточно большой длине 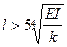критическая сила практически перестает зависеть от длины стержня и можно принять

Упругое основание, на котором лежит стержень, может быть не только непрерывным, но и дискретным (рис. 8.3). Так, например, стрингер может быть оперт по концам или в пролете на упругие шпангоуты или поперечный набор стрингеров. Кроме дискретных опор может присутствовать и непрерывное основание.

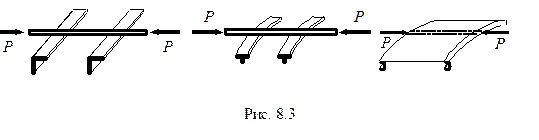
Рассмотрим возможные подходы к решению таких задач.

А. Пусть непрерывное основание отсутствует, а концы стержня оперты упруго или даже упруго защемлены.

В этом случае стержень можно рассматривать как изолированный, а упругость опор учесть граничными условиями (см. Лекцию 5).

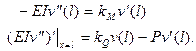(8.13)

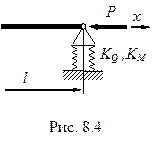
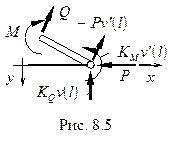
Коэффициенты упругост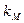и и 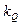определяют экспериментально, либо из решения задачи для опоры под действием соответствующего сосредоточенного фактора.

Б. Пусть стержень оперт на несколько упругих опор.

К решению такой задачи также можно подойти по-разному. Например, на основе метода начальных параметров (см. Лекцию 6).

Записав решения для каждого из пролетов в форме (6.10), (6.11), мы должны затем “склеить” их над каждой из упругих опор. Условия склейки в отличие от (6.8) будут содержать реакции упругих опор:

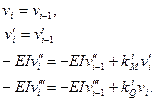(8.14)

Возможен и другой подход к решению этой задачи. Дискретный отпор упругого основания описывается как непрерывный с помощью обобщенных функций:

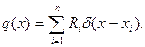
Здесь 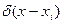- дельта-функция Дирака, сосредоточенная в точке 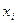, где расположена упругая опора, а 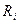- реакция дискретной опоры

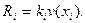
Таким образом, уравнение (8.3) принимает вид

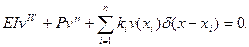(8.15)

Способ записи общего решения такого уравнения изложен в [7]. С этим общим решением следует далее поступать точно так же, как и с решением в форме (8.4).

В. Пусть, наконец, стержень оперт на непрерывное основание и кроме того имеет дискретные опоры.

Решение снова можно получить по методу начальных параметров, выразив на каждом из участков константы 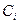(8.4) через параметры решения в начале каждого из участков. Для этого нужно на участке с произвольным номером 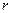записать

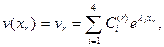
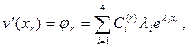
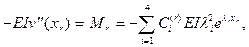(8.16)

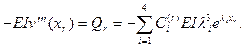
Разрешив эту систему относительно 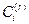, следует затем пройти от левого конца, где известны два параметра из четырех, до правого конца стержня. Подчинив там решение двум оставшимся однородным условиям, мы получим характеристическое уравнение относительно .

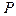При численной реализации этого алгоритма следует иметь в виду, что матрица коэффициентов граничных условий на правом конце может оказаться плохо обусловленной. Поэтому при переходе от левого конца к правому целесообразно использовать метод “прогонки”.

К решению задачи можно подойти и с помощью обобщенных функций.

Соответствующее дифференциальное уравнение будет в отличие от (8.15) иметь вид

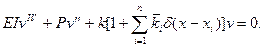(8.17)

Здесь 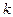- коэффициент упругости непрерывного основания, а 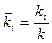- относительная жесткость дискретных опор.

Задачу устойчивости стержня с дискретными опорами можно приближенно решать и энергетическим методом. Для этого в выражение для изменения полной энергии 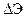следует включить потенциальную энергию упругого основания при работе дискретных опор на изгиб и кручение. В результате выражение, аналогичное (7.20) будет иметь вид

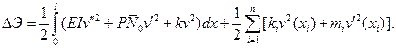(8.18)

Минимизировать функционал (8.18) можно любым из рассмотренных выше методов.

При этом, отыскивая решение в виде ряда

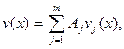(8.19)

следует помнить, что стержень может потерять устойчивость по форме с различным числом полуволн. Поэтому в качестве 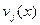необходимо брать первые 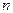членов полной системы функций, удовлетворяющих кинематическим граничным условиям задачи (условиям опирания стержня).