Закритическая деформация стержней

Анализ устойчивости стержней на основе линеаризованных уравнений позволяет найти критические нагрузки, но не позволяет судить ни о характере точки бифуркации, ни о поведении стержня после потери устойчивости.

Чтобы выяснить поведение стержня после потери устойчивости необходимо перейти к нелинейной постановке задачи. Откажемся от ограничения на величину прогибов, но сохраним гипотезу о нерастяжимости оси стержня. Рассмотрим закритическое поведение стержня, изображенного на Рис.9.1.

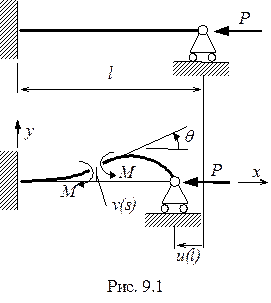
Уравнение равновесия отсеченной части стержня имеет вид

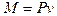. (9.1)

Здесь изгибающий момент внутренних сил

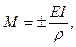(9.2)

где 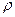- радиус кривизны стержня.

Если координату 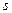отсчитывать по оси стержня от его заделки, то в изображенном на Рис. 9.1 сечении кривизна стержня

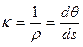(9.3)

отрицательна. Это означает, что формула (9.2) должна быть взята со знаком “минус”.

Уравнение (9.1) с учетом (9.2), (9.3)

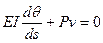(9.4)

содержит две функци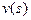и и 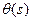, выражающиеся одна через другую.

Если в качестве искомого выбрать функцию v(s), то

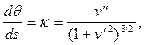
и уравнение (9.4) принимает вид

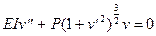. (9.5)

При прогибах стержня, малых настолько, что

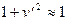, (9.6)

(9.5) принимает рассматривавшийся нами линеаризованный вид

.

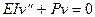Если же условие (9.6) не выполняется, то надо исследовать нелинейное уравнение (9.5) или равносильное ему уравнение, получаемое из (9.4) дифференцированием по s . Если учесть при этом, что

,

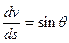то мы получим

(9.7)

Уравнения (9.5), (9.7) удается проинтегрировать в квадратурах. Довольно замысловатую процедуру интегрирования этих уравнений можно посмотреть, например, в [ 2 ], [ 4 ]. Она приводит к табулированным эллиптическим интегралам Эйлера первого рода, то есть в итоге решение фактически оказывается численным.

Можно произвести и непосредственное численное интегрирование уравнения (9.5) при начальных условиях

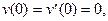
отыскивая путем “пристрелки” такие значения параметра Р, при которых выполнится однородное условие на правом конце .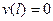

Остановимся на способе построения приближенного решения по методу Ритца. С этой целью запишем функционал, выражающий изменение полной энергии стержня

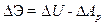
при переходе к искривленному положению равновесия.

Здесь

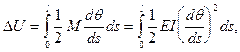
а 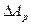записывается как работа силы 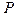на сближении концов стержня за счет его искривления

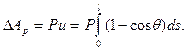
В результате

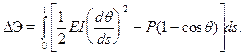(9.8)

Выражение (9.8) по сути аналогично энергетическому критерию в форме Тимошенко. Однако здесь ни на величину 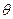, ни, следовательно, на величину прогибов никаких ограничений мы пока не накладывали.

Если ограничиться поиском не бесконечно малых, а малых, но конечных прогибов, то решение в первом приближении можно найти, представив его в виде

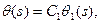(9.9)

где 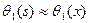- первая собственная функция той же задачи в линеаризованной постановке. Для рассматриваемого примера ( см. Пример П.1.2.)

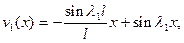(9.10)

где 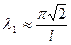- меньший из корней уравнения .

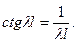Для формы (9.10)

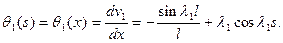
В отличие от линеаризованной постановки, где множитель 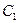остается неопределенным, в нелинейной постановке можно найти множитель 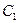при закритической нагрузке. Приняв (9.9), мы фактически рассматриваем поведение системы с одной навязанной ей степенью свободы.

Подставив (9.9) в (9.8), получаем

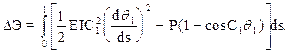(9.11)

Константу 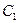найдем из условия

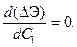(9.12)

Поскольку мы рассматриваем малые прогибы и, следовательно, углы 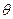, близкие к нулю, для приближенной реализации условия (9.12) разложим 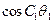в ряд Тейлора в окрестности нуля. Тогда

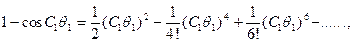(9.13)

и условие (9.12) принимает вид

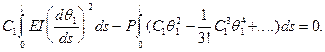(9.14)

Если мы ограничимся в (9.13) только первым членом разложения, то получим известную из линеаризованной постановки формулу

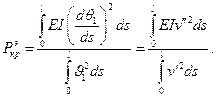
Удерживая и другие члены, получаем

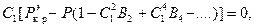(9.15)

где

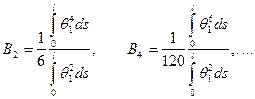(9.16)

Анализ уравнения (9.15) показывает, что при 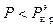есть только одно решение 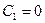, а при 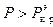возможны и другие вещественные значения 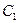. Ограничившись членом 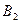, при 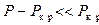имеем

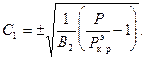(9.17)

Описанный подход носит общий характер и приводит к цели при различных вариантах закрепления и нагружения стержня.

Выясним, насколько сильным является ограничение, обусловленное предположением о малости закритических прогибов. С этой целью оценим максимальные закритические напряжения в поперечном сечении:

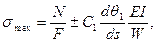(9.18)

где 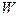- момент сопротивления поперечного сечения.

Распишем выражение для стержня, шарнирно опертого по обоим концам и сжатого силой 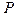, превышающей 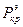на малую величину .

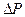Для этого случая

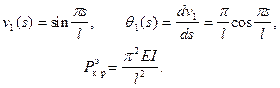
Формула (9.18) дает

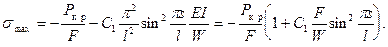(9.19)

По формулам (9.16),(9.17)

.

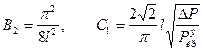Для квадратного поперечного сечения со стороной 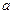имеем 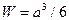, и формула (9.19) дает

.

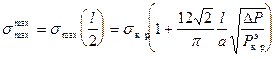Отсюда ясно, что для тонких стержней 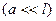даже незначительное превышение критической нагрузки дает резкое увеличение напряжений. К примеру, при

.

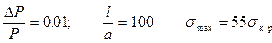Произведенная оценка показывает, что хорошо спроектированные, т.е. достаточно жесткие на изгиб стержни уже при малых закритических прогибах будут разрушаться. Исследование поведения при конечных прогибах целесообразно только для очень гибких стержней.