Метод Релея - Ритца - Тимошенко

Для отыскания приближенного минимума функционала энергии можно использовать метод, известный в строительной механике под названием метода Ритца-Тимошенко. Этот метод впервые был применен Релеем для решения задач колебаний, сводившихся так же как и задачи устойчивости к задачам на собственные значения. Будем в дальнейшем называть его методом Релея.

Функция прогиба стержня ищется в виде ряда

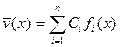, (7.38)

где 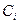- искомые константы, а 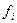- функции, выбранные заранее так, чтобы перемещения 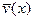были возможными, то есть непрерывными и подчиняющимися кинематическим граничным условиям, в данном случае - однородным.

Воспользуемся энергетическим критерием в форме Брайана.

Подставим ряд в выражение (7.20) и, выполнив операции дифференцирования и интегрирования, получим алгебраическую зависимость

DЭ = DЭ 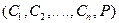(7.40)

Условия стационарности этого функционала как функции n переменных 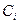имеет вид

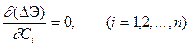(7.41)

Система (7.41) всегда однородна и линейна относительно 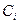. В матричной форме записи эта система для изолированного стержня имеет вид

AV+ 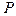BV =0, (7.42)

где А , В - ( 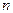´ 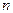) матрицы с коэффициентами

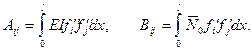(7.43)

Таким образом, мы пришли к задаче на собственные значения для матриц.

Условия для определения собственных значений

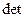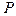( A + B) = 0 . (7.44)

Наименьший из корней 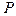уравнения (7.44) будет приближенным 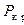, причем при любом конечном n это значение будет выше или по крайней мере не ниже точного. Этот факт легко объяснить. Ограничившись некоторым n , мы как бы навязываем стержню конечное число степеней свободы, делая его тем самым жестче рассматриваемого.

Если система функций - 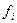полная, то при n® ¥ мы придем к точному решению, удовлетворяющему и статическим граничных условиям, кроме принятых кинематических. Если среди предложенных нами есть и точное решение задачи, то мы в точности найдем его, а множители при остальных функциях обнулятся.

Если система функций 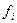такова, что каждая из систем функций 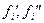оказывается ортогональной, то система (7.42) пр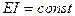и и 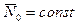распадается на независимые уравнения и дает

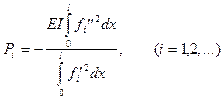(7.45)

то есть, для 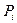мы получаем формулу. Во всех остальных случаях процесс поиска 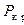, при не слишком малых 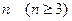остается численным.