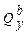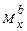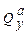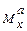Балка на упругом основании
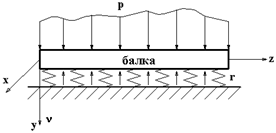 Рис.10.1
Рис.10.1
| В инженерной практике встречаются балки, лежащие на сплошном упругом основании. Это ленточные фундаменты зданий, фундаменты плотин, ж/д шпалы и др. Расчет таких балок осложняется тем, что реакция оснований « 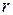 » »
|
зависит от прогибов « 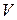 » балки, а прогибы зависят от реакции основания. Для решения задачи необходимо знать закон, связывающий реакцию основания с осадкой (прогибом) основания. Наиболее распространенной является гипотеза Винклера
» балки, а прогибы зависят от реакции основания. Для решения задачи необходимо знать закон, связывающий реакцию основания с осадкой (прогибом) основания. Наиболее распространенной является гипотеза Винклера
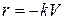 (1)
(1)
Обозначим
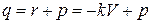 (2)
(2)
Здесь: 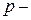 внешняя погонная нагрузка;
внешняя погонная нагрузка; 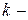 коэффициент постели, приводится в справочниках для различных грунтов;
коэффициент постели, приводится в справочниках для различных грунтов; 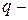 суммарная погонная нагрузка, действующая на балку.
суммарная погонная нагрузка, действующая на балку.
Для решения задачи используем известное дифференциальное уравнение изогнутой оси бруса
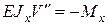 (3)
(3)
Обычно 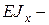 изгибная жесткость балки, считается константой. Ранее получены дифференциальные зависимости (1.7)
изгибная жесткость балки, считается константой. Ранее получены дифференциальные зависимости (1.7)
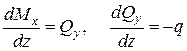 (4)
(4)
Дифференцируя один раз (3) с учетом (4) получим
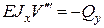 (5)
(5)
Дифференцируя (5) с учетом (4) найдем
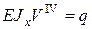 (6)
(6)
Подставим (2) в (6)
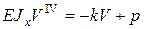 (7)
(7)
Обозначим 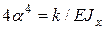
Тогда уравнение (7) примет вид
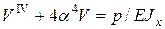 (10.1)
(10.1)
Это дифференциальное уравнение балки на упругом основании.
I. Бесконечно-длинная балка, загруженная локальной силой
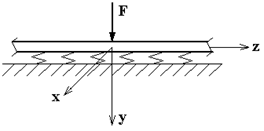 Рис.10.2
Рис.10.2
| Задача симметрична относительно силы 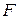 , поэтому рассмотрим лишь ее правую половину. Начало координат поместим под силой , поэтому рассмотрим лишь ее правую половину. Начало координат поместим под силой 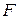 . Здесь . Здесь 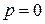 и уравнение (10.1) примет вид и уравнение (10.1) примет вид
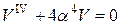 (9) (9)
|
Общий интеграл этого уравнения приводится в справочниках
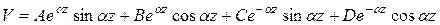 (10.2)
(10.2)
Здесь: 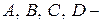 неизвестные const, которые определяются из граничных условий задачи:
неизвестные const, которые определяются из граничных условий задачи:
1. При 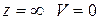 . Подставим это в (10.2)
. Подставим это в (10.2)
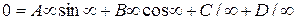
Это может быть, когда 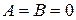 . Уравнение (10.2) с учетом этого упростится
. Уравнение (10.2) с учетом этого упростится
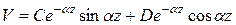 (10.3)
(10.3)
2. Ввиду симметрии прогибов: при 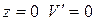 . Дифференцируем (10.3), получим
. Дифференцируем (10.3), получим
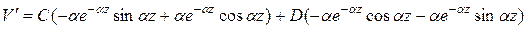
Подставляем 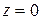 и
и 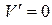 найдем
найдем
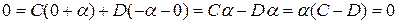
Отсюда следует, что 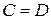 и уравнение (10.3) еще упростится
и уравнение (10.3) еще упростится
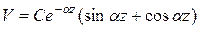 (10)
(10)
3. Правило проверки эпюр 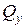 гласит: при движении вдоль эпюры
гласит: при движении вдоль эпюры 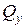 справа – налево скачки на эпюре должны равняться по величине и по направлению локальным силам, приложенным в этих сечениях балки. В нашем случае Эп.
справа – налево скачки на эпюре должны равняться по величине и по направлению локальным силам, приложенным в этих сечениях балки. В нашем случае Эп. 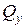 в окрестности силы
в окрестности силы 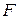 с учетом симметрии задачи должна иметь вид (рис. 10.3):
с учетом симметрии задачи должна иметь вид (рис. 10.3):
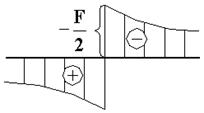 Рис.10.3
Рис.10.3
| Отсюда при 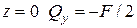 . Подставим это в (5), получим . Подставим это в (5), получим
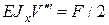 при при 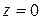 (11)
Надо найти (11)
Надо найти 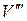 от (10) последовательным дифференцированием от (10) последовательным дифференцированием
|
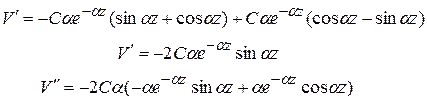
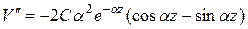 (12)
(12)
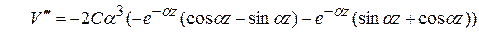
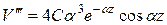 (13)
(13)
Подставим (13) в (11) найдем
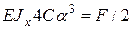 ,
,
откуда
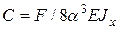 (14)
(14)
Подставим (14) в (10), получим прогибы балки
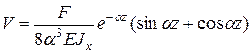 (10.4)
(10.4)
Подставим 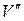 по (12) и С по (14) в (3), получим формулу для изгибающих моментов в балке
по (12) и С по (14) в (3), получим формулу для изгибающих моментов в балке
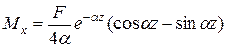 (10.5)
(10.5)
Подставим 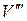 из (13) и С по (14) в (5), получим формулу для поперечных сил в балке
из (13) и С по (14) в (5), получим формулу для поперечных сил в балке
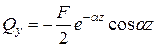 (10.6)
(10.6)
По формулам (10.4)-(10.6) можно построить эпюры, примерный вид которых показан ниже.
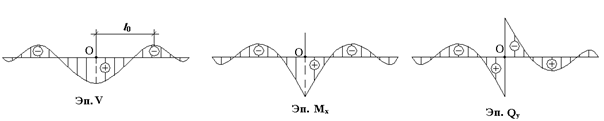
Рис.10.4
Эпюры 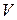 и
и 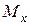 симметричны относительно т.О, а эпюра
симметричны относительно т.О, а эпюра 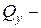 обратносимметрична. Эпюры представляют собой затухающие функции с увеличением
обратносимметрична. Эпюры представляют собой затухающие функции с увеличением 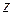 .
.
Обозначим 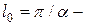 длина полуволны. Расчеты показали, что при
длина полуволны. Расчеты показали, что при 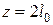
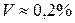 от прогиба под силой
от прогиба под силой 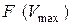 , при
, при 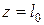
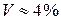 от
от 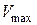 . Поэтому, полученными формулами можно пользоваться и для балок конечной длины, если их длина
. Поэтому, полученными формулами можно пользоваться и для балок конечной длины, если их длина 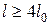 и даже при
и даже при 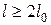 . Для более коротких балок ошибки будут значительны.
. Для более коротких балок ошибки будут значительны.
II. Полубесконечная балка на упругом основании
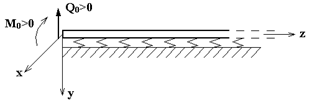 Рис.10.5
Рис.10.5
| Балка загружена при 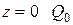 и и 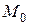 . Здесь . Здесь 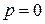 и для решения задачи можно использовать уравнение (9), общее решение которого дано (10.2). и для решения задачи можно использовать уравнение (9), общее решение которого дано (10.2).
|
Граничное условие: при 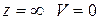 дает
дает 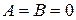 , что приводит к уравнению (10.3)
, что приводит к уравнению (10.3)
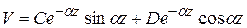 (15)
(15)
Для определения const С и D есть два граничных условия
1. при 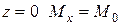 ; с учетом (3)
; с учетом (3) 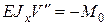 (16)
(16)
2. при 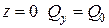 ; с учетом (5)
; с учетом (5) 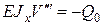 (17)
(17)
Последовательным дифференцированием (15) найдем
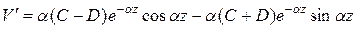 (18)
(18)
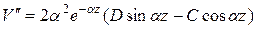 (19)
(19)
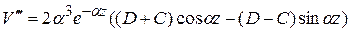 (20)
(20)
Подставим 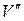 из (19) при
из (19) при 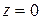 в (16) получим
в (16) получим
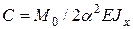 (21)
(21)
Подставим 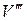 по (20) при
по (20) при 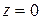 в (17) найдем
в (17) найдем
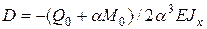 (22)
(22)
Подставляя в (3) 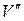 из (19) и найденные значения С и D из (21)-(22), после преобразований получим
из (19) и найденные значения С и D из (21)-(22), после преобразований получим
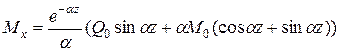 (10.7)
(10.7)
Подстановка 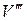 по (20), С и D в (5) дает
по (20), С и D в (5) дает
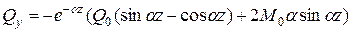 (10.8)
(10.8)
В формулы (10.7) и (10.8) 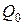 и
и 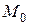 подставлять со своими знаками, положительные их направления на левом торце балки показаны на рис. 10.5.
подставлять со своими знаками, положительные их направления на левом торце балки показаны на рис. 10.5.
III. Расчет короткой балки методом
последовательных приближений
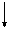
   
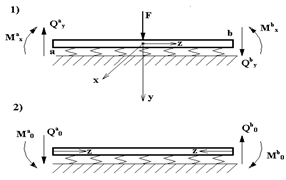 |
Рис.10.6
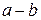 , загруженную силой
, загруженную силой 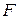 , под которой поместим начало координат (рис.10.6). Представим ее беско-нечно длинной в оба конца и по формулам (10.5) и (10.6) построим эпюры
, под которой поместим начало координат (рис.10.6). Представим ее беско-нечно длинной в оба конца и по формулам (10.5) и (10.6) построим эпюры 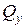 и
и 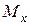 на участке
на участке 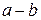 . Пусть в сечениях «а» и «b» эти внутренние силовые факторы (ВСФ)
. Пусть в сечениях «а» и «b» эти внутренние силовые факторы (ВСФ)
оказались положительными, их направления 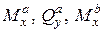 и
и 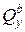 показаны на рис.10.6. Сечения «а» и «b» концы балки, поэтому ВСФ в них должны быть равны нулю. Этого можно добиться, приложив в этих сечениях внешние
показаны на рис.10.6. Сечения «а» и «b» концы балки, поэтому ВСФ в них должны быть равны нулю. Этого можно добиться, приложив в этих сечениях внешние 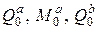 и
и 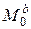 , равные и противоположно направленные ВСФ (рис.10.6). Балку на рис.2) надо рассчитать дважды: 1) от
, равные и противоположно направленные ВСФ (рис.10.6). Балку на рис.2) надо рассчитать дважды: 1) от 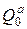 и
и 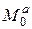 при оси
при оси 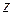 вправо; 2) от
вправо; 2) от 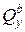 и
и 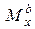 при оси
при оси 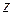 влево по формулам (10.7) и (10.8) полубесконечной балки и построить по ним эпюры. Итоговые значения
влево по формулам (10.7) и (10.8) полубесконечной балки и построить по ним эпюры. Итоговые значения 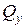 и
и 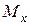 получим, суммируя эпюры от вышеуказанных трех расчетов. При очень короткой балке на итоговых эпюрах
получим, суммируя эпюры от вышеуказанных трех расчетов. При очень короткой балке на итоговых эпюрах 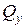 и
и 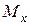 в сечениях «а» и «b» балки ВСФ могут оказаться значительными (а должны быть равны нулю). Поэтому еще раз надо повторить два расчета балки по схеме рис.2, приложив на торцах балки внешние
в сечениях «а» и «b» балки ВСФ могут оказаться значительными (а должны быть равны нулю). Поэтому еще раз надо повторить два расчета балки по схеме рис.2, приложив на торцах балки внешние 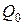 и
и 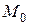 , равные и противоположно направленные ВСФ итоговых эпюр. Полученные эпюры
, равные и противоположно направленные ВСФ итоговых эпюр. Полученные эпюры 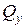 и
и 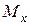 суммируем с имеющимися итоговыми. Отличие
суммируем с имеющимися итоговыми. Отличие 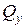 и
и 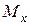 от нулевых значений на торцах балки уменьшится. На практике обычно бывает достаточно одного или двух приближений для получения приемлемых результатов.
от нулевых значений на торцах балки уменьшится. На практике обычно бывает достаточно одного или двух приближений для получения приемлемых результатов.
IV. Расчет балок по линиям влияния
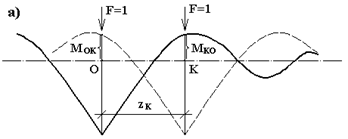 Рис.10.7
Рис.10.7
| Бесконечная длинная балка на упругом основании показана на рис.10.7 как горизонтальная штрих-пунктирная линия. Пусть на нее в т.О действует сила 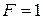 . По (10.5) для балки . По (10.5) для балки
|
можно построить эпюру 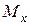 , которая на рис.10.7 показана сплошной линией. Величина
, которая на рис.10.7 показана сплошной линией. Величина 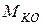 определяет
определяет 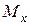 в произвольной т.K (с координатой
в произвольной т.K (с координатой 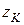 ) от силы
) от силы 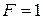 приложенной в т.О. Если силу
приложенной в т.О. Если силу 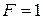 приложить в т.K, то эпюру
приложить в т.K, то эпюру 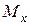 можно изобразить пунктирной линией. Величина
можно изобразить пунктирной линией. Величина 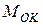 определяет
определяет 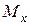 в т.О от силы
в т.О от силы 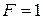 , приложенной в т.K. Ввиду симметрии эпюры
, приложенной в т.K. Ввиду симметрии эпюры 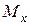 очевидно, что
очевидно, что 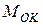 =
= 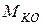 . Этот вывод справедлив для любого положения силы
. Этот вывод справедлив для любого положения силы 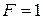 , т.е. сплошная линия изображает закон изменения
, т.е. сплошная линия изображает закон изменения 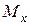 в т.О от движения силы
в т.О от движения силы 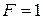 вдоль балки. Сплошную линию на рис.10.7 называют линией влияния.
вдоль балки. Сплошную линию на рис.10.7 называют линией влияния.
Пусть на балку действует произвольная нагрузка (рис.10.8). В произвольном сечении (т.О) найти 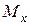 от этой нагрузки.
от этой нагрузки.
В интересующем нас сечении (т.О) расположим начало координат и строим эпюру 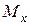 от действия в этой точке силы
от действия в этой точке силы 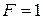 . Получим линию влияния. Под силами
. Получим линию влияния. Под силами 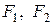 и
и 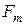 определяем с учетом знаков
определяем с учетом знаков 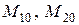 и
и 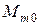 . В сечении т.О изгибающий момент
. В сечении т.О изгибающий момент 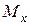 найдем алгебраическим суммированием
найдем алгебраическим суммированием
|
|
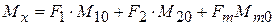 (23)
(23)
      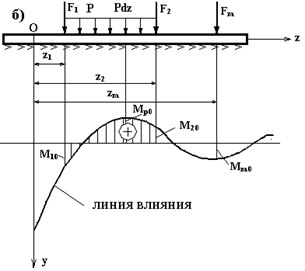 Рис.10.8
Рис.10.8
| Если участок балки нагружен внешней погонной нагрузкой 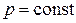 (рис.10.8), то разбивая ее на малые силы (рис.10.8), то разбивая ее на малые силы 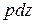 и определяя от них на линии влияния и определяя от них на линии влияния 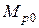 , по аналогии с (23) найдем , по аналогии с (23) найдем
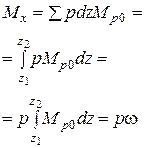 (24) (24)
|
Здесь 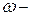 заштрихованная площадь линии влияния под нагрузкой
заштрихованная площадь линии влияния под нагрузкой 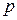 (определяется с учетом знаков). В справочниках приводятся таблицы для вычисления
(определяется с учетом знаков). В справочниках приводятся таблицы для вычисления 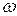 . Можно использовать численные методы при помощи ЭВМ.
. Можно использовать численные методы при помощи ЭВМ.
Аналогично можно построить линию влияния прогибов V и по ней определять прогибы в любом сечении балки.
Эпюра 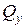 обратносимметрична относительно
обратносимметрична относительно 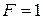 , поэтому
, поэтому 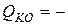
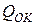 , и линия влияния
, и линия влияния 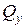 отличается знаком от самой эпюры
отличается знаком от самой эпюры 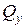 . Для коротких балок можно уточнить решение, используя вышеизложенный метод последовательных приближений.
. Для коротких балок можно уточнить решение, используя вышеизложенный метод последовательных приближений.
| <== предыдущая лекция | | | следующая лекция ==> |
| | | Основные уравнения механики деформируемого твердого тела (МДТТ) |
Дата добавления: 2016-10-18; просмотров: 4486;