СИСТЕМА УРАВНЕНИЙ ЭЙЛЕРА
Нестационарные уравнения Эйлера для трехмерного течения сжимаемого газа в консервативной и безразмерной форме в декартовой системе координат (x,y,z) имеют вид [29]:
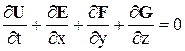 ,
,
где 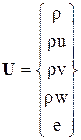 ;
; 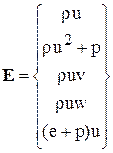 ;
; 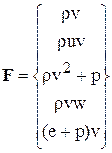 ;
; 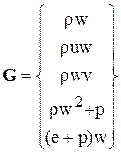 ,
,
где t – время, r – плотность, (u, v, w) – составляющие вектора скорости V соответственно в направлениях (x, y, z), p - давление, e - полная энергия единицы объема газа, которая для совершенного газа может быть представлена в виде 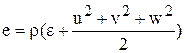 , где e – внутренняя энергия газа.
, где e – внутренняя энергия газа.
 Безразмерные переменные определены через размерные, обозначенные штрихом, следующим образом:
Безразмерные переменные определены через размерные, обозначенные штрихом, следующим образом:
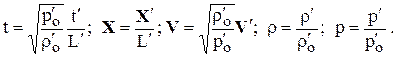
Нижний индекс «О» - значение параметра в невозмущенном потоке. Здесь 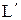 - характерный размер; X=(x, y, z); V=(u, v, w).
- характерный размер; X=(x, y, z); V=(u, v, w).
Использование декартовой системы координат для адекватного описания течений со сложной топологией при решении задач конечно-разностными методами представляется сложным по двум причинам: необходимы интерполяционные процедуры для получения граничных условий; возникают трудности в описании расчетной сетки, так как расчетная сетка не является прямоугольной. Перейдем к произвольной криволинейной системе координат [30]. Равномерную сетку для разностной аппроксимации исходных уравнений будем задавать в системе координат:
t=t; x=x(x, y, z); h=h(x, y, z); z=z(x, y, z).
Использование обобщенного преобразования позволяет сохранить строго консервативную форму уравнений. Уравнения принимают вид:
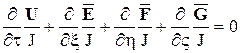
Здесь 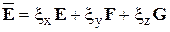 ;
; 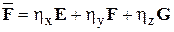 ;
; 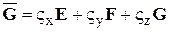 .
.
Коэффициенты матрицы преобразования могут быть вычислены по следующим формулам:
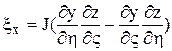 ;
; 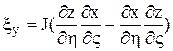 ;
; 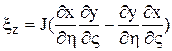 ;
;
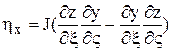 ;
; 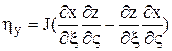 ;
; 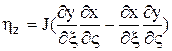 ;
;
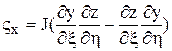 ;
; 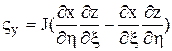 ;
; 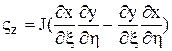 ,
,
где J – есть якобиан преобразования, который определяется по формуле
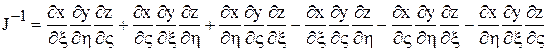 .
.
Использование обобщенного преобразования позволяет построить равномерную сетку в виде единичного куба. Коэффициенты матрицы преобразования могут быть вычислены аналитически, если преобразование задается алгебраически, либо с использованием разностных формул в соответствии с уравнениями, если задано распределение узлов в физической области расчета. Если ввести контрвариантные компоненты вектора скорости
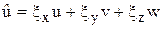 ;
; 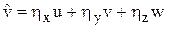 ;
; 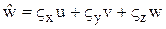 ,
,
то вектора 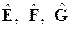 можно представить в виде
можно представить в виде
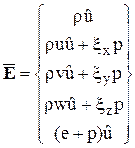 ;
; 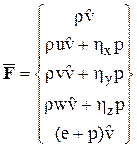 ;
; 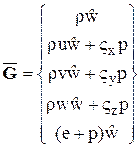 .
.
Математическая постановка задачи остается неполной, если не заданы дополняющие систему дифференциальных уравнений начальные и граничные условия. Для правильной постановки задачи необходимо знать тип системы уравнений движения. Задание начальных условий должно рассматриваться применительно к конкретной задаче. Остановимся на задании граничных условий. Граничные условия на поверхности тела для невязкого газа заключаются в условии непротекания: 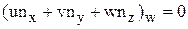 . Индекс «w» означает, что значение газодинамической функции или параметра взято на границе;
. Индекс «w» означает, что значение газодинамической функции или параметра взято на границе; 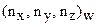 - нормаль к границе.
- нормаль к границе.
На внешней границе задание граничных условий для сверхзвуковых течений связано с численным методом решения:
1 - расчет без выделения головного скачка уплотнения;
2 - расчет с выделением головного скачка уплотнения.
В первом случае на внешней границе, которая должна быть размещена в невозмущенной области течения, должны поддерживаться условия набегающего потока. В этом случае необходимо следить за тем, чтобы выбор внешней границы не влиял на результаты расчета.
Во втором случае для задания граничных условий должны привлекаться соотношения на сильном разрыве. Для совершенного газа это соотношения Ренкина - Гюгонио [29]:
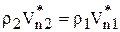 ,
, 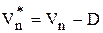 ,
, 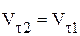 ,
,
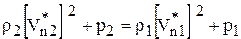 ,
, 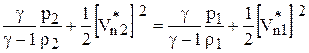 .
.
Здесь 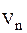 и
и 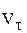 - проекции вектора скорости V на нормаль к поверхности ударной волны и на плоскость, касательную к ней, D - скорость перемещения ударной волны. Индекс «1» относится к параметрам невозмущенного потока, индекс «2» - к параметрам за ударной волной. С учетом проведенного обезразмеривания получим
- проекции вектора скорости V на нормаль к поверхности ударной волны и на плоскость, касательную к ней, D - скорость перемещения ударной волны. Индекс «1» относится к параметрам невозмущенного потока, индекс «2» - к параметрам за ударной волной. С учетом проведенного обезразмеривания получим 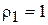 ,
, 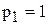 ,
, 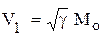 , где
, где 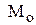 - число Маха в набегающем потоке.
- число Маха в набегающем потоке.
Следует упомянуть об условиях симметрии, если таковая присутствует в постановке задачи.
Коническими течениями называются такие течения, параметры которых остаются постоянными вдоль лучей, выходящих из некоторой точки О, называемой центром коничности (рис.2.1). При рассмотрении обтекания тел конической формы предполагается, что течение обладает конической симметрией - параметры течения постоянны вдоль лучей, исходящих из вершины тела – точки О.
Система уравнений Эйлера для конических течений получается введением переменных (x,h,V) в следующем виде: 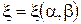 ,
, 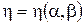 ,
, 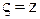 , где
, где 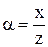 ,
, 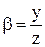 и при предположении коничности течения, которое математически определяется условием
и при предположении коничности течения, которое математически определяется условием 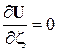 , в сечении
, в сечении 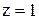 принимает вид
принимает вид
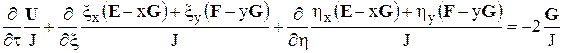 .
.
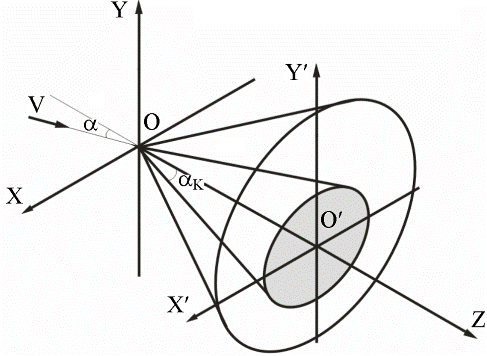
Рис.2.1
Коэффициенты матрицы преобразования и якобиан определяются следующими формулами:
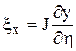 ,
, 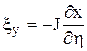 ,
, 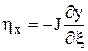 ,
, 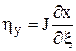 ,
, 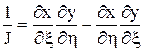 .
.
Дата добавления: 2016-09-06; просмотров: 3985;











