Скорость распространения малых возмущений

В газах

Скорость распространения малых возмущений в идеальном газе.Для выяснения особенностей движения газа важно сравнить скорость его течения с характерной для идеального газа и зависящей от его термодинамического состояния величиной – скоростью распространения малых возмущений по газу или, что всё равно, скорость распространения звука.

Рассмотрим баротропный поток идеального газа, параллельного оси х, течение нестационарное, давление р, плотность r и температура Т функции только х и t , массовыми силами пренебрегаем.

Рассмотрим для простоты одномерное течение. Одномерным называют течения, у которых все физические параметры являются функцией только одной пространственной координаты и времени. Наиболее важным является прямолинейное одномерное течение газа.

Простейшей схемой движущегося рабочего тела является идеальная жидкость или газ. Принимая эту схему, отвлекаются от наличия внутреннего трения, считая, что по площадкам соприкасания двух друг относительно друга движущихся объемов действуют лишь нормальные к площадке силы давления и полностью отсутствуют лежащие в плоскости площадки касательные силы трения. При этом уравнения переходят в уравнения движения невязкого, нетеплопроводного газа.

Уравнение Эйлера и уравнение неразрывности сводятся к нелинейной системе дифференциальных уравнений первого порядка в частных производных:

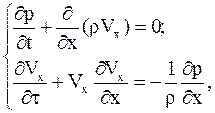(1.43)

с тремя неизвестными функциями V_x , p, r.

Чтобы система была определенной, необходимо добавить еще уравнение связи между r и р или, в более общем случае, уравнение Клайперона и уравнение баланса энергии.

Задача о распространении малых возмущений в газе формируется следующим образом: в покоящемся идеальном газе создаются малые возмущения скоростей, причем возникающее вследствие этого движение является одномерным, параллельным оси х баротропным, зависящем от координаты х и t.

Пусть V, p и r - скорость, давление и плотность возмущенного движения; р₀ и r₀ – давление и плотность покоящегося газа; V' , p' , r' – малые возмущения скорости, давления и плотности. Тогда

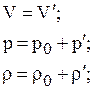(1.44)

Подставив значения (1.44) в систему (1.43) и пренебрегая произведениями малых величин и их производных по координатам как малыми высших порядков (с точностью до малых величин первого порядка малости)

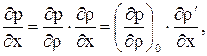
получим:

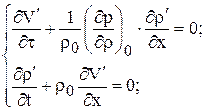(1.45)

Система (1.45) является линеаризованной по сравнению с (1.43) . Замечая, что величина 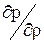существенно положительна, т.к. плотность газа растет с давлением, обозначим 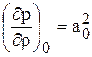, тогда (1.45) перепишем в виде:

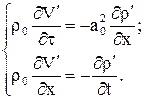(1.46)

Систему уравнений (1.46) сведем к одному уравнению. Дифференцируя обе части первого уравнения системы (1.46) по времени t, а второго – по х, умножая обе части второго уравнения на а₀² и вычитая его почленно из первого, получим линейное уравнение гиперболического типа (одномерное волновое уравнение):

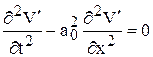. (1.47)

Его решение:

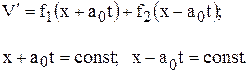
Общая для обеих волн скорость а₀ называется скоростью распространения малых возмущений в газе и равна:

.

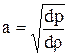Аналогичное уравнение можно получить для определения r':

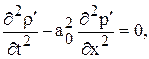
но

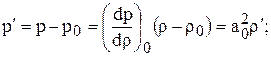
а для р'

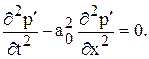
Общее решение любого из этих уравнений, как известно, можно представить в виде суммы двух произвольных функций:

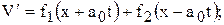(1.48)

вид функций f₁ и f₂ зависит от начальных условий задачи.

Введем новые координаты x₁ и x₂ , связанные со старыми при помощи равенств:

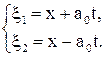
Такое преобразование имеет простой кинематический смысл. Ось координат О₁x₁ расположена вдоль оси О_х и движется поступательно в сторону отрицательного направления оси О_х со скоростью а_{0 ,} ось О₂x₂ движется поступательно в сторону положительного направления оси О_х с той же скоростью.

Решение (1.48) принимает при этом вид:

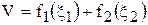. (1.49)

Рассмотрим каждое слагаемое по отдельности, т.е. следующих два частных решения уравнения (1.47):

Функция f₁(x₁) представляет в подвижной системе O₁x₁ не зависящее от времени распространение возмущений скорости. Эта фиксированная форма одномерного возмущения, согласно первому из равенств (1.49) движется как одно целое вдоль отрицательного направления оси ох со скоростью а₀ . Аналогична эта функция f₂(x₂). Полагая, что в этих решениях x₁ = const или x₂ = const, получим две системы плоских волн:

(1.50)

представляющих две движущихся в противоположные стороны со скоростью а₀ перпендикулярные оси ох плоскости, каждая из которых несет постоянные, заданные начальными условиями значения возмущений скорости, давления, плотности или температуры, такие волны называются простыми.

Общее решение уравнения (1.47), а следовательно, и аналогичных уравнений для возмущения давления и плотности складывается из решений, соответствующих двум распространяющимся в противоположные стороны простым волнам. Геометрически решение можно интерпретировать, как наличие в плоскости (х, t) двух семейств прямых (1.50) с угловыми коэффициентами, вдоль каждой из прямых сохраняются постоянные значения заданных начальными условиями возмущений скорости или других параметров. Эти два семейства представляют два семейства характеристик волнового уравнения (1.47).

Общая для обеих волн скорость а₀ называется скоростью распространения малых возмущений в газе и определяется согласно (1.45), формулой

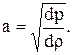(1.51)

Широко наблюдаемое явление распространения малых возмущений в жидкостях и газах - распространение звука, заключающееся в распространении волн слабого сжатия и разряжения. Поэтому величину а называют скоростью звука.

Если процесс распространения звука изотермический, учитывая, что при этом 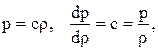то изотермическая скорость звука будет

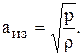
Если предположить, что процесс распространения звука происходит так быстро, что можно пренебречь влиянием отвода тепла и процесс становится адиабатическим 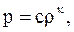тогда

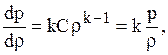
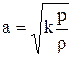(получено Лапласом) (1.52)

Под скоростью звука в дальнейшем подразумеваем адиабатическую скорость (12)

Используя формулу Клайперона, перепишем (1.52)

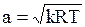. (1.53)

Отсюда следует, что скорость звука в совершенном газе зависит только от (абсолютной) температуры и физических свойств газа.

Для воздуха 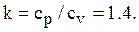Используя данные о стандартной атмосфере, можно получить скорость звука на различной высоте.

Критическая скорость.В зависимости от того, больше или меньше скорости звука скорость движения частиц, принципиально разными будут и происходящие в среде явления.

Например, из баллона большей емкости происходит истечение газа в камеру. Если вначале разность давлений в баллоне и в камере невелика, скорость течения не превосходит скорость звука. При понижении давления в камере скорость истечения увеличивается. Создаваемые в камере возмущения давления будут распространяться против течения из камеры через патрубок, в баллон до тех пор, пока скорость в выходном сечении трубопровода не достигнет скорости звука. После этого возмущения давления не смогут проникать в баллон, т.к. они будут сноситься потоком, имеющим ту же скорость, что и скорость распространения возмущений в газе. Продолжающееся понижение давления в камере не отразится на явлении истечения, скорость которого будет оставаться постоянной и равной скорости звука в выходном сечении патрубка – произойдет “ запирание ” потока.

Если в потоке газа скорость V равна местной скорости звука, то такая скорость газа V = V_кр называется критической. Давление p, плотность r и температура T примут также критические значения p_кр , r_кр , Т_кр .

Отношение скорости V движения газа в данной точке потока к соответствующей этой точке местной скорости звука называется числом Маха (M):

.

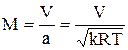При M < 1 – поток дозвуковой, при M > 1 – сверхзвуковой. Отношение скорости потока в данной точке к одинаковой для всего потока критической скорости a_кр называется скоростным коэффициентом (l):

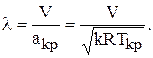
Параметры неподвижного потока (например, в баллоне) называют параметрами заторможенного потока.

Эти понятия широко используются при описании газодинамических процессов в камере РДТТ.

До- и сверхзвуковое течение.Качественное различие между до- и сверхзвуковым течениями иллюстрируется при рассмотрении точечного источника возмущения – тела А, движущегося со скоростью V в покоящемся газе. Возмущения распространяются в виде сферических волн со скоростью звука а. При дозвуковой скорости источника движение сопровождается сигналами, посланными вперед со скоростью, равной скорости звука (рис.1.7, t – интервал времени). При этом область возмущения опережает тело, и поток изменяется еще до того, когда частицы газа придут в соприкосновение с телом.

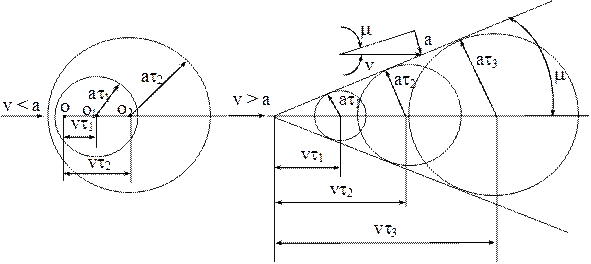
Рис.1.7

При сверхзвуковой скорости движения источника возмущения не будут обгонять посланные им сигналы – сферические волны будут находиться внутри конуса, огибающего сферы возмущений. Конус называется конусом возмущения (конусом Маха). Вокруг конуса поток является невозмущенным – зона “молчания”. На конусе, или линиях возмущения, служащих границей, разделяющий поток на возмущенную или невозмущенную области, возмущения расположены наиболее плотно, т.к. все звуковые волны находятся на этом конусе в одной и той же фазе – фазе уплотнения. Также возмущенные области – конические или плоские волны, ограниченные прямыми линиями Маха – называются простыми волнами сжатия, или волнами Маха.

Угол m наклона образующей конической волны или линии возмущения определяется из условия (см. рис.1.7), что 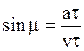откуда .

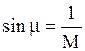Угол m называется углом возмущения или углом Маха. Сверхзвуковой поток сносит все звуковые возмущения вниз по потоку, ограничивая их распространение конусом, или линиями возмущения, наклоненными под углом m. Фронт простой волны распространяется с той же звуковой скоростью, что и сферическая волна. Поэтому проекция вектора скорости набегающего потока на нормаль к фронту волны равна скорости звука.