ТОРМОЖЕНИЕ СВЕРХЗВУКОВОГО ПОТОКА.

СКАЧКИ УПЛОТНЕНИЯ

Физическая природа возникновения скачков уплотнения.Особенностью сверхзвуковых газовых потоков является то, что в них при торможении образуются поверхности разрыва, при прохождении через которые параметры газа меняются скачкообразно: скорость резко уменьшается, а давление, температура и плотность возрастают. Такие поверхности разрыва, перемещающиеся относительно газовой среды, иногда называются ударными волнами, а неподвижные поверхности разрыва – стационарными ударными волнами или скачками уплотнения. В дальнейшем будем рассматривать в основном «скачки уплотнения».

В общем случае скачок уплотнения имеет криволинейную форму. На рис.1.8 (а, б, в) показан присоединенный криволинейный скачек, отсоединенный криволинейный и присоединенный прямолинейный скачки.

а б в

Рис.1.8

На рис. (б) видно, что поверхности скачков уплотнения могут быть ориентированы по направлению нормали к вектору скорости набегающего потока или наклонены под некоторым углом, отличным от прямого. В первом случае скачек называется прямым, а во втором – косым. Очевидно, присоединенный криволинейный скачок можно рассматривать как совокупность косых скачков, а отсоединенный скачок – состоящим из прямого скачка и системы косых скачков.

Образование скачков уплотнения обусловлено специфическим характером распространения возмущений в сверхзвуковом потоке. Возмущение – это местное уплотнение, сопровождающееся повышением давления.

Как показано выше, при сверхзвуковой скорости потока (v > a) образуется конус возмущения (конус Маха). На плоскости огибающими круговых волн будут линии возмущения (линии Маха). На конусе, или линиях возмущения, служащих границей, разделяющей поток на возмущенную и невозмущенную области, возмущения расположены наиболее плотно, т.к. все звуковые волны находятся на этом конусе в одной и той же фазе колебания – фазе уплотнения. Такие возмущенные области (конические или плоские волны) называются простыми волнами сжатия или волнами Маха:

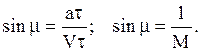
Фронт простой волны распространяется с той же звуковой скоростью, что и сферическая волна. Поэтому проекция вектора скорости набегающего потока на нормаль к фронту волны равна скорости звука.

В простой волне сжатия, как и в звуковой, параметры газа изменяются на бесконечно малую величину.

В возмущенной области скорость практически остается такой, как и в невозмущенном. Поэтому такую простую волну можно рассматривать как скачок уплотнения бесконечно малой интенсивности и практически при переходе через нее параметры не изменяются. Поэтому ее называют слабой волной, а ее фронт – линией слабых возмущений.

Предполагают, что образование скачка конечной интенсивности связано со сложением простых волн сжатия и, как результат, их взаимным усилением. Пусть поток движется вдоль стенки. Создадим искусственное местное повышение давления в точке А, повернув поток на бесконечно малый угол db.

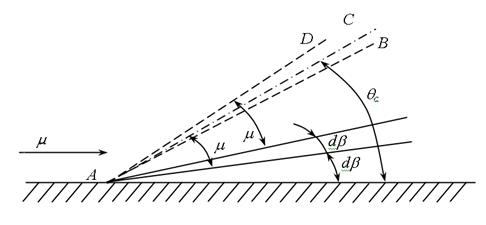
Рис.1.9

Это вызовет простую волну сжатия АВ, наклоненную к поверхности на угол m. Если осуществить дополнительный малый поворот на угол db, то образуется новая простая волна АС. Однако в сверхзвуковом потоке, как было показано, волны не могут распространяться вверх по течению, поэтому волна АС будет сноситься вниз по потоку до совпадения с первой. При этом образуется более интенсивная волна.

Образующийся таким образом скачок уплотнения конечной интенсивности имеет скорость распространения, большую, чем скорость звука, с которой движется простая волна. Поэтому этот скачок отклоняется от простой волны АВ влево (АД) и занимает положение, при котором он удерживается в равновесии, т.к. скорость его распространения будет равна составляющей скорости набегающего потока по нормали к фронту скачка Vsinq_c, тогда q_с – угол наклона скачка. Отсюда следует, что угол наклона скачка уплотнения конечной интенсивности больше угла наклона линии (конуса) возмущения, т.е. q_с > m.

Возникающий в реальных условиях скачок уплотнения характеризуется некоторой толщиной, изменение параметров происходит не мгновенно, а с течением времени. Но толщина скачка весьма мала и имеет порядок длины свободного пробега молекул. Поэтому в идеальной среде этой толщиной пренебрегают и скачок представляют в виде поверхности разрыва непрерывности для параметров газа, полагая, что изменение этих параметров происходит мгновенно.

Пусть в некоторой области произошло изменение давления, и волна получила плавную форму 1АВ2 (рис.1.10). На отдельных бесконечно узких участках волны величина давления возрастает незначительно, поэтому распространение такой волны происходит со скоростью звука. В области высоких сжатий (А) температура выше, чем в области меньших сжатий (В), поэтому вершина волны движется быстрее.

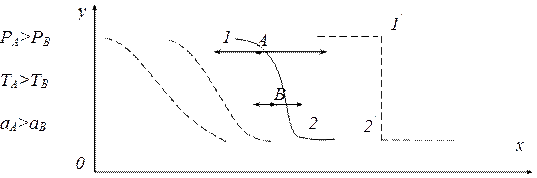
Рис.1.10.

К точке О волна распространяется как волна разряжения, в сторону высоких давлений – как сжатия. Волна сжатия приобретает плоскую форму
(1-2).

В адиабатических скачках сжатия энтропия увеличивается, в скачках разряжения – уменьшается. Но в замкнутой системе энтропия убывать не может, следовательно, адиабатические скачки разряжения невозможны.

Ударные волны.Под влиянием резкого смещения поршня в трубе возникает и распространяется слева направо волна сжатия (рис.1.11).

Рис.1.11.

Пусть за бесконечно малый промежуток времени фронт волны переместится на dx. Это значит, что в области 1-Н за время dt произойдет повышение давления от Р_н до Р_1, поэтому в области 1-Н должно произойти повышение плотности на величину Ñr = r₁-r_н.

Распространение возмущений, создаваемых поршнем, можно рассматривать как совокупность непрерывно следующих друг за другом звуковых волн, причем каждая последующая волна перемещается по газу, возмущенному предыдущими волнами. Но в рассматриваемом адиабатическом и изэнтропическом движении сжатие сопровождается его подогреванием, а скорость распространения возмущений возрастает с температурой. Отсюда следует, что каждая последующая волна перемещается быстрее предыдущей. Волны догоняют друг друга, складываются и образуют одну мощную волну сжатия, называемую “ударной волной”.

Это может произойти только в случае, если некоторое количество газа, равное 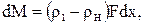перетечет из объема 1-2 в объем Н-1. Следовательно, при распространение сильной волны сжатия газ за фронтом волны находится в движении, следуя в направлении волны. По уравнению неразрывности определим скорость газового потока:

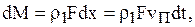
откуда 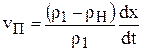. (1.54)

Но 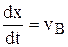, (1.55)

где v_в – скорость движения волны.

Отсюда получим равенство, связывающее скорость распространения волны (V_в) со скоростью газа, движущегося за фронтом волны в том же направлении:

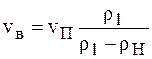. (1.56)

Применяя в области Н-1 уравнение количества движения, можно получить другое соотношение между теми же величинами.

За время dt масса газа, заполнявшая объем Н-1, перейдет из состояния покоя в движение со скоростью v_п.. Соответствующее изменение количества движения должно быть равно импульсу силы, вызванной разностью движений, действующих в сечениях 1 и Н:

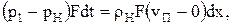
отсюда скорость волны равна

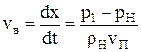. (1.57)

Подставив (1.56) в выражение (1.57), получим

. (1.58)

В случае слабой волны, когда повышение давления является незначительным, имеем:

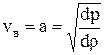. (1.59)

Слабая волна является акустической волной, распространяющейся со скоростью звука.

Из сравнения (1.58) и (1.59) видно, что скорость распространения сильной волны сжатия всегда выше скорости звука.

Распространение дозвуковой волны не сопровождается изменением состояния газа, поэтому энтропию можно считать постоянной, т.е. имеет место идеальный адиабатический процесс, в этом случае

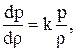
или на основании уравнения состояния для идеального газа

.

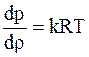Отсюда получаем известную формулу

.

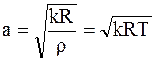Подставив (5) в (3) , получим скорость газового потока за фронтом волны сжатия:

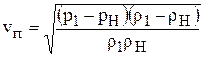. (1.60)

Свойство волны распространяться со скоростью звука приводит к тому, что при движении тела в газе с постоянной сверхзвуковой скоростью перед ним образуется ударная волна постоянной интенсивности, которая движется со скоростью движения тела.

Если фронт волны составляет прямой угол с направлением распространения, то такая волна называется прямой ударной волной (рис.1.12).

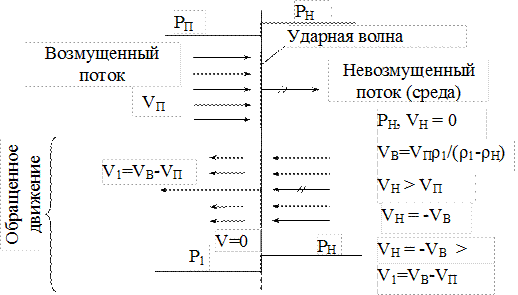
Рис.1.12.

Обычно используют правило обращенного движения, т.е. считают, что фронт волны неподвижен, а поток движется навстречу телу со скоростью, равной скорости распространения волны:

V_H = –V_В ,

т.е. сообщим мысленно всей трубе вместе с движущимся газом поступательное движение со скоростью V_В.

Тогда V₁= V_H – V_В – относительная скорость газа за фронтом волны (рис.1.13),

V_H – невозмущенный газ (набегает на волну),

V_В – скорость волны,

V_П – скорость возмущенного потока.

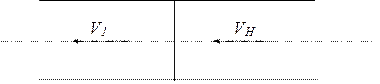
Рис.1.13.

Получилась неподвижная поверхность, при пересечении которой все струйки газа скачкообразно изменяют скорость, плотность, давление и температуру. Поэтому ударную волну называют скачком уплотнения.

Найдем связь между скоростью газа до и после скачка, площадь поперечного сечения струйки примем равной единице. Уравнение неразрывности дает:

r₁V₁ = r_нV_н . (1.61)

Пренебрегая силой трения, из уравнения количества движения получим:

р₁ – p_н = r_н V_н (V_н – V₁).

Сопоставляя эти уравнения, найдем:

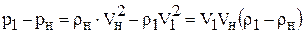. (1.62)

Откуда

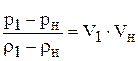. (1.63)

Если извне тепло не подводится, то теплосодержание газа постоянно. Теплоотдачей пренебрегаем.

Поэтому из уравнения теплосодержания следует:

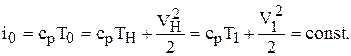
Здесь Т₀ – температура торможения.

Из этого уравнения имеем:

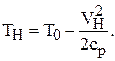
Согласно уравнению состояния газа

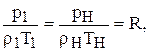
следовательно,

.

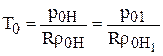Тогда, так как р_н = r_н RT_н , то

.

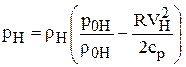Из термодинамики известно соотношение

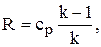
поэтому

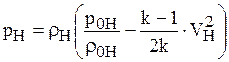. (1.64)

По аналогии получаем

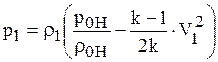. (1.65)

Вычитая равенства (1.64) из (1.65) получаем:

.

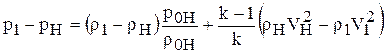Откуда на основании (1.62) выводим

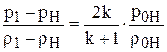. (1.66)

Используя выражение для критической скорости

,

найдем

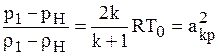. (1.67)

Сопоставляя (1.63) и (1.67), приходим к следующему простому соотношению между величинами скорости газа до и после прямого скачка

.

Это соотношение можно привести к безразмерному виду, вводя коэффициенты скорости (l = V/а_кр):

,

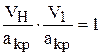или l_н ∙l₁ = 1.

Из (1.59) видно, что в прямом скачке уплотнения всегда сверхзвуковая скорость газа переходит в дозвуковую, т.к. если V_н > а_кр, то V₁ < а_кр. Следовательно, чем выше начальная скорость, тем сильнее получается скачок уплотнения. С уменьшением начальной скорости скачок ослабевает и исчезает совсем при .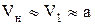

Установим далее связь между давлением и плотностью газа в скачке уплотнения. Для этого сложим равенства (1.64) и (1.65):

.

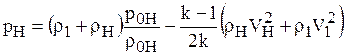Из уравнения неразрывности следует:

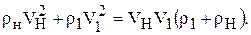
Подставим этот результат в предыдущее соотношение и получим:

откуда на основании (10) и (13) получаем основное динамическое соотношение:

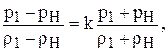(1.68)

Согласно (1.68) отношение прироста давления к приросту плотности в скачке уплотнения пропорционально отношению среднего давления к средней плотности. Отсюда следует известный уже результат, что при бесконечно малом скачке уплотнения получается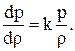

Это подтверждает предположение, что звуковой волне отвечает ударный адиабатический процесс.

Далее можно рассмотреть более детально термодинамический процесс изменения состояния газа в скачке уплотнения и найти изменение давления и плотности газа в прямом скачке уплотнения в функции числа М перед скачком.

Для этого представим предыдущее динамическое соотношение в несколько ином виде: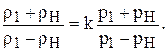

Разделив числитель и знаменатель в левой части равенства на величину r_н , а в правой р₁ , получим:

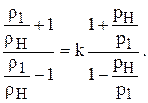
Отсюда после несложных преобразований получаем зависимость отношения r₁ /r_н от р₁ / р_н в скачке уплотнения, называющуюся ударной адиабатой:

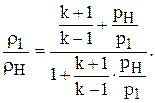(1.69)

Особенностью ударной адиабаты является то, что при неограниченном возрастании давления в скачке (P₁ ® ¥ ) уплотнения увеличение плотности имеет определенный предел, который равен

,

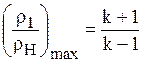в отличие от ударной адиабаты при идеальном адиабатическом процессе, в котором реализуется зависимость

.

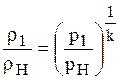Увеличение плотности с ростом давления является неограниченным (рис.1.14).

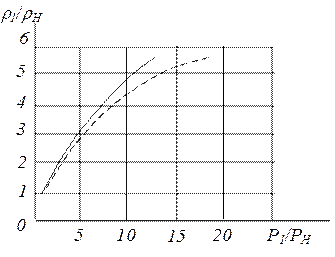
Рис.1.14.

Изменение давления и плотности в прямом скачке можно представить в функции М и l. Из уравнения количества движения с учетом формулы 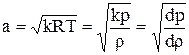и уравнения неразрывности найдем:

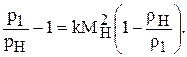
Если с помощью ударной адиабаты заменить отношение r_н / r₁ его выражением через отношение р₁ / р_н ,то после некоторых преобразований получим

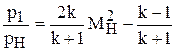. (1.70)

Учитывая, что 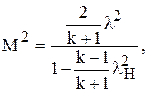это отношение можно выразить через число l:

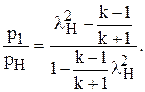(1.71)

Подставив (1.70) в (1.69), получим

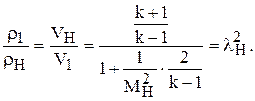(1.72)

Косые скачки уплотнения.Помимо прямых скачков уплотнения, встречаются и косые скачки уплотнения. Фронт косого скачка уплотнения располагается наклонно к направлению потока (рис.1.15).

Рис.1.15.

Косой скачок получается в случае, когда, пересекая фронт скачка, газовый поток должен изменить свое направление. Например, косой скачок получается при обтекании клиновидного тела или конуса. Поверхностью разрыва в этом случае будет конус с вершиной в носике обтекаемого тела (рис.1.16).

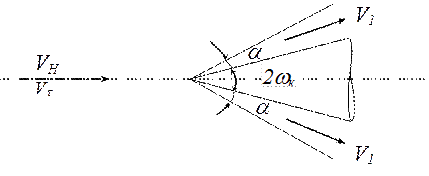
Рис.1.16. Обтекание клина

Если до встречи струи с фронтом косого скачка вектора скорости составил с ним угол a, (см. рис.1.17) то после пересечения фронта струя отклоняется на угол w, а угол между вектором скорости и фронтом скачка становится равным

b = a – w. (1.73)

Разложим вектор скорости на две компоненты, из которых одна нормальна (V_п), а другая параллельна (V_z) фронту скачка.

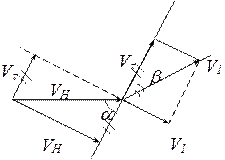
Рис.1.17.

При пересечении струй фронта косого скачка нормальная компонента скорости уменьшается

V_1n < V_Hn,, (1.74)

а тангенциальная компонента остается неизменной:

V_t = const. (1.75)

Итак, косой скачок уплотнения сводится к прямому скачку, который сносится вместе с потоком газа в сторону со скоростью V_t . В отличие от прямого, в косом претерпевает разрыв, не полная скорость газового потока, а ее компоненты, нормальные к фронту скачка.

По этой причине, по аналогии с прямым скачком, запишем, например, вместо равенства (1.63)

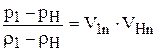(1.76)

Соответственно вместо (1.67)

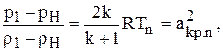(1.77)

где Т_п – температура частичного торможения.

,

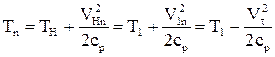а_кр.п – условная критическая скорость, соответствующая температуре частичного торможения Т_п .

Тогда

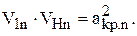(1.78)

По (1.77) свяжем полную критическую скорость с условной критической скоростью:

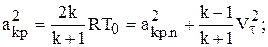(1.79)

В частном случае, когда косой скачок переходит в прямой, из соотношений (1.78) получим соотношение (1.67).

В случае косого скачка, переходя к коэффициентам скорости, будем иметь

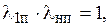где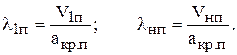

По аналогии с прямым скачком, можно получить

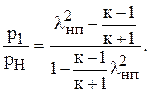
Интенсивность косого скачка уплотнения изменяется с изменением угла наклона его фронта к направлению набегающего потока. В предельном случае, когда косой скачок переходит в прямой, увеличение давления получается максимальным. В другом предельном случае, когда угол наклона скачка к направлению потока перед ним определяется условием 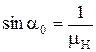, косой скачок вырождается в бесконечно слабую волну.

При симметричном сверхзвуковом обтекании конуса перед ним устанавливается коническая ударная волна, причем вершина конуса и ударной волны практически совпадают. Так как толщина скачка очень мала, приведенные формулы для косого скачка применимы к осесимметричному.

Вообще говоря, в осесимметричном случае течение отличается от плоского: скорость потока, статическое давление и плотность близки, но не равны, а углы поворота потока в скачке и на бесконечности, существенно различны. На рис. 1.18 приведены кривые значения числа М₁ за скачком и М₂ на поверхности конуса в функции угла скачка при различных значениях скорости.

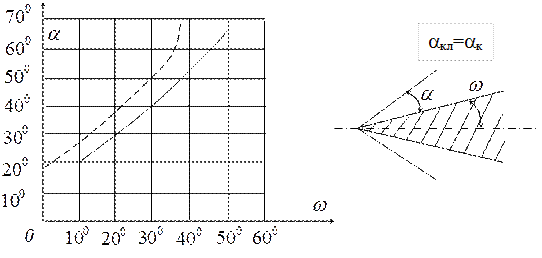
Рис.1.18.

Для практических расчетов скорость за коническим скачком можно применять равной средней арифметической величине

.

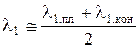Глава 2