ПОД БОЛЬШИМИ УГЛАМИ АТАКИ

Рассмотрим течения около острых конусов (10¸20^о) под углами атаки до 20¸30^о для оценки математической модели невязкого газа и возможности описания характера течения на подветренной стороне.

Между обтеканием острого конуса и плоского профиля можно провести аналогию. При нулевом угле атаки обтекание конуса осесимметрично, причем поперечное течение отсутствует. Наличие угла атаки вызывает поперечное течение. Между данным поперечным течением и течением около плоского профиля можно провести аналогию. Увеличение угла атаки равносильно повышению скорости набегающего потока на плоский профиль. При малых углах атаки поперечное течение дозвуковое. С повышением скорости набегающего потока на выпуклой поверхности профиля образуется зона со сверхзвуковым течением, которая ограничена либо звуковыми линиями, либо при определенных условиях замыкается ударной волной. Аналогично при обтекании конуса с увеличением угла атаки образуется зона сверхзвукового поперечного течения, которая при дальнейшем увеличении угла атаки замыкается ударной волной.

При обтекании цилиндра возможен отрыв потока и образование вихрей, которые либо образуют замкнутую зону в кормовой части, либо отрываются и тем самым определяют нестационарный характер течения. В случае обтекания конуса поперечный отрыв приводит к образованию незамкнутых зон стационарных вихрей. При дальнейшем увеличении угла атаки возможна асимметрия течения с образованием нестационарной вихревой дорожки.

Здесь под большими углами атаки подразумеваются углы атаки, при которых поперечное течение становится околозвуковым, что обусловливает появление внутренних ударных волн. Явления поперечного отрыва и внутренней поперечной ударной волны тесно связаны. Для круговых конусов угол атаки, при котором возможно образование поперечного отрыва на подветренной стороне, приблизительно равен углу полураствора конуса [34]. Будем считать, что если a > a_к, то угол атаки большой.

Моделирование течения при больших углах атаки имеет свои особенности, которые должны учитываться при практическом решении задач. Во-первых, требуется применять сетки с достаточно большим количеством узлов по нормальной координате. Это связано с тем, что отход головной ударной волны на подветренной стороне значительно превосходит отход ударной волны на наветренной стороне. Во-вторых, течение на подветренной стороне характеризуется тем, что головная ударная волна здесь более слабая, и при достаточно больших углах атаки она может вырождаться в характеристику.

Далее приведены некоторые результаты расчетов невязкого обтекания конусов под большими углами атаки: течение с образованием поперечной внутренней ударной волны и вихревой структуры, образование которой возможно при расчете на основе уравнений Эйлера.

На рис.2.11 приведены изолинии плотности (слева) и поперечные линии тока (справа) около конуса М=3.; g=1.4; a_к=10^о, a=20^о. Для расчета использована равномерная сетка (61´51) с выделением головной волны. Там же приведено распределение давления по поверхности конуса в зависимости от окружной координаты (тонкой линией приведено решение, полученное на неравномерной сетке). Данное распределение давления по поверхности конуса является типичным при расчете на основе уравнений Эйлера. Давление от наветренной стороны к подветренной падает до некоторой точки. Точка минимального давления соответствует месту с максимальным поперечным числом Маха (больше 1.), далее зона поперечного сверхзвукового течения замыкается поперечной ударной волной, а давление скачком возрастает до некоторого уровня, который приблизительно одинаков на всей остальной части конуса.

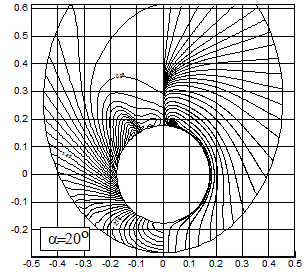
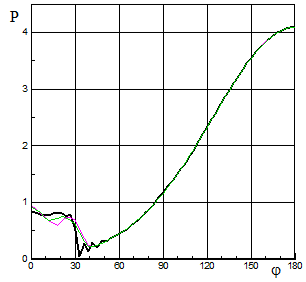
Рис.2.11

Поперечная ударная волна локально перпендикулярна поверхности тела. Это следует из факта: за ударной волной не происходит отрыв потока от поверхности тела, касательная составляющая скорости не терпит разрыва (соотношения Ренкина - Гюгонио). За поперечной ударной волной, интенсивность которой резко падает при её удалении от конуса, возможно образование вихревых структур (рис.2.11).

Давление перед поперечной ударной волной на порядок меньше единицы, что при сеточном описании функций и без выделения данной волны приводит к осцилляциям, в частности давления, которые по величине сравнимы с самим значением. Должны быть предусмотрены меры для предупреждения данных явлений: увеличение количества узлов и сглаживание. Применение сглаживания при моделировании течений около тел под большими углами атаки является вынужденным.

На рис.2.12 приведено изменения параметра установления при решении задачи на равномерной сетке (e»0.002 – решение приведено на рис.2.11) и на неравномерной сетке (e»0.0005, сетка с экспоненциальным сгущением - А=15). На неравномерной сетке решение не устанавливается.

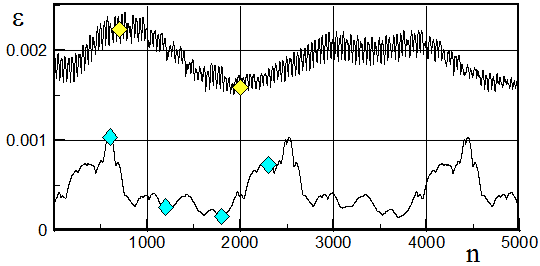
Рис.2.12

На рис.2.13 показана динамика изменения картины течения (1800 шагов) при расчете на неравномерной сетке – картины течения соответствуют моментам, отмеченными маркерами на рис.2.12. Картина течения представлена линиями тока поперечного течения. Видно периодическое (период »2000 шагов) изменение структуры течения, связанное с образованием дополнительных вихревых структур.

На рис.2.14 приведена структура течения, получаемая на равномерной сетке в два момента (также отмечены маркерами на рис.2.12). В этом случае структура течения не изменяется – решение устанавливается, а относительно увеличенное значение e связано с плохим разрешением сетки при описании поперечной ударной волны.

Образование вихревой структуры около гладких тел при расчете на основе уравнений Эйлера и определенных параметрах задачи на соответствующей расчетной сетке и схемной вязкости отмечалось в [35]. На равномерной сетке схемная вязкость позволяет выбрать решение. При уменьшении шага сетки, а следовательно и схемной вязкости, получается либо качественно новое решение, либо нестационарное решение, как в данном случае.

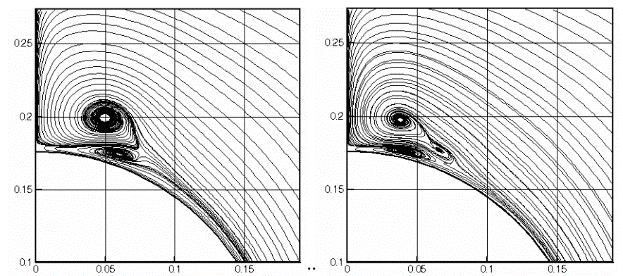
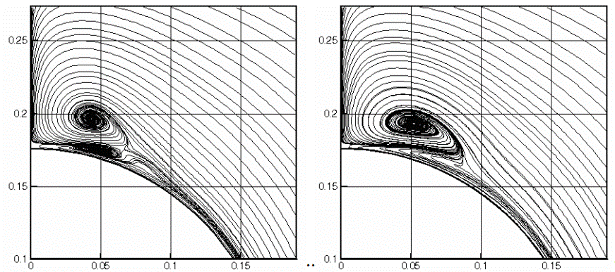
Рис.2.13

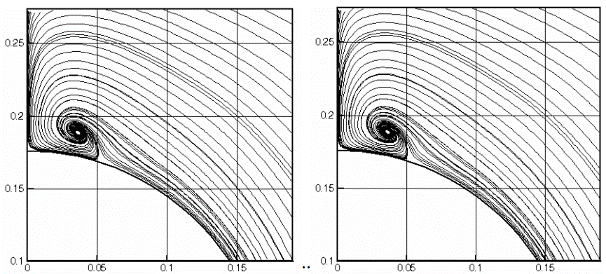
Рис.2.14

По всей видимости, исследование получаемых решений на подветренной стороне около гладких тел на основе уравнений Эйлера является в большей степени математической проблемой, но не позволяет получить физически реализуемую картину течения без специальных гипотез.