МЕТОД РАСЧЕТА КОНИЧЕСКИХ ТЕЧЕНИЙ

Рассмотрим метод расчета трехмерного невязкого конического течения. Система уравнений в этом случае имеет вид

,

, , , .

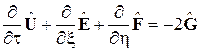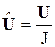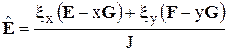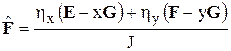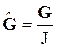Для интегрирования системы уравнений, записанной в дивергентной форме, применен метод МакКормака, основанный на использовании явной конечно-разностной схемы второго порядка аппроксимации.

Заменим область непрерывного изменения аргумента областью дискретного изменения, т.е. введем сетку:

,

, , , , .

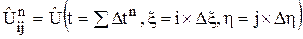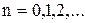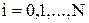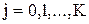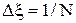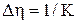Заменим дифференциальную задачу разностным аналогом. Интегрирование системы уравнений газовой динамики проводится по следующему алгоритму:

«предиктор»: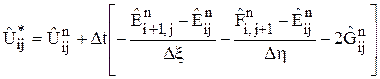

«корректор»: ,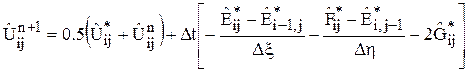

где

,

,

,

,

,

.

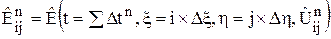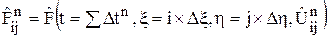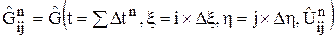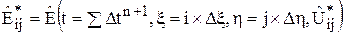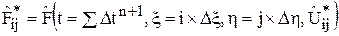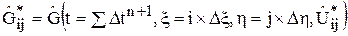Отметим использование правых разностей на шаге «предиктор» и левых на шаге «корректор». Порядок использования правых и левых разностей может быть изменен и должен выбираться в зависимости от поставленной задачи, а при расчете в граничных узлах на обоих шагах используются либо левые, либо правые разности.

Определим границы расчетной области и граничные условия на них. Будем рассматривать обтекание конического тела без угла скольжения. В качестве границ расчетной области выберем поверхности тела и ударной волны и плоскость симметрии течения. На границе расчетной области должны быть выбраны узлы расчетной сетки. Это должно делаться с учетом желания адекватного описания геометрии тела конечным числом узлов расчетной сетки, размещаемых на поверхности тела, и необходимости сгущения узлов в областях сильного изменения газодинамических функций.

На плоскости симметрии 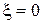, 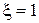должны выполняться условия симметрии: .

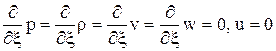Для удовлетворения данных условий вводится 4 дополнительных луча.

В случае расчета невязкого течения на поверхности тела должно выполняться условие непротекания. Процедура выполнения данного условия заключается в изменении вектора скорости после перехода на следующий временной шаг: 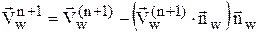. Здесь 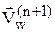- значение вектора скорости потока на теле после выполнения шага «корректор», 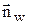- единичная нормаль к поверхности тела.

Наиболее сложной процедурой является удовлетворение граничным условиям на ударной волне. Положение ударной волны заранее неизвестно. Здесь надо отметить следующее: положение ударной волны в процессе решения изменяется, следовательно, обобщенные координаты зависят от времени, что при выводе полученной системы уравнений не учитывалось. Обобщение системы уравнений на данный случай может быть сделано, что приведет к их усложнению. В случае, когда ищется стационарное решение, представляется возможным избежать данного усложнения.

При заданном распределении узлов на ударной волне мы можем найти нормаль в каждой i-й точке поверхности ударной волны по следующим разностным формулам:

, , ,

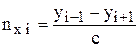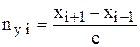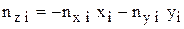где c находится из условия нормировки, индекс «i» далее опускается.

Процедура удовлетворения граничных условий на ударной волне выполнена согласно [31, 32]. Принимая за исходную величину давление за ударной волной 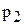, мы можем найти скорость движения ударной волны. Из соотношений Ренкина - Гюгонио имеем

.

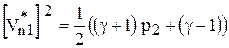Так как 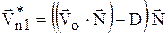, получаем .

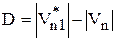Здесь 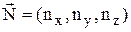- вектор единичной нормали к поверхности ударной волны, 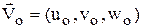- вектор скорости в набегающем потоке, D - скорость перемещения ударной волны, .

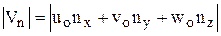Для того чтобы сетка имела достаточно упорядоченный характер, необходимо чтобы узлы, размещенные на ударной волне, могли двигаться только вдоль лучей из начала координат (x=0, y=0). По этой причине скорость ударной волны проецируется на вектор-радиус

.

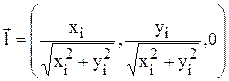Таким образом, проекция вектора скорости ударной волны на вектор-радиус есть: .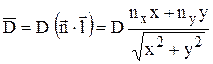

Положение ударной волны через время 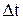может быть найдено по формулам

, .

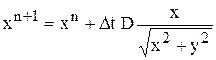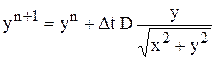Граничные условия на ударной волне удовлетворяются в два этапа. Перед выполнением шага «предиктор» в соответствии с распределением давления находится «предварительное» положение ударной волны через время 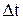- (x^*, y^*). По распределению давления за ударной волной после шага «предиктор» может быть уточнена скорость ударной волны, а, следовательно, и положение ударной волны на момент 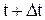. Имеем следующие формулы:

, .

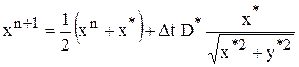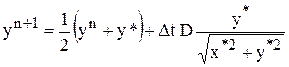После выполнения шагов «предиктор» и «корректор» на ударной волне должны быть поправлены значения плотности и скорости. Из соотношений Ренкина - Гюгонио .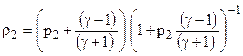

Для вектора скорости имеем следующие формулы:

, , .

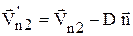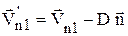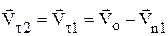Следовательно, ,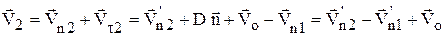

и так как 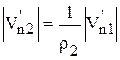, то .

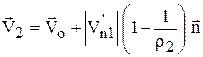При использовании явных разностных схем на размер шага по времени накладывается ограничение из условия устойчивости расчета. Воспользуемся методом локальной линеаризации. Система уравнений записывается в ви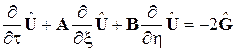де

, где , .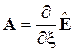

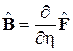Собственные значения матриц А и В:

,

,

.

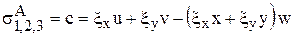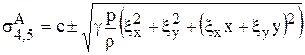
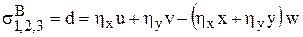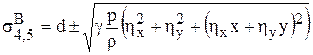Ограничение на временной шаг представляется в виде

, ,

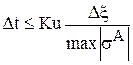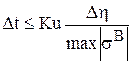где Ku - число Куранта. Обычно в расчетах полагается Ku=0.5(0.9).

Таким образом, описание численного метода решения уравнений Эйлера с соответствующими граничными условиями закончено.

ТЕСТОВЫЕ РАСЧЕТЫ

Анализ метода и проверка реализованного алгоритма в виде программы делается при расчете контрольных задач. В качестве контрольных данных используются результаты [20].

В качестве примера на рис.2.2 представлен результат расчета течения около кругового конуса со следующими значениями параметров задачи: число Маха М=3., 5.; показатель адиабаты g=1.4; угол полураствора конуса a_к=35^о, угол атаки a=10^о. Расчет обтекания конуса сделан на равномерной сетке 61´51 узлов. Сравнение проводилось по распределению газодинамических величин в возмущенной области течения. За исключением распределения плотности на поверхности конуса имеется хорошее соответствие между данными [20] и выполненным расчетом. На рис.2.2 представлено распределение плотности и давления на поверхности тела (маркерами – известные данные, тонкими линиями – расчет). Распределение давления практически совпадают. В распределении плотности наибольшее различие имеем на подветренной стороне (j=0^о). Отметим, что уже в следующем слое по нормали полученные значения плотности и давления совпадают с данными [20].

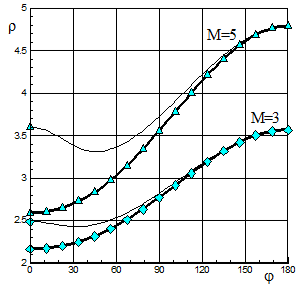
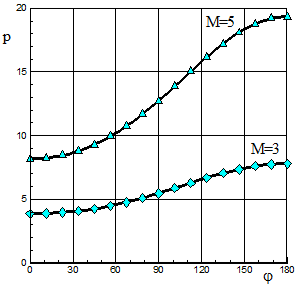
Рис.2.2

В [20] приводятся два значения параметров течения на поверхности тела с подветренной стороны. Значения получаются предельными переходами: a) h®0, j=0 - по нормали к поверхности тела; б) h=0, j®0 - вдоль поверхности тела от наветренной стороны к подветренной. Значение, полученное переходом а), совпадает с рассчитанным здесь значением.

Различие в распределении плотности на поверхности тела объясняется тем, что (в отличие от [20]) не предполагалась постоянная величина энтропии на всей поверхности тела. Для полного соответствия с результатами [20] нужно модифицировать систему удовлетворения граничных условий на поверхности конуса. Это реализуется алгоритмом, предложенном в [31, 32]. После выполнения шага «корректор» вектор скорости 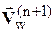не удовлетворяет условию непротекания и должен быть повернут от касательной плоскости к поверхности тела на некоторый угол d. Угол определяется выражением 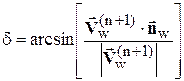. Если d>0, то при повороте вектора скорости происходит расширение потока, если d<0 - сжатие. Изменение давления в потоке при повороте вектора скорости на бесконечно малый угол d дается следующим выражением [31]:

,

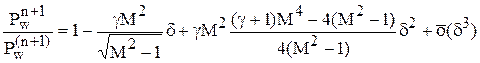где 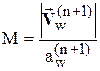, 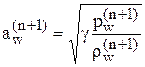. Далее, в предположении сохранения энтропии вдоль поверхности тела, находится новое значение плотности 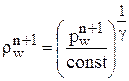, где const определяется согласно давлению и плотности в критической точке на наветренной стороне конуса.

Величина вектора скорости находится из интеграла Бернулли:

.

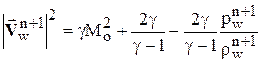Так как вектор 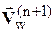был повернут в плоскости векторов 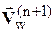, 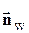на угол d, то направление скорости 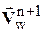теперь должно совпадать с направлением 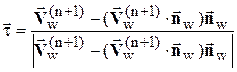, то есть .

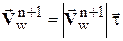Удовлетворение граничных условий по данному алгоритму обеспечивает, помимо выполнения условия непротекания, также сохранение энтропии на поверхности конуса.

Расчет с удовлетворением граничных условий на поверхности тела по описанной выше схеме позволяет получить решение, которое находится в соответствии с [20]. На рис.2.2 приведено жирными линиями полученное решение с выполнением условия постоянства энтропии на поверхности тела. В этом случае наблюдается полное соответствие с данными [20]. Отметим, что на распределение давления на поверхности тела данное условие не оказывает влияния, и, следовательно, интегральные аэродинамические характеристики - подъемная сила и волновое сопротивление - не зависят от требования постоянства энтропии на поверхности тела.

При аэродинамическом проектировании в основном представляют интерес суммарные (или интегральные) аэродинамические характеристики: подъемная сила и положение центра давления. Коэффициент нормальной подъемной силы определяется в виде интеграла соответствующей величины вдоль поверхности тела: 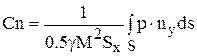, здесь Cn - коэффициент нормальной силы, n_y - проекция вектора нормали на координатную ось Y, ds - элемент поверхности тела, M - число Маха, S_х - характерная площадь. При рассмотрении обтекания конуса за характерную площадь обычно принимается площадь основания конуса.

Центр давления конуса при предположении, что течение коническое, расположен на 2/3 длины конуса от вершины.

На рис.2.3 приведено сравнение полученных и расчетных значений согласно [20] коэффициентов Cn и Cx при угле атаки a=5^o в зависимости от угла полураствора конуса a_к при числе Маха М=5 и на рис.2.4 - в зависимости от М при a_к=15^о.

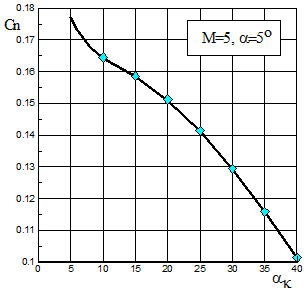
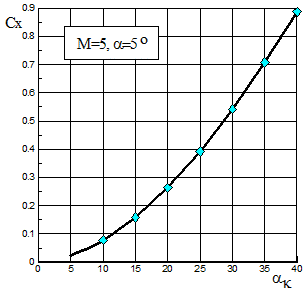
Рис.2.3

На рис.2.5 приведено сравнение расчетных (линия) и экспериментальных [43, 44] (маркеры) значений коэффициента Cn при М=4 в зависимости от угла атаки для варианта конуса с углом полураствора a_к=5^о. Там же приведены изолинии давления (слева) с шагом 0.1 и поперечные линии тока (справа) при углах атаки a=5, 10, 20^о. В данном случае представляет интерес возможность расчета нелинейного характера изменения Cn в зависимости от a для конусов с малым углом полураствора конуса. Есть соответствие расчета и эксперимента не только при малых, но и при достаточно больших a - в области нелинейного изменения подъемной силы. Соответствие расчетных данных экспериментальным в интегральных характеристиках есть следствие того, что основной вклад в подъемную силу создает распределение давления на наветренной части, а распределение давления на подветренной части оказывает малое влияние.

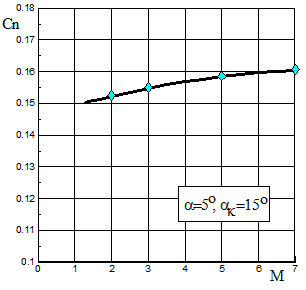
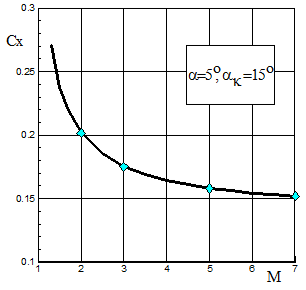
Рис.2.4

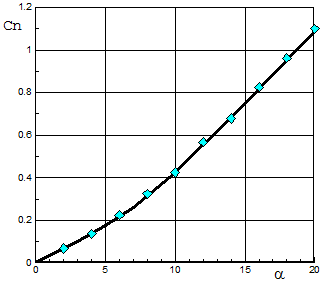
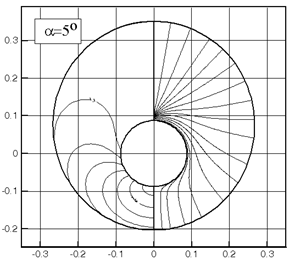
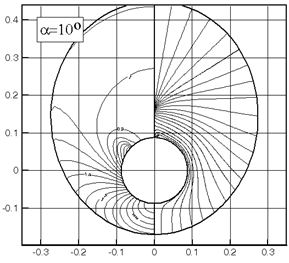
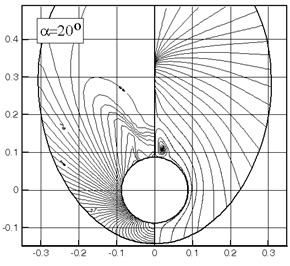
Рис.2.5

На рис.2.6 приведены положения головной ударной волны (тангенс угла наклона поверхности волны относительно оси конуса) и изобары около конуса: М=7.; g=1.4; a_к=30^о, a=5, 10, 15, 20^о. Данное течение представляет интерес по той причине, что максимальный отход головной ударной волны реализуется не в плоскости симметрии течения. Маркерами отмечено положение ударной волны согласно данным [20]. Есть соответствие расчетов.

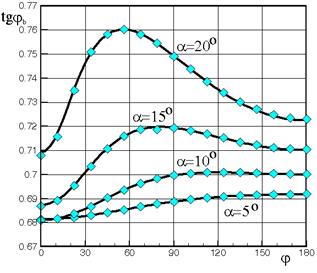
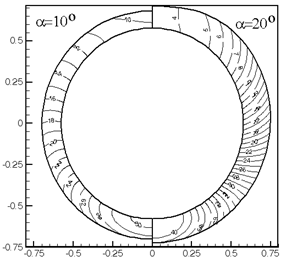
Рис.2.6

Остановимся на понятии «установление решения». В качестве параметра установления используется максимальное значение разности давления во всех узлах расчетной сетки между шагами по времени 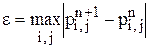. Практически за конечное число шагов нельзя получить решение, которое бы не изменяло значение искомых газодинамических величин в узлах сетки. Считается, что установление имеет место, если за определенное количество итераций по временной координате значение функции во всех узлах изменяются на величину, не большую чем определенная малая величина 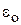(причем в качестве функции контроля установления может использоваться не только давление, но и другие газодинамические функции). Данное условие "установления" имеет четкую математическую формулировку. Для каждого класса задач величина 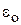определяется экспериментально после проведения тестовых расчетов.

Главный критерий установления - неизменность картины течения при установлении. Анализ картины течения осуществляется с помощью представления информации в графическом виде; количественного наблюдения за поведением решения в некоторых характерных точках; сравнения расчетов, полученных на разных сетках и при различных способах постановки начальных и граничных условий; характерного времени установления; исследования поведения решения при изменении параметров задачи.

По результатам тестовых расчетов было получено, что величина 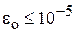обеспечивает соответствие конечных решений при решении с одинаковыми параметрами независимо от начальных данных.

На рис.2.7 приведено распределение процессорного времени вычислительной машины при использовании алгебраической сетки. Количество необходимых шагов по времени до установления зависит от размера сетки, изменяется в пределах от одной до нескольких десятков тысяч.

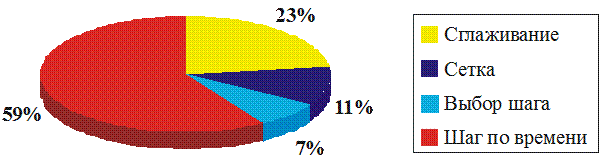
Рис.2.7

Программа реализована на языке FORTRAN и состоит из основной программы и ряда подпрограмм. На рис.2.8 приведена блок-схема программы расчета с выделением головной волны.

Составные части:

1. Задание начальных газодинамических полей и расчетной сетки. Начальное поле течения может формироваться различными способами: условия в набегающем потоке; результат расчета осесимметричной задачи; результат расчета течения с достаточно близкими значениями параметров задачи из базы ранее проведенных расчетов.

2. Вычисление метрических коэффициентов.В принципе метрические коэффициенты вычисляются по координатам узлов расчетной сетки. При ограничении на память постоянно возможно иметь в памяти информацию только о координатах узлов сетки, А при каждой необходимости производить требуемые вычисления. Однако это приводит к существенным затратам процессорного времени. Целесообразно выделение памяти под метрические коэффициенты. Если расчет осуществляется без выделения головной ударной волны на фиксированной сетке, то процедура вычисления метрических коэффициентов выполняется один раз, а её результат постоянно хранится в памяти. Если расчет осуществляется с выделением головной ударной волны, то процедура вычисления метрических коэффициентов выполняется каждый раз при изменении расчетной сетки.

3. Выбор (вычисление) шага интегрирования по времени. Шаг выбирается из условия устойчивости.

4. Удовлетворение граничных условий на внешней границе. Расчет скорости движения внешней границы и её положения, изменение расчетной сетки в соответствии с изменением положения внешней границы. Данные процедуры связаны с удовлетворением граничных условий на головной ударной волне. Если делается расчет без выделения головной ударной волны, то расчетная сетка фиксирована, и в этом случае выполнение данных процедур не требуется.

5. Вычисление консервативных величин E, F, G. Вычисление U (шаги «предиктор» и «корректор»).

6. Удовлетворение граничных условий на поверхности тела, в плоскости симметрии.

7. Сглаживание. Понятие сглаживания и необходимость его применения будут рассмотрены ниже.

Рис.2.8