РАСЧЕТ БЕЗ ВЫДЕЛЕНИЯ ГОЛОВНОЙ УДАРНОЙ ВОЛНЫ

Рассмотрим возможность расчета обтекания без выделения головной ударной волны. В этом случае строится фиксированная расчетная сетка, при этом значительно упрощается схема удовлетворения граничных условий на внешней границе (на ней просто поддерживаются условия в набегающем потоке) и можно применить локальный шаг интегрирования. На рис.2.8 выделены жирным шрифтом части программы, которые остаются необходимыми при расчете с фиксированной сеткой (без выделения головной волны). Объем вычислений на шаг интегрирования уменьшается более чем на 10 % (рис.2.7), не надо перестраивать сетку.

Остановимся на понятии «локальный шаг интегрирования». В случае получения решения методом установления (а не исследования нестационарного процесса) важно получить конечный результат, поэтому можно допустить локальный шаг интегрирования, то есть в каждой точке пространства интегрировать уравнения по времени со своим локальным шагом по времени, который определяется местными условиями и местным распределением узлов расчетной сетки.

При написании условия устойчивости предполагается, что выбирается минимальный шаг по времени во всем пространстве. Фактически для всех узлов расчетной сетки используется один шаг по времени. В любой задаче, если рассчитать значение шага интегрирования, то оно изменяется в широком диапазоне для различных узлов сетки. В частности, использование сеток со сгущением около поверхности тела приводит к тому, что шаг интегрирования по времени резко уменьшается - шаг интегрирования определяется в области наибольшего сгущения. Число Куранта для большинства расчетных узлов значительно меньше единицы. Это существенно увеличивает число итераций, необходимых для установления. Наиболее очевидный путь сокращения числа итераций в рамках явной схемы заключается в том, чтобы время в каждом узле расчетной сетки шло независимо, т.е. в каждом узле шаг интегрирования выбирается только в соответствии с местными условиями.

Использование локального шага интегрирования в условиях изменения расчетной сетки (при выделении головной волны) обычно приводит к неустойчивому счету (разрушение решения), что, по всей видимости, связано с мгновенной передачей возмущений от внешней границы на всю область посредством смещения узлов, и в условиях независимости времени в каждом узле приводит к рассогласованию решения.

При использовании фиксированной сетки экспериментально получено, что локальный шаг интегрирования можно применять при числе Куранта Ku=0.5. На равномерных сетках при расчете с локальным шагом интегрирования потребное количество шагов до установления уменьшается незначительно, что связано с тем, что шаг интегрирования на такой сетке в зависимости от пространства изменяется несущественно.

При переходе от равномерных к неравномерным сеткам преимущества локального шага интегрирования существенно возрастают. На рис.2.9 приведена сходимость решения при общем и локальном шаге интегрирования задачи об обтекании конуса с параметрами: М=3.; g=1.4; a_к=35^о, a=10^о.

Сетка сгущается экспоненциально по нормали к поверхности конуса по закону 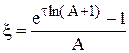, здесь t - равномерно распределена на [0;1]; A - константа, степень сгущения увеличивается по мере увеличения A. Величина А=15 обеспечивает уменьшение размера сетки около поверхности конуса в 5 раз. Сходимость показана для двух вариантов неравномерной сетки при А=15 и А=45. Значение А=45 обеспечивает уменьшение минимального размера расчетной сетки еще в 2 раза. В качестве начальных условий используется решение, полученное на равномерной сетке.

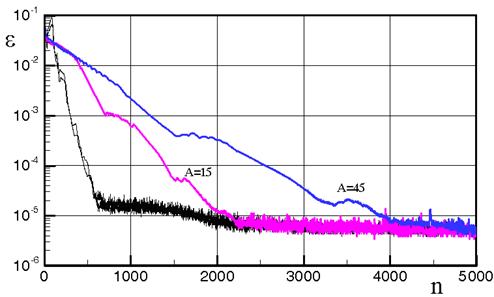
Рис.2.9

При использовании локального шага интегрирования количество итераций до установления одинаково для обеих сеток (сходимость при использовании локального шага интегрирования на рисунке приведена тонкими линиями), при использовании одинакового для всех узлов шага - увеличивается в 2 раза (при А=15). В данном случае количество итераций увеличивается пропорционально сгущению узлов, так как шаг интегрирования определяется именно размером расчетной сетки по нормали. Локальный шаг интегрирования позволяет распространяться возмущениям со скоростью 1 узел за шаг при числе Куранта Ku=1 независимо от сгущения сетки.

Возможность расчета без выделения ударных волн обеспечивается использованием системы уравнений в консервативном виде. Консервативный вид уравнений при переходе к разностной задаче обеспечивает выполнение законов сохранения в интегральном виде.

Расчет без выделения ударных волн имеет свой недостаток, связанный с тем, что при сеточном описании функций ударные волны «размазываются». Это приводит к тому, что при расчетах без выделения ударных волн требуются достаточно мелкие сетки, которые должны позволять локализовать положение ударной волн с учетом ее «размазывания», а также вводить процедуру сглаживания решения.

На рис.2.10 приведены результаты расчета обтекания конуса: М=3.; g=1.4; a_к=10^о, a=10^о – изолинии давления с выделением (слева) и без выделения головной волны (справа). Для подавления осцилляций используется сглаживание [33]: ,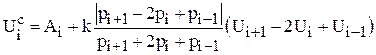

где p - давление, U_i - компоненты вектора U, k=0.1 ¸ 0.5.

Сглаживание необходимо применять не только при расчетах без выделения головной ударной волны. В ряде случаев: плохие начальные данные (резкое изменение условий обтекания или геометрии тела), исследование течений с большими градиентами - расчет неустойчив без сглаживания. Это объясняется тем, что возмущения в процессе перестройки решения передаются в виде достаточно сильных ударных волн, которые также необходимо сглаживать.

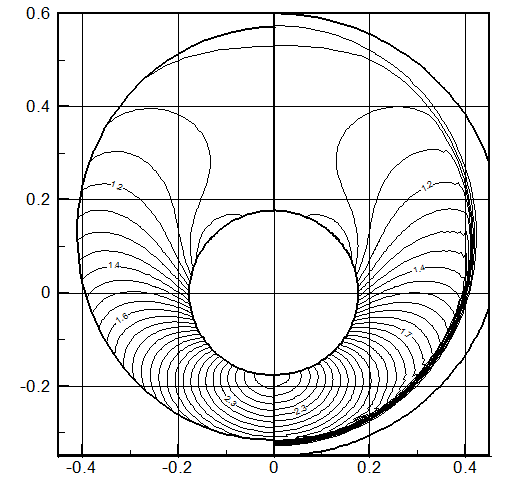
Рис.2.10

Отказ от выделения головной ударной волны дает дополнительные преимущества при использовании конвейерного или многопроцессорного вычислителя. При решении уравнений математической физики большое значение имеют граничные условия. Необходим достаточно сложный алгоритм их удовлетворения, который в большинстве случаев не имеет смысла выполнять в виде векторных операций по причине недостаточно большой размерности, сложных алгебраических выражений. Именно по этой причине (и если это возможно) должны ставиться наиболее простые граничные условия, даже если это требует увеличения числа расчетных узлов. В этом случае почти весь объем вычислений выполняется на достаточно длинных массивах, а выполнение обычных операций (невекторных) сокращается. Применение методов сквозного счета при использовании конвейерного процессора более целесообразно. Отметим также, что в данной работе применены простые алгебраические методы построения сетки. При исследовании течений в геометрически сложных областях затраты на построение сетки могут значительно возрасти.