Закон сохранения количества движения и уравнение движения. Уравнения для скорости (сохранения количества движения) выведем сначала для идеальной жидкости (без вязкости).
Закон сохранения импульса для движущегося малого объема W жидкой частицы (с непроницаемыми стенками) есть
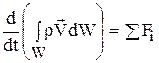 , (1.14)
, (1.14)
где в правой части стоит сумма всех сил, действующих на выделенный объем, причем для простоты будем вначале предполагать, что внутренний приток массы отсутствует (M'=0). Ограничиваясь рассмотрением массовой силы Fm (например, центробежной или силы тяжести, действующих на единицу массы, [н/кг]) и сил давления P (действующих на единицу площади, [н/м2]), запишем
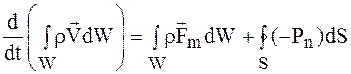 .
.
Учитывая, что 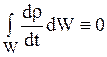 (интеграл берется по жидкой частице, то есть по заданному количеству жидкости), и, преобразуя поверхностный интеграл давления в объемный, можно переписать уравнение в виде
(интеграл берется по жидкой частице, то есть по заданному количеству жидкости), и, преобразуя поверхностный интеграл давления в объемный, можно переписать уравнение в виде
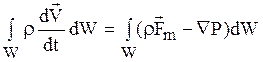 . (1.15)
. (1.15)
Это закон сохранения количества движения в интегральной форме.
Исходя из произвольного выбора объема жидкой частицы, можно перейти к дифференциальной форме:
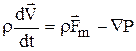 . (1.16)
. (1.16)
Это закон сохранения количества движения в форме Лагранжа.
Входящая в уравнение производная dV/dt – это субстанциональная производная, которая описывает изменение скорости жидкой частицы.
Используя связь субстанциональной (полной) производной по времени с частной производной скорости по времени (изменение скорости в заданной точке), полученную ранее, приходим к другой дифференциальной форме уравнения сохранения количества движения (форме Эйлера):
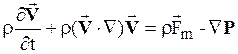 . (1.17)
. (1.17)
Это уравнение Эйлера, оно получено им еще в 1755 г. Данное уравнение выражает закон сохранения количества движения (импульса).
В проекциях на оси декартовой системы это уравнение имеет вид
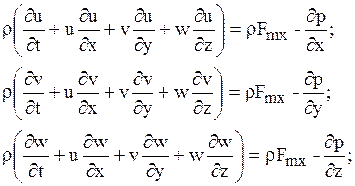
Запишем полученные уравнения движения в другой форме – в форме переноса импульса. Для этого выполним следующие преобразования, используя уравнение неразрывности:
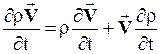 , но
, но 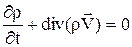 ,
,
тогда 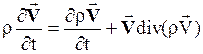 и, следовательно,
и, следовательно,
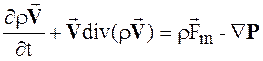 . (1.18)
. (1.18)
В декартовой системе координат эти уравнения имеют вид
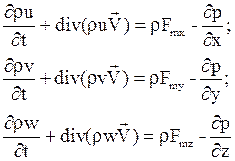
или
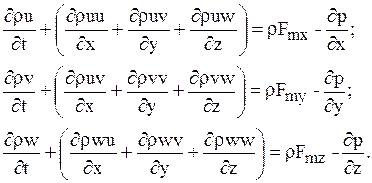
Эти уравнения, как и в случае уравнения неразрывности, могут быть получены еще одним способом. Выделим в потоке движущейся массы фиксированный элементарный параллелепипед со сторонами dx, dy, dz и подсчитаем массу жидкости, протекающей через него за время dt.
Выделим в потоке газа или жидкости элементарный параллелепипед с ребрами dx, dy, dz. На выделенный объем действуют массовые силы (например, инерционные, гравитационные), поверхностные силы – давления и трения. Найдем проекции этих сил на ось х (рис.1.5):
а) массовые силы приложим в центре элемента объемом dw.
Ее проекция на ось х равна:
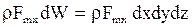 ,
,
аналогично на другие оси;
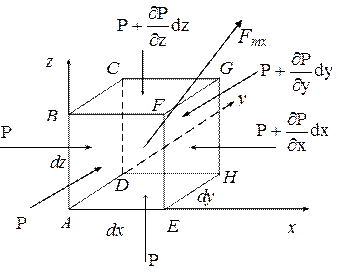
Рис.1.5
б) сила давления. На левой грани элемента по оси x удельное давление равно Р, на площадку dydz действует сила Pdydz. На противоположной грани удельное давление равно 
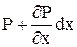 , а на эту грань действует сила
, а на эту грань действует сила 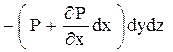 . Знак «–» указывает на то, что сила действует против направления оси х. Равнодействующая этих сил равна их алгебраической сумме:
. Знак «–» указывает на то, что сила действует против направления оси х. Равнодействующая этих сил равна их алгебраической сумме:
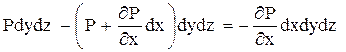 .
.
Суммируя силы, получим проекцию на ось х равнодействующих всех сил, приложенных к объему dW:
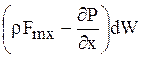 . (1.19)
. (1.19)
Согласно второму закону механики равнодействующая равна произведению массы элемента ρdW на его ускорение dVx /dt:
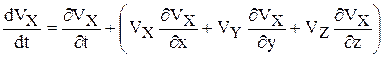 ,
,
где 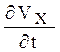 - локальное,
- локальное, 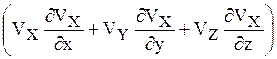 - конвективное изменение величины Vх , d/dt – субстанциальная производная:
- конвективное изменение величины Vх , d/dt – субстанциальная производная:
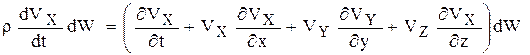 . (1.20)
. (1.20)
Приравнивая уравнения (1.19) и (1.20), получим:
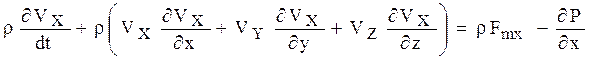 .
.
Аналогично запишем уравнения для проекций сил на оси y и z:
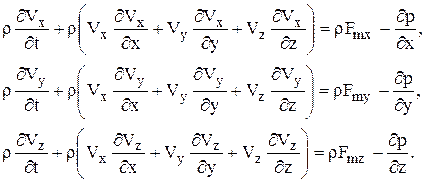
Это уравнение движения. Его часто записывают в виде
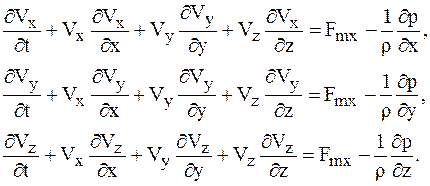
В случае стационарности процесса первые члены уравнения будут равны нулю.
Рассмотрим теперь данный закон для реальной жидкости, учитывая вязкость (внутреннее трение). Начнем с рассмотрения уравнений движения для изотермической жидкости и еще раз напомним, что уравнение непрерывности справедливо и для реальной жидкости, так как его вывод основывался только на законе сохранения вещества. Воспользуемся уравнением, записанным в форме закона для переноса импульса идеальной жидкости, и допишем в него слагаемые, отвечающие за перенос импульса в результате действия вязких сил.
Главный вектор количества движения К системы материальных частиц равен интегралу от произведений их элементарных масс dm на векторы скоростей частиц V:
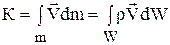 .
.
Применим к объему W массой m теорему об изменении главного вектора количества движения. Приравняв полную производную по времени от главного вектора количеств движения главному вектору внешних массовых F и поверхностных P сил, получим
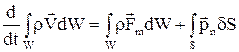 , (13)
, (13)
где pn – результирующая составляющая внутренних сил в газе (сил давления и напряжений вязкости), приложенная к поверхности S объема W.
Вычислим полную производную от главного вектора, причем для простоты будем вначале предполагать, что внутренний приток массы отсутствует (M'=0), тогда
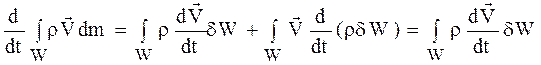 . (1.22)
. (1.22)
Чтобы преобразовать поверхностный интеграл в правой части (13) в объемный, перепишем его в виде:
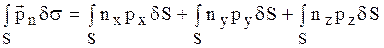 ,
,
где pх , py , pz – вектор напряжений, приложенный к положительным сторонам площадки, и применим формулы векторного анализа:
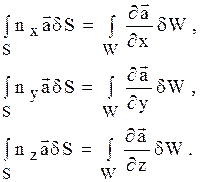 (1.23)
(1.23)
Тогда будем иметь
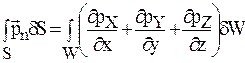 . (1.24)
. (1.24)
Подставляя в (1.16) значения входящих в него величин и перенеся все члены в одну строку, получим
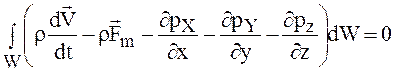 . (1.25)
. (1.25)
Используя положение о произвольности объема W и приравнивая подынтегральную функцию нулю, получим
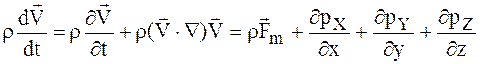 . (1.26)
. (1.26)
Проектируя обе части равенства на направления осей координат, получим:
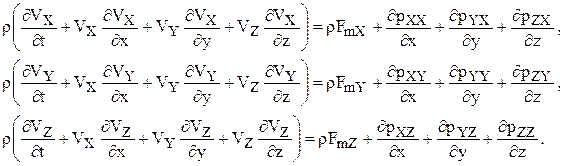 (1.27)
(1.27)
Эти уравнения динамики сплошной среды «в напряжениях», или «уравнения импульсов».
Cила трения на единицу поверхности по закону Ньютона
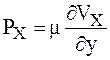 (μ – коэффициент динамической вязкости, Н×с/м2).
(μ – коэффициент динамической вязкости, Н×с/м2).
Подставив это выражение в предыдущее уравнение и принимая μ = const, получим
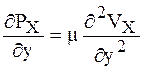 .
.
В общем случае, когда Vx изменяется по трем направлениям, проекция силы трения на ось х определяется выражением
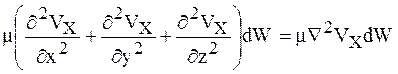 .
.
Суммируя силы, получим проекцию на ось х равнодействующих всех сил, приложенных к объему dW:
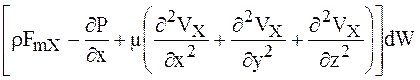 . (1.28)
. (1.28)
Получим уравнения движения с учетом вязкости, используя подход, изображенный на рис.1.5. Добавим силу трения, определив ее из рассмотрения плоского ламинарного потока, в котором скорость Vx изменяется лишь в направлении оси y. В этом случае сила трения s возникает лишь на боковых гранях элемента (рис.1.6).
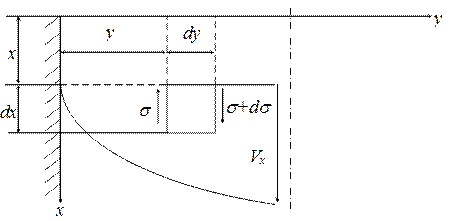
Рис.1.6.
Около левой грани скорости движения частиц меньше, чем в самом элементе, поэтому здесь в сечении 'y' сила трения направлена против движения и равна – sdxdz. У правой грани скорость движения больше, чем в самом элементе, поэтому здесь в сечении 'y+dy' сила трения направлена в сторону движения и равна
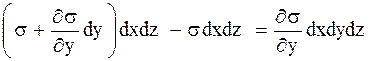 .
.
Здесь 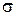 – сила трения на единицу поверхности, по закону Ньютона.
– сила трения на единицу поверхности, по закону Ньютона.
Подставив это выражение в предыдущее уравнение и принимая μ = const, получим 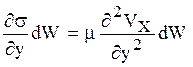 .
.
В общем случае, когда Vx изменяется по трем направлениям, проекция силы трения на ось х определяется выражением
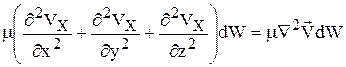 .
.
Суммируя силы, получим проекцию на ось х равнодействующих всех сил, приложенных к объему dW:
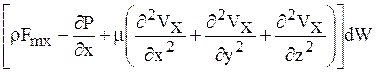 . (1.29)
. (1.29)
Используя вновь понятие субстанциальной производной
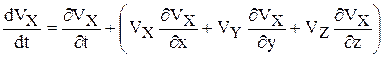 ,
,
согласно второму закону механики получим:
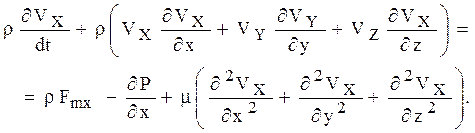
Аналогично запишем уравнения для проекций сил на оси y и z (учитывая, что 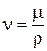 ):
):
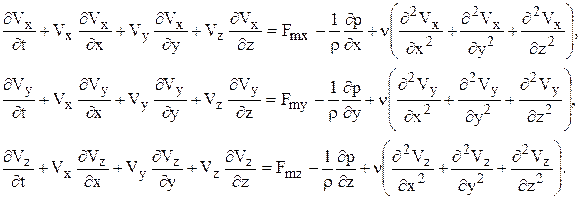
Эти уравнения движения называют уравнениями Навье-Стокса. Дифференциальное уравнение движения в форме Навье-Стокса описывает движение вязкой сжимаемой жидкости или газа и справедливо как для ламинарного, так и для турбулентного движения.
В случае гипотезы “идеального газа” уравнения движения Навье - Стокса переходят в уравнения Эйлера:
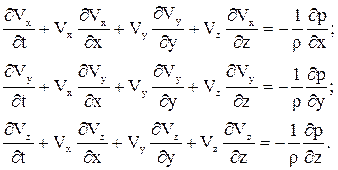 (1.30)
(1.30)
В случае стационарности процесса первые члены уравнения будут равны нулю. Для двух- и одномерного движения уравнения Навье-Стокса и Эйлера соответствующим образом упрощаются.
Закон сохранения энергии. Закон сохранения энергии не только устанавливает неизменность всей энергии для любой выделенной массы жидкости или газа, но и отражает взаимопреобразование различных форм движения материи, и в первую очередь механической энергии в тепловую. Для расчета этих преобразований служит уравнение баланса энергии, выводимое из общего термодинамического закона сохранения энергии, который для индивидуального (непроницаемого) объема движущейся среды формулируется так:
– изменение полной энергии выделенного объема жидкости или газа за единицу времени равно сумме работ приложенных к нему массовых и поверхностных внешних сил на поверхностях, ограничивающих этот объем, и подведенного извне тепла за то же время.
Этот закон выражается интегральным равенством
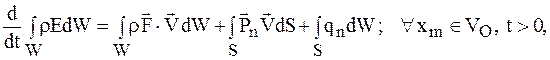 (1.31)
(1.31)
где 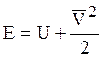 – удельная полная энергия; U = cvT – удельная внутренняя энергия;
– удельная полная энергия; U = cvT – удельная внутренняя энергия; 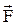 – результирующая массовых сил,
– результирующая массовых сил, 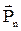 – результирующая составляющая внутренних сил в газе (сил давления и напряжений вязкости), приложенная к поверхности S выделенного объема W; q – удельное количество энергии (обычно тепла), подводимое в единицу времени к рабочему телу в выделенном объеме.
– результирующая составляющая внутренних сил в газе (сил давления и напряжений вязкости), приложенная к поверхности S выделенного объема W; q – удельное количество энергии (обычно тепла), подводимое в единицу времени к рабочему телу в выделенном объеме.
Учитывая произвольность выделенного объема W, получаем дифференциальную форму данного закона:
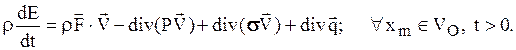 (1.32)
(1.32)
Необходимость введения уравнения энергии следует из того, что два уравнения – неразрывности (скалярное) и движения (векторное) – содержат три неизвестных величины: одну векторную (скорость 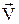 ) и две скалярные (давление р и плотность r), поэтому для газа (W=var) число искомых величин на одну больше, чем число уравнений. Если присоединить уравнение энергии, то добавится ещё одна неизвестная величина – температура Т. Система уравнений получиться замкнутой присоединением уравнения состояния, и тогда задача аэрогазодинамики (при заданных граничных и начальных условиях) становится определенной.
) и две скалярные (давление р и плотность r), поэтому для газа (W=var) число искомых величин на одну больше, чем число уравнений. Если присоединить уравнение энергии, то добавится ещё одна неизвестная величина – температура Т. Система уравнений получиться замкнутой присоединением уравнения состояния, и тогда задача аэрогазодинамики (при заданных граничных и начальных условиях) становится определенной.
Если рассматривается идеальная несжимаемая жидкость, то полагают, что в жидкости отсутствуют теплообмен и трение. В таком случае движение адиабатично в каждой жидкой частице. Следовательно, закон сохранения энергии выливается в утверждение, что энергия каждого жидкого элемента остается постоянной:
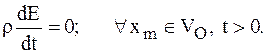
Отсюда следует, что для описания движения идеальной несжимаемой жидкости уравнение энергии не используется.
Дата добавления: 2016-09-06; просмотров: 8495;











