СИСТЕМА УРАВНЕНИЙ АЭРОГАЗОДИНАМИКИ

Анализ системы уравнений аэрогазодинамики с точки зрения различных технических задач. Система уравнений газодинамического процесса в общем виде имеет вид:

- уравнение неразрывности

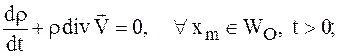(1.33)

- уравнение количества движения

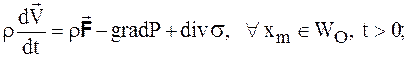(1.34)

- уравнение энергии

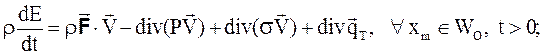(1.35)

– уравнение состояния:

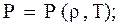(1.36)

В дивергентной форме:

– для идеального газа

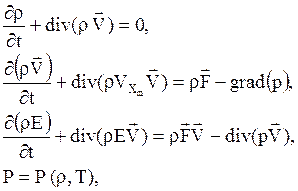
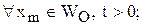
– для вязкого теплопроводного газа

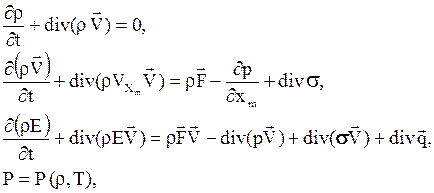
где W_O - объем области; t – время, 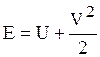- удельная полная энергия, 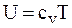- удельная внутренняя энергия, 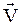- вектор скорости потока в данной точке; P и Т - местные термодинамическое давление и температура; x_m - пространственные координаты; r - плот­ность среды; 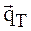= –l grad(T) – вектор плотности теплового потока; l – коэффициент теплопроводности, c_v – удельная теплоемкость; s – тензор напряжений, вызванных силами вязкости

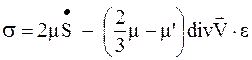, (1.37)

где 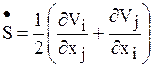- тензор скоростей деформаций, V_i - проекции вектора скорости на оси координат x_i; e – единичный тензор, m - коэффициент внутреннего трения (динамический коэффициент молекулярной вязкости) движущейся среды, m' - коэффициент объемной вязкости (во многих случаях им можно пренебрегать).

Здесь первое уравнение – массопереноса, второе уравнение – движения, третье – энергии и последнее –состояния.

Систему уравнений аэрогазодинамики идеального газа в дивергентной форме в проекциях на оси декартовой системы координат имеет вид:

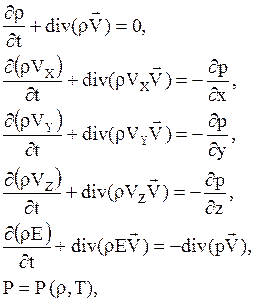
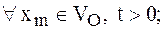
или в развернутом виде:

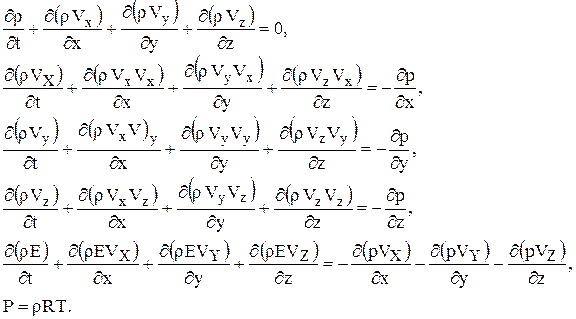
В осесимметричном двумерном случае, характерном для многих задач в области ракетостроения, данная система уравнений принимает следующий вид:

уравнение неразрывности

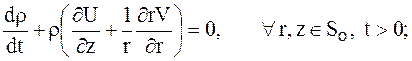
уравнения импульса

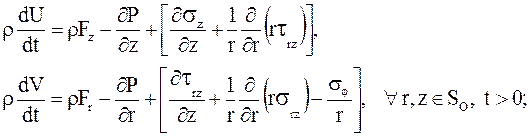
уравнение энергии

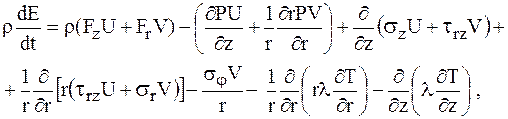
где U, V – составляющие скорости по осям z и r соответственно; формулы для напряжений вязкости имеют вид:

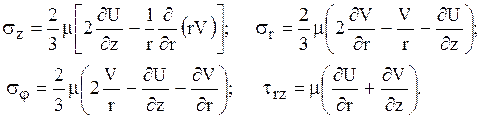
Решение представленных систем в общем случае затруднительно, поэтому при решении конкретных технических задач вводят ряд допущений. Проанализируем наиболее часто встречающиеся:

1 - мерность течения. В конкретных приложениях бывает возможным рассматривать процесс массообмена в термодинамической (“нульмерной”) нестационарной постановке (p, r, T=f(t)); одномерной стационарной (p, r, T, V=f(x)); одномерной нестационарной (p, r, T, V=f(x,t)); двумерной стационарной (p, r, T, V=f(x,y)); двумерной нестационарной (p, r, T, V=f(x,y,t)); трехмерной стационарной или нестационарной.

2 - в ряде случаев возможно пренебречь вязкостью (m=0). При этом уравнение Навье-Стокса переходят в уравнение Эйлера и задача существенно упрощается;

3 - сжимаемость (r=var). Свойство сжимаемости рабочего тела характеризуется модулем объемной упругости Е, определяемой по зависимости

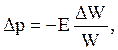(1.38)

где 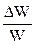- относительное изменение объема, вызванное изменением давления на величину Dp.

Сжимаемость воздуха при атмосферном давлении и температуре 0⁰С в 20 000 раз больше сжимаемости воды. Аналогичное соотношение имеет место и для других газов. Учитывая, что равенство (1.38) на основе закона сохранения массы можно записать в виде

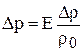, (1.39)

течение рабочего тела можно рассматривать как несжимаемое, пока относительное изменение плотности остается малым, т.е.

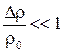(1.40)

или пока динамическое давление остается весьма малым по сравнению с модулем объемной упругости

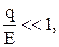(1.41)

где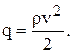

Введя в рассмотрение скорость звука “с”, которая определяется по формуле Лапласа

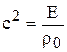(местная скорость звука)

используя (1.39) получаем

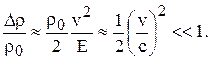
Следовательно, течение можно рассматривать несжимаемым, если

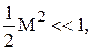
где M - число Маха.

Для воздуха это возможно до скорости V = 0.3 C, при этом

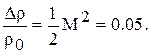
Массовые силы.В большинстве прикладных задач, когда поток рассматривается однофазным, массовыми силами пренебрегают. Исключение составляют процессы газодинамики во вращающихся объектах.

Адиабатность, изэнтропность, баротропность процесса.Приняв, что движущийся газ является идеальным и изолированным от внешнего теплообмена, процесс становится адиабатным. Энтропия S во всех точках потока при этом постоянна и уравнение (1.40) переходит в адиабату Пуассона:

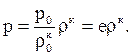(1.42)

Движение в этом случае является баротропным, т.е. давление является только функцией скорости потока р = f (v) и определяется адиабатой (1.42). В этом случае, если давление p = f (r,T), т.е. температура в газе меняется, процесс называется бароклинным.

Краевые условия или условия однозначности. Краевые условия или условия однозначности включают в себя:

- геометрические условия, характеризующие форму и размеры системы, в которой протекают процессы;

- физические, характеризующие физические свойства среды и тела;

- граничные условия, характеризующие протекание процесса на границах тела;

- временные условия, характеризующие особенности протекания процесса во времени.

Краевые условия позволяют выделить из бесконечного множества решений единственное.

При установившемся движении начальные условия выпадают, при неустановившемся они представляют собой значение в начальный момент времени скорости, давления, температуры и т.д. в каждой точке.

Граничные условия могут быть заданы на свободной поверхности или на твердых границах. Если невязкая жидкость или газ соприкасается с непроницаемой поверхностью, уравнение которой F(x,y,z) = 0, то граничное условие состоит в том, что по всей поверхности скорость касательна к ней (“условие безотрывного обтекания”): (V_n)_s = 0.

Так как градиент функции F(x,y,z) совпадает с нормалью к поверхности уровня, то

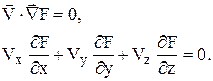
Если граница меняется со временем и уравнение поверхности имеет вид F(x,y,z,t)=0, то граничным условием будет совпадение координат частицы с координатами поверхности x, y, z в момент времени t и в момент времени t+dt , когда координаты будут x+dx, y+dy, z+dz. т.е. для этого момента времени координаты частицы должны удовлетворять уравнению

F(x+dx,y+dy,z+dz,t+dt)=0.

Ограничиваясь первыми членами разложения в ряд Тейлора, получим

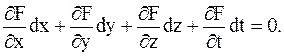
Разделив на dt, получим граничное условие в следующей форме:

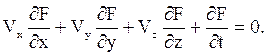
В случае обтекания тела вязким потоком задают, как правило, равенство скорости на стенке нулю, т.е. “условие прилипания”:

(V)_s = 0.

Примером задания граничного условия на свободной поверхности является равенство давления на ней внешнему давлению:

P(x ,y, z, t) = P₀.

Граничными условиями при изучении обтекания тел с теплообменом могут быть, например, распределение температуры на поверхности тела или поток тепла в каждой точке поверхности, или температура обтекающей тело среды и закон теплообмена между ними.