Вычисление теплового потока. Энтропия

Как следует из первого закона термодинамики, внутренняя энергия системы, т.е. энергия ее внутримолекулярного и межмолекулярного движения накапливается и расходуется за счет двух принципиально различных потоков энергии - работы и теплообмена. Причем, в количественном отношении обе формы потока энергии могут даже компенсировать друг друга. Так, возможен процесс, когда теплоприток, поступающий к системе, совпадает по величине с работой системы, направленной во внешнюю среду: Q = L. В таком процессе согласно первому закону внутренняя энергия системы будет оставаться неизменной, U₂=U₁, но неизменной только в количественном отношении. Изменения, конечно, неизбежны, но уже в отношении качества внутренней энергии. А именно, может и должен изменяться характер внутримолекулярного и межмолекулярного движения как носителя внутренней энергии. Что понимается под изменением качества внутренней энергии, следует из теоретической физики. Там выясняется, что наблюдаемое равновесное состояние термодинамической системы (ее макросостояние) на самом деле есть непрерывная хаотичная последовательность огромного множества отличающихся друг от друга микросостояний – мгновенной совокупности значений энергии каждой из множества частиц. Эти микросостояния (кадры) непрерывно чередуются в пределах данного макросостояния вследствие переноса энергии между движущимися частицами при их столкновениях, вообще при их взаимодействиях. В силу принципа квантования энергии численность микросостояний (отличающихся кадров) выражается хотя и очень большим, но конечным числом. Это число микросостояний напрямую не связано ни одним из выше рассмотренных параметров и функций равновесного состояния системы. Следовательно, оно само является самостоятельным параметром или функцией равновесного состояния термодинамической системы, определяя качество ее внутренней энергии. При совершении равновесной работы (адиабатный процесс) число микросостояний не меняется, при теплообмене – меняется. Для отображения этого числа в термодинамике предусмотрена специальная величина - удельная энтропия. Ее обозначение - s, единица измерения - кДж/кг/К. Соответственно

S = s.m , кДж/ К

- энтропия системы массой m.

В таблицах термодинамических свойств рабочих тел удельная энтропия s представлена наряду с энтальпией как функция каких-либо двух термических параметров состояния, обычно температуры и давления.

В курсах физики и в классических руководствах по термодинамике приводится несколько способов доказательства, что удельный тепловой поток dq в случае равновесного процесса связан с изменением удельной энтропии ds системы равенством

dq = T ds, (1-6)

где Т – абсолютная термодинамическая температура, выраженная в кельвинах, s – удельная энтропия, кДж/кг/К.

Видно, что энтропия не меняется (ds=0) в равновесном адиабатном процессе, при dq=0.

Отсюда уравнение первого закона для одного кг закрытой системы принимает вид

T ds = du + p dv. (1-7)

Его называют основным уравнением термодинамики для равновесных процессов. Эти уравнения открывают дорогу к вычислениям в случаях, когда в закрытой системе задан равновесный процесс, например, изотермический, изобарный или др., и известны термодинамические свойства рабочего тела в каждом состоянии, через которое проходит процесс.

Равенство (1-6) позволяет универсальным способом вычислять тепловые потоки в любых равновесных процессах, лишь бы была известна зависимость между температурой и энтропией процесса. Действительно, для произвольного равновесного процесса из состояния 1 в состояние 2 удельный теплоприток определится формулой общего вида

q = 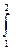T ds.

В частном случае равновесного изотермического процесса (Т = const) имеем

q = T (s₂ - s₁ ). (1-8)