ОСНОВНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ
И РАВНОВЕСИЯ СПЛОШНОЙ СРЕДЫ
Распределение массы в сплошной среде. Закон сохранения массы и уравнение неразрывности. Возьмем малый объем жидкости или газа DW, содержащий внутри себя данную точку М пространства, и пусть масса этого объема будет Dm; скалярная величина r, определяемая предельным выражением
r=lim(Dm/DW), при DW ® 0, (1.5)
называется плотностью распределения массы или, короче, плотностью среды в данной точке М. Причем предполагается, что при стремлении объема DW к нулю точка М все время остается внутри объема. Обратную величину v = 1/r называют удельным объемом.
Переходя к бесконечно малым величинам, получим
dm=rdW.
Плотность движущейся среды зависит от ее материального состава, от температуры и давления, а также и от характера движения среды. В общем случае плотность представляется функцией пространственных координат и времени
r= r (х, у, z, t)
и образует скалярное поле, которое может быть как стационарным, так и нестационарным.
Поверхности или, в частном случае плоского распределения, линии уровня скалярного поля плотностей называют изостерическими поверхностями или линиями (изостерами).
Плотность как масса, отнесенная к единице объема, измеряется в кг/м3.
Выделим в пространстве некоторый малый (неподвижный, недеформируемый) объем W, через который движется жидкость (подход Эйлера). Объем ограничен поверхностью S, а его масса в данный момент времени t равна
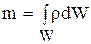 .
.
Применим к этому объему закон сохранения массы сплошной среды, справедливый для классической нерелятивистской механики. Масса газа в выделенном в пространстве объеме может изменяться лишь за счет внутренних источников массы M' и за счет перетекания жидкости через поверхность, ограничивающую объем. Вытекающий из объема через поверхность S поток жидкости определяется формулой
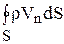 ,
,
где n – внешняя нормаль к поверхности.
Если за положительное направление нормали n принять направление движения из рассматриваемого объема (внешняя нормаль), то условие сохранения массы этого объема во времени можно записать в виде
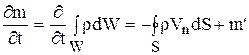 , (1.6)
, (1.6)
а при отсутствии внутренних источников массы
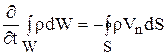 ,
,
где 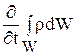 – изменение массы объема; m'=M'×W – скорость изменения массы объема W за счет внутреннего источника; M' – удельная скорость изменения массы (в 1 м3).
– изменение массы объема; m'=M'×W – скорость изменения массы объема W за счет внутреннего источника; M' – удельная скорость изменения массы (в 1 м3).
Первое слагаемое в правой части преобразуем по теореме Остроградского-Гаусса:
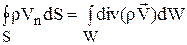 .
.
Тогда при отсутствии внутренних источников
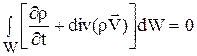 , (1.7)
, (1.7)
а так как равенство должно быть справедливо для любого объема, то подынтегральное выражение должно удовлетворять уравнению
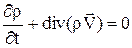 , (1.8)
, (1.8)
которое называют уравнением неразрывности (непрерывности) в форме Эйлера.
Для несжимаемой жидкости плотность есть величина постоянная (r=const ), и уравнение (1.8) упрощается:
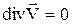 . (1.9)
. (1.9)
Важно отметить, что уравнение неразрывности справедливо и для идеальной, и для реальной жидкостей.
Если внутри объема W происходит прирост массы за счет внутренних источников массы, то в правой части уравнения сохранения необходимо добавить источник
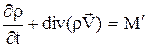 . (1.10)
. (1.10)
В декартовой прямоугольной системе координат уравнение неразрывности примет вид
 . (1.11)
. (1.11)
Для несжимаемой жидкости
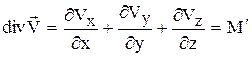 . (1.12)
. (1.12)
Учитывая, что из векторного анализа следует
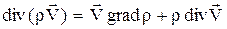 ,
,
можно записать уравнение неразрывности в виде
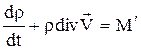 . (1.13)
. (1.13)
Рассмотрим другой подход к выводу уравнения неразрывности (в форме Лагранжа). Рассматривая малый замкнутый движущийся в пространстве изменяющийся объем (с непроницаемыми стенками), имеем для элементарной массы m газа в этом объеме w,
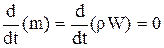 ,
,
где d/dt – символ полной производной по времени. Производя дифференцирование произведения функций (rW) и используя представление о дивергенции вектора скорости как скорости объемного расширения, получим
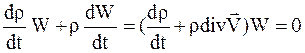 .
.
Отсюда в силу произвольности величины W следует уравнение неразрывности в форме Лагранжа
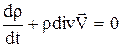 .
.
Эти уравнения могут быть получены еще одним способом. Выделим в потоке движущейся массы фиксированный в пространстве элементарный параллелепипед со сторонами dx, dy, dz и подсчитаем массу жидкости, протекающей через него за время dt (рис.1.4).
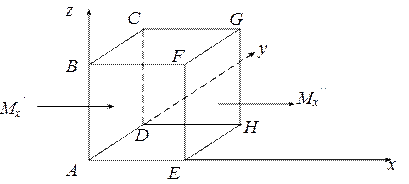
Рис.1.4
В направлении оси х через грань АВСD втекает масса газа или жидкости Mx1, равная
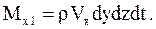
Через противоположную грань EFGH вытекает масса Mx2 :
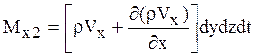 .
.
Излишек массы жидкости, вытекающей из объема в направлении оси х:
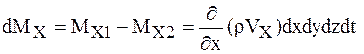 .
.
Полный избыток массы равен сумме этих выражений
 .
.
Перенося все члены в левую часть равенства, получим (8).
В случае стационарного поля плотности
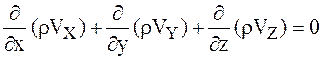 .
.
Дата добавления: 2016-09-06; просмотров: 2234;











