Методика оптимизации времени диагностирования и замены элементов с накопленной повреждаемостью
Существенным недостатком технической диагностики является высокая трудоемкость этих методов, связанная с замером контролируемых параметров посредством широкой гаммы средств технической диагностики. Особенно это относится к диагностированию одинаковых элементов в большом количестве (ролики, подшипники, зубчатые передачи). Затраты, связанные с диагностикой таких элементов, снижают общую эффективность ТО и поэтому требуется оптимизация времени проведения очередной диагностики. Методика оптимизации:
| |


Первые четыре этапа отражают процесс накопления повреждаемости и диагностики как Марковский процесс:
1 – отражает изменение распределения элементов по величине накопленной повреждаемости на каждом цикле положения і в начальный момент времени 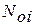 и в текущий момент времени
и в текущий момент времени 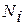 .
.
2 – реализует в момент времени 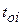 на определенной стадии диагностирования;
на определенной стадии диагностирования;
3 – предусматривает выделение 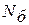 бракованных элементов, накопленная повреждаемость которых не позволяет эффективно использовать ГМ, а также формировать вектор
бракованных элементов, накопленная повреждаемость которых не позволяет эффективно использовать ГМ, а также формировать вектор 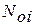 – распределение элементов, замена которых не целесообразна.
– распределение элементов, замена которых не целесообразна.
4 – предусматривает замену бракованных элементов на новые и формирование вектора распределения заменяемых элементов по накопленной повреждаемости.
В результате четырех этапов определяется вектор 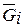 .
.
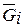 – распределение данных о закономерностях формирования накопления повреждаемости элементов. Этот вектор определяется методами математической статистики и представляет собой скорость накопления повреждаемости
– распределение данных о закономерностях формирования накопления повреждаемости элементов. Этот вектор определяется методами математической статистики и представляет собой скорость накопления повреждаемости 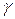 , ее среднее значение
, ее среднее значение 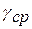 и дисперсию. Выбор закона распределения осуществляется на основе критерия Пирсона
и дисперсию. Выбор закона распределения осуществляется на основе критерия Пирсона 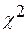 по величине сходимости результата прогнозируемой скорости накопления и по статистическим данным. На основе данных
по величине сходимости результата прогнозируемой скорости накопления и по статистическим данным. На основе данных 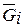 формируются матрицы вероятностей накопления повреждений. Так, при известном законе изменения скорости
формируются матрицы вероятностей накопления повреждений. Так, при известном законе изменения скорости 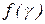 можно определить вероятность перехода элемента из класса j в класс i по условию:
можно определить вероятность перехода элемента из класса j в класс i по условию:
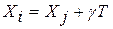 ,
,
где 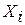 и
и 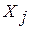 – средние для i-го и j-го классов соответственно;
– средние для i-го и j-го классов соответственно;
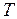 – время, в течение которого происходит накопление повреждаемости от уровня i до уровня j.
– время, в течение которого происходит накопление повреждаемости от уровня i до уровня j.
В зависимости от закона распределения можно получить различные формулы для определения матрицы переходов.
Для нормального закона матрица перехода из класса j в класс i:
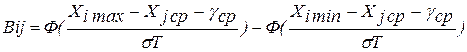 .
.
Для логнормального закона:
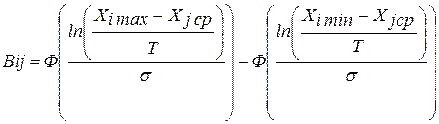 .
.
Для экспоненциального закона:
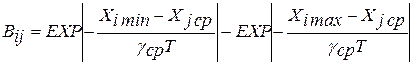 .
.
Для закона Релея:


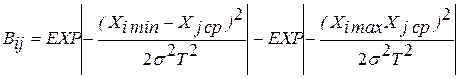 .
.
Для первого цикла закон распределения и его параметры принимаются по статистическим данным элементов аналогичных машин и в дальнейшем корректируются по результатам замены в последующих циклах.
В зависимости от функционального назначения элементов и их типов в машине потеря работоспособности может выражаться в виде снижения эксплуатационных характеристик, уменьшения запасов прочности, увеличения нагрузок в элементах ГМ. Выразив влияние накопленной повреждаемости диагностируемого элемента на l-тый показатель ее работоспособности в виде зависимости 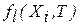 , условие обеспечения оптимального времени очередной диагностики запишется в виде:
, условие обеспечения оптимального времени очередной диагностики запишется в виде:
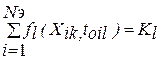 ,
,
где 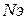 - количество групп элементов, накопленная повреждаемость которых определяет l-тый показатель работоспособности;
- количество групп элементов, накопленная повреждаемость которых определяет l-тый показатель работоспособности;
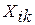 - вектор повреждаемости k-того элемента на i-том цикле;
- вектор повреждаемости k-того элемента на i-том цикле;
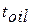 - оптимальное время очередной диагностики на i-том цикле по l-тому показателю;
- оптимальное время очередной диагностики на i-том цикле по l-тому показателю;
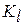 - допустимая потеря работоспособности машины по l-тому показателю (определяется по экономическим соображениям или по условию безопасности работ).
- допустимая потеря работоспособности машины по l-тому показателю (определяется по экономическим соображениям или по условию безопасности работ).
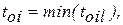
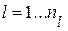 .
.
Дата добавления: 2020-12-11; просмотров: 527;











