Математическая модель процесса выбраковки и замены диагностируемых элементов с накопленной поврежденностью

Накопленная повреждаемость – накопление в элементе необратимых повреждений, которые могут носить как механический характер (изнашивание, усталость, накопление пластических деформаций), так и физико-механический характер (коррозия, эрозия, старение). Наиболее общий метод описания процесса повреждаемости разработан Болотиным и основан на введении скалярной величины повреждений ψ(t). Как правило, удобно брать нормированную ψ(t):

ψ(t) = 0 – повреждений нет;

ψ(t) = 1 – объект не может далее эксплуатироваться.

Пусть в случае разрушения элемента параметром, определяющим меру повреждаемости, будет Х, который влияет на качество функционирования машины. С течением времени Х(t) будет монотонно изменяться и в конце концов достигнет своего предельного состояния Х_пр. Отличительной особенностью этого процесса является то, что будущие замеры Х_k(t) не зависят от текущего Х_i(t) и от предшествующего Х_j(t) состояний. Такой процесс в математике называется Марковским процессом. Бесконечное число состояний может быть с достаточной точностью представлено в виде конечного числа дискретных состояний: Х₁, Х₂ ,... Х_n.

Если известна условная вероятность перехода из состояния j в состояние k:

,

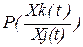а также известна вероятность нахождения элемента в состоянии j:

Р(Х_j(t)),

то для Марковского процесса вероятность нахождения в состоянии k:

Р( 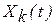)= Р(Х_j(t))*Р( ).

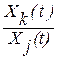Модель вложенной цепи Маркова представляет собой циклический процесс (т.е. изменение параметра Х в течение цикла происходит скачком). При этом есть возможность более точного определения параметра Х путем дробления цикла. Модель позволяет решать задачу определения времени безопасного функционирования элемента по причине изменения параметра Х, планировать периодичность осмотров и число необходимых запасных частей. Для группы N однотипных элементов математическая модель накопления повреждаемости запишется в виде:

,

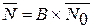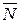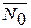где и – вектора-столбцы распределения элементов по накопленной повреждаемости в текущий и в начальный момент времени;

В – матрица вероятностей перехода элементов группы из одного класса повреждаемости в другой класс.

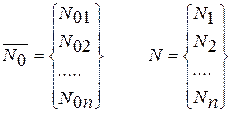
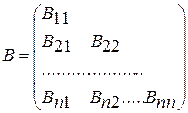
Учитывая, что процесс накопления повреждаемости носит аддитивный характер, вероятность перехода из класса с большим номером в класс с меньшим номером равна нулю, а для каждого j-того класса:

.

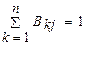Число элементов групп, накопленная повреждаемость которых превышает допустимый уровень, т.е. элементов, подлежащих выбраковке, определяется по зависимости:

.

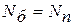Распределение элементов, оставшихся в эксплуатации по классам запишем в виде:

.

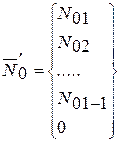После выбраковки по результатам на машину будет установлено 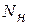новых элементов, численно равных количеству выбракованных:

,

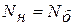тогда распределение по классам повреждаемости вновь поставленных элементов:

.

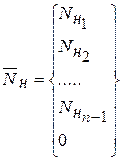Количество элементов в начале следующего цикла и распределение их по классам:

.

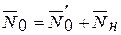Таким образом, математическое моделирование закончено.