Построение параметрической регрессионной модели

Будем аппроксимировать (приближено описывать) М_х(Y) некоторой заранее выбранной непрерывной функцией с параметрами

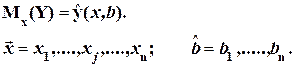(2.7)

Пусть неизвестный вектор параметров 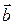находится (оценивается) каким-либо методом, например методом наименьших квадратов (МНК).

Вид функции 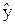(·) выбирается заранее, а еще лучше подбирается с учетом имеющихся наблюдений с использованием «Мастера диаграмм» в программной среде Excel.

Пример:

Здесь подходящей аппроксимирующей функцией является парабола:

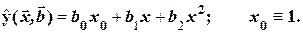(2.8)

Подставляя уравнение (2.7) в уравнение (2.5) получаем конкретное уравнение регрессии (параметрическую модель):

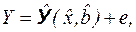(2.9)

где е – случайные ошибки аппроксимации (остатки), которые включают в себя как ошибки аппроксимации (неточного описания), так и случайные возмущения данных, в частности вызванные неучтенными в модели регрессорами.

В i – ом наблюдении

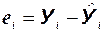
– расчетное значение по уравнению регрессии; y_i – наблюдаемое значение для свободного члена Y.

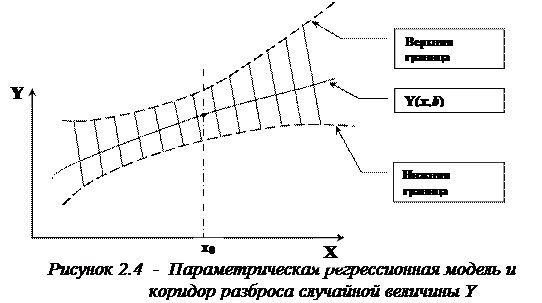
Параметрическая регрессионная модель (2.9) описывает усредненную зависимость Y от 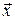в некотором коридоре своего случайного разброса. Другими словами – линия регрессии 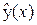– это средняя линия трубки в случае одной переменной.

В случае многих независимых переменных 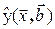описывает серединную поверхность. Ее называют «поверхность отклика» (реакции объекта на воздействие 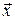): 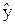– следствие; 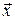– причина (воздействие на объект).