Основная предпосылка эконометрического анализа

Суть основной предпосылки построения эффективной эконометрической модели состоит в возможности разбиения Y на две части: объясненную и случайную

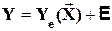. (2.1)

Объясненная часть случайной величины 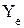, формируется вариацией вектора независимых переменных ;

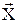E – случайная составляющая (остаток).

Если случайная величина Y непрерывна, то объясненная часть 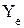представляет собой некоторую неизвестную непрерывную функцию от регрессоров :

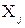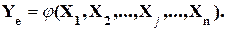(2.2)

Естественной аппроксимацией (описанием) случайной функции 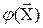является оценка:

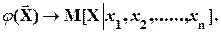(2.3)

М[Х½х₁, х₂,… х_n, ] - среднее значение случайной функции 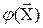, т.е. условное математическое ожидание, полученное при условии, что вектор независимых переменных принял конкретное (фиксированное) значение:

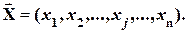
Здесь и далее большими буквами X, Y будет обозначаться текущее значение случайных величин, а малыми буквами, x, y их конкретные (количественные) реализации.

В некоторых книгах используют более компактное обозначение:

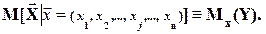(2.4)

Тогда основную предпосылку построения эконометрической модели можно записать так:

Y = М_х(Y) + E_.(2.5)

Уравнение:

Y_e = М_х(Y) = j (х₁, х₂, …,х_j,…, х_n)_.(2.6)

называется уравнением регрессии. Заметим, что вид истинной функции 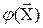в уравнении (1.6) нам пока неизвестен.

Замечание: Эконометрическая модель (2.6) не всегда является регрессионной, т.е. объясненная часть случайной величины 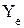не всегда равна своему условному математическому ожиданию:

Y_e ¹ М_х(Y).

Пример: Пусть независимые переменные 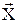измерены с систематическими ошибками. Тогда неизвестная нам случайная функция 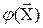в наблюдениях будет деформирована (искажена). В эконометрике это встречается часто. Существуют специальные методы борьбы с этим неприятным обстоятельством, которые будут рассмотрены ниже.

Критерием того, что модель (1.6) является регрессионной является условие М_х(E) = 0. Действительно, записав основную предпосылку эконометрического анализа (2.5),

Вычислим математическое ожидание от обеих частей уравнения:

М_х(Y) = М_х [М_х(Y)] + М_х(E);Þ

Þ М_х(E) = 0(2.6)

Условие (1.6) является наиболее существенным условием получения качественной модели. Статистически это условие означает отсутствие систематического смещения наблюдений 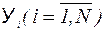, относительно линии (или поверхности в многомерном случае) регрессии.