Основные принципы расположения небесных тел в Евклидовом пространстве. Основные принципы силового взаимодействия небесных тел.

СилойFназывается мера механического взаимодействия материальных тел.

Сила - векторная величина и ее действие на тело определяется:

- модулем или численным значением силы

- направлением силы

- точкой приложения силы

Модуль силы является скаляром, из чего: Сила есть всегда положительная величина.
Не существует «отрицательной силы притяжения» или «отрицательной силы отталкивания». Есть только положительные силы. В природе, а значит и в физике, имеет место быть только:
1. Сила притяжения – всегда положительная величина, значение от нуля, до плюс бесконечности [ 0;+∞)
2. Сила отталкивания – всегда положительная величина, значение от нуля до плюс бесконечности [ 0;+∞) .

Силовые взаимодействия небесных тел в рамках Евклидового пространства регламентируются основным законом Небесной Механики - Законом Всемирного Тяготения. 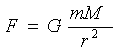,из которого следует: неограниченная пространственная продолжительность гравитационного взаимодействия, напрямую вытекающая из зависимости . Из чего: значение силы с удалением уменьшается до сколь угодно малых величин, но при этом не может быть равным нулю.

Взаимодействие и перемещение тел в реальном трехмерном пространстве регламентируется:

Третьим Законом Ньютона. Из которого следует, что перемещение отдельно взятого тела в рамках Небесной Механики приводит к взаимному(пусть незначительному но) перемещению всех без исключения небесных тел.

Согласно Третьему Закону Ньютона падение даже незначительной массы в сторону Солнца, хоть и в самом малом количественном выражении, но вызывает встречное перемещение Солнца. В равной степени это относится ко всем без исключения небесным телам.

Силовые взаимодействия небесных тел в рамках реального трёхмерного пространства также регламентируются взаимным силовым равновесием.

Согласно данного условия,вселенское взаимодействие, построенное на силах притяжения имеет строгий порядок, обусловленный взаимным орбитальным движением, позволяющий телам удерживать свое расположение в пространстве и избегать комплексного разрушения системы, вследствие закономерной для сил притяжения динамики образования макротела.

Наглядно эти принципы взаимодействия можно отследить на модели газа (близком силовом аналоге).

Как известно, молекулы газа находятся в силовом взаимодействии, в силу чего при ряде условий занимают друг относительно друга равноудаленное расположение в пространстве. Кроме силового взаимодействия, молекулы ни чем не «скованы» в своем перемещении в обозначенном пространстве и при стечении различных факторов, часть из них может выстраиваться, например, в одну линию.

Рис. .№6. Рис. .№7. Рис. .№8

Но ни при каких обстоятельствах в линию не могут выстроиться все молекулы газа. И это обусловлено не только ничтожной вероятностью такого расположения, но и обусловлено силовой невозможностью такого распределения. Поскольку силы взаимодействия между самими молекулами препятствуют такому расположению.

Если всё же

предположить, что молекулы газа, размещенные в замкнутом пространстве (резервуаре) могли бы «выстроиться в одну линию, то в таком случае отмечалась бы разница давления газа на стенки резервуара. Давление по линии распределения молекул было бы больше чем в других направлениях.Такая частная ситуация на практике невозможна. И молекулы газа всегда занимают положение соответствующее комплексному силовому равновесию.

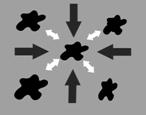
Если рассматривать теоретическую модель газа, при которой, силами взаимодействия являютсяне силы взаимного отталкивания, а силы притяжения (в чистом виде), то вполне очевидна силовая динамика, при которой взаимное притяжение молекул приводит к лавинообразному процессу образования единого скопления (все молекулы устремляются в общий центр).

При таких условиях, невозможно предполагать какого либо, равномерного распределения молекул по объему.

Данная динамика наглядно отслеживается в примере с магнитной крошкой. При расположении магнитной крошки на плоскости, кусочки магнита, преодолевая силы трения, устремляются в единый центр (лавинообразный процесс на практике).

Следует так же отметить, что гипотетически существует некая теоретическая возможность, при которой при целом ряде дополнительных условий, таких как: организованное планетарное движение(притягивающихся) молекул относительно друг друга, отсутствие критических столкновений и прочих факторов способных вывести систему из равновесия модель газа на силах притяжения могла бы быть «жизнеспособной».

И хоть данная вероятность- ничтожна , предположим, что все необходимые условия все же можно соблюсти и рассмотрим модель подробнее.

При каких условиях возможно существование данной модели?

При условии если взаимное расположение связанных взаимодействием объектов (молекул) не будет приводить к образованию лавинообразного процесса. То есть все связанные взаимодействием объекты (молекулы) относительно друг друга в каждый момент времени должны находиться на расстояниях соответствующих балансу сил и двигаться по очень строгим траекториям (подобно как это происходит в модели на силах отталкивания, где местоположение выравнивается за счет сил самой системы). И любое даже минимальное отклонение от баланса сил выведет систему, построенную на притяжении из равновесия , и запустит лавинообразный процесс.

Назовем подобное отклонение критическим для силового баланса.

Взаимоположение тел небесной Механики в силовом смысле является близким аналогом силового взаимодействия в рамках идеальной модели газа.

Вся небесная Механика изначально базируется на предположении, что подобное взаимно уравновешенное силовое взаимодействие небесных тел на силах притяжения возможно и имеет место быть в природе.

И если предполагать, что таковое силовое равновесие на силах притяжения действительно имеет место в природе, то к взаимному расположению тел в пространстве предъявляются довольно строгие требование.

Силовое взаимодействие всех без исключения небесных тел должно протекать в рамках строгого равновесия. При полном недопущении отклонений критических для силового баланса,иначе запускается лавинообразный процесс (подобно как в модели газа построенной на притяжении).

Рассмотрим силовые взаимодействия в рамках Классической Механики.

Силовые взаимодействия в рамках Классической Механики

определяется наличием сил Тяготения и Центробежных сил (Инерции).

( На данном этапе имеет смысл отметить, что некоторые физики пытаются игнорировать/отрицать наличие сил инерции. Подобный подход не является физически состоятельным. Подробное описание данной проблематики приводится в приложении ).

Тело (объект) движется поступательно и равномерно только в одном случае: когда все силы, приложенные к телу, взаимно уравновешены. Так же необходимо помнить, что всякое действие рождает противодействие. В физическом смысле это означает: что если ядро падает на Землю, то и Земля в этот момент падает на ядро. (И не смотря на то, что результат смещения Земли незначителен, сам факт такого смещения имеет место и с физической точки зрения данное явление полностью оправдано).

Поэтому, никакие представления, что в небесной Механике движение отдельно взятого тела якобы независимо и произвольно (от других тел) - не могут быть сколько-либо физически состоятельными.

Перемещение любого даже чрезвычайно малого тела сказывается на расположении тел, участвующих с ним в силовом взаимодействии. А поскольку в силовое взаимодействие взаимно вовлечены все тела небесной Механики, то соответственно и любое перемещение отдельно взятого тела сказывается на взаимном расположении всех остальных тел.

Поскольку в визуальном плане силовую динамику взаимного распределения тел в пространстве, заполненном телами различных размеров, довольно трудно себе представить - воспользуемся для наглядности упрощенной схемой.

Заполним некий заданный объем телами равными по массе и размеру (равноудаленное расположение).

Если мы введем в схему расчетное тело большей массы, то взаимное расположение остальных тел изменится. Вокруг более массивного тела образуется разряженная область, в физическом плане, обеспеченная динамикой выравнивания приложенных к телу сил.

Данная динамика сходится с наблюдениями: чем более массивным является скопление небесных объектов, тем значительнее объем разряженной области, содержащей это скопление объектов. Пример: галактики и окружающие их пространства.

В свою очередь, любое расчётное тело в силовом плане может быть представлено как некая область, заполненная равноудаленными телами равными по массе и размеру.

Планетарное равновесие:

Устойчивость орбиты и равновесие тела на орбите изначально два принципиально разных понятия.

Устойчивость орбиты есть энергетическая характеристика траектории, в принципе не зависящая от фактической направленности приложенных к телу сил ( рис. №14, №15).

Рис№14 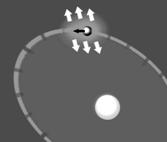Рис№15 №16

В свою очередь, равновесие тела на орбите естьравенство реальных сил,приложенных к телу, находящемуся в отдельно взятой точке орбиты.

На данном этапе имеет смысл отметить, что не все выпускники физических ВУЗов способны различать понятия «Устойчивость орбиты»и « Равновесие тела» на орбите. (Подробное описание данной проблематики приводится в приложении.)

Рассмотрим равновесиев рамках Классической механики:

Равновесие: состояние покоя тела (материальной точки) по отношению к другим телам (применительно к ЗВТ – центрам масс в СО). Равновесие имеет место, когда все действующие на тело силы взаимно уравновешены.

Устойчивое равновесие: когда после малого отклонения от положения тела (относительно источника воздействия), в системе возникают силы, стремящиеся возвратить тело в состояние равновесия, равновесие не нарушается, тело возвращается в положение равновесия, а отклонение от равновесия не возрастает со временем.

Неустойчивое равновесие: когда после малого отклонения положения тела (относительно источника воздействия), равновесие нарушается, тело не возвращается в положение равновесия, а отклонение от равновесия возрастает со временем.

Планетарное равновесие: состояние относительного* покоя центра масс тела по отношению к центру масс другого тела в системе отсчета связанной с центрами масс обоих тел. Планетарное равновесие имеет место, когда все действующие на тело силы взаимно уравновешены.

Планетарное устойчивое равновесие: когда после малого отклонения от положения тела, равновесие не нарушается, тело возвращается в положение равновесия, а отклонение от равновесия не возрастает со временем (Рис № 20, 21, 22). Примерами устойчивого планетарного равновесия являются тела Небесной Механики.

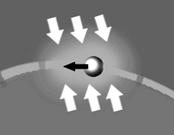
Рис № 20, 21, 22

Планетарное неустойчивое равновесие: когда после малого отклонения от положения тела равновесие нарушается, тело не возвращается в положение равновесия, а отклонение от равновесия возрастает со временем. (Рис № 23, 24, 25)

(примером неустойчивого планетарного равновесия является движение стального шарика по горизонтальной плоскости, вокруг постоянного магнита)

. Рис № 23, 24, 25

· относительный покой тела: состояние покоя относительно избранной системы отсчета, подразумевает возможное изменение геометрического расстояния между центрами масс обоих тел, связанное с продвижением тела по траектории орбиты.

· Первый тип отклонения тела: когда отклонение тела связано с воздействием внешних сил.

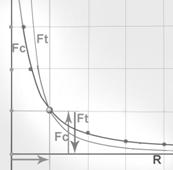· Второй тип отклонения тела: когда отклонение тела связано с продвижением тела по траектории орбиты (некруговой орбиты).

Применительно к обсуждаемой теме (Небесная Механика) речь идет о планетарном устойчивом равновесии, при котором отклонения тела, не вызывает нарушение состояния планетарного равновесия.

Если планетарная система не соответствует исходным определениям Закона Сохранения Энергии, значит такая планетарная система, физически невозможна.

Масса:

Масса – одно из фундаментальных физических понятий.

Масса может быть представлена как 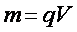произведение объема тела и егоплотности.

В свою очередь размерной базой любого объема тела (равно как и любого объема в Евклидовом пространстве) является произведение трех линейных величин (заданных ортогонально).

Любой объем 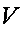может быть представлен как 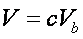произведения некого численного значения 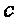и частного объема 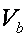, выступающего в качестве размерности.

Частный объем 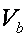, выступающий в качестве размерности, может быть представлен как

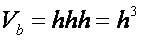, где произведение двух из линейных величин в свою очередь

представляют собой площадь ,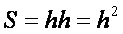

Из чего сам частный объем 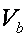, выступающий в качестве размерности, может быть представлен как 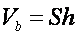произведение площади и линейной величины.

- где площадь 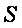может рассматриваться как начальная (нулевая) мера объема (то есть как объем нулевого материального слоя),

- где 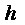(отрезок длины l) может рассматриваться как высота материального слоя.

Для любого тела даже имеющего сложную геометрию, всегда найдется такое частное сечение, площадь которого 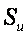, при умножении на сквозное, продольное, линейное сечение тела 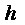(высоту материального слоя тела) - даст значение объема тела равное расчетному

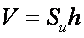(см. рис № 27).

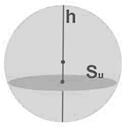рис №27 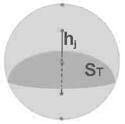рис №28

При этом в качестве 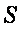при необходимости мы можем использовать площадь 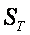стягивающей поверхности в рамках телесного угла (перекрытого расчетным телом), поскольку и для стягивающей поверхности 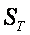всегда найдется такое частное решение h 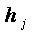, при котором мы получим строгое значение объема 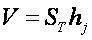(см. рис №28) .

Таким образом масса, выраженная через площадь поверхности, стягивающей телесный угол, образованный данным телом, имеет вид: .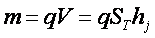

Произведение площади стягивающей поверхности 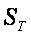и плотности тела 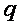применительно к самому телу может быть рассмотрено как начальная (нулевая) мера массы (масса нулевого материального слоя).

Усредненное продольное сечение тела 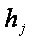(в дальнейшем просто h) может быть рассмотрено как усредненная высота материального слоя.

(Площадь стягивающей поверхности 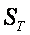в дальнейшем обозначается просто как .)

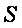Форма Закона Всемирного Тяготения 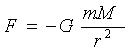может быть представлена

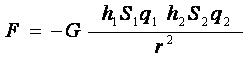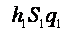в виде: где и 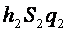есть массы первого и второго тела, (выраженные через площади стягивающих поверхностей).