Силовое обеспечение тяготения от комплекса удаленных объектов.
Рассмотрим процессы, протекающие в частной космологической модели. Допустим, что наша Вселенная на макро уровне равномерно заполнена массами. ( массы распределены равномерно (макро уровень) по всему незамкнутому объему, регламентируемому Евклидовым пространством (см. рис. №29)).
 Рис. № 29
Рис. № 29  Рис. № 30
Рис. № 30
Данная версия в определенной мере (обозримые пределы) совпадает с данными наблюдений полученными для изученной части Вселенной. И если предполагать что и на необозримомудалении во всех областях Вселенной имеет место то же явление (равномерное распределение масс при сходной средней плотности), то мы имеем в любом из направлений от любой точки отсчета – идентичную картину.
В рамках данной версии мы можем вполне уверенно допускать что, задав, некий сквозной стержень определённого сечения и неограниченной продолжительности мы получим для обоих объемов составляющих стержень половин - равное количество масс (распределенных во внутреннем объеме половин данного стержня) и как следствие равное (стремящееся к равному) внешнее воздействие от равноудаленных зон (имеющих равное содержание масс).
Количество этих масс может быть выражено как произведение объема данного стержня (геометрического луча имеющего не нулевоесечение) на среднюю плотность (общего распределения масс во Вселенной).
Средняя плотность Вселенной (наблюдаемой части) нам известна. Объем стержня мы можем задать через его сечение.
Тогда массы половин стержня у нас выражаются в форме равенства:
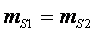 что исходно определяется равенством:
что исходно определяется равенством: 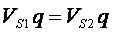
Где 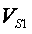 - объем левой половины незамкнутого стержня
- объем левой половины незамкнутого стержня
Где 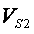 - объем правой половины незамкнутого стержня
- объем правой половины незамкнутого стержня
Где 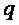 - средняя плотность.
- средняя плотность.
В свою очередь объемы 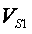 и
и 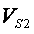 - могут быть представлены как равенство
- могут быть представлены как равенство 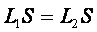
Где 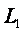 и
и 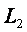 длины половин стержня а
длины половин стержня а 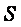 - площадь поперечного сечения стержня.
- площадь поперечного сечения стержня.
Каждая из 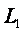 и
и 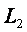 (длин половин стержня) может быть представлена как
(длин половин стержня) может быть представлена как 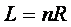
Где 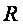 - есть мерный отрезок (линейная величина, избранная по нашему усмотрению)
- есть мерный отрезок (линейная величина, избранная по нашему усмотрению)
Где 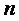 - есть количественный показатель, который мы исходя из поставленной задачи, можем принимать либо как неконечный количественный показатель
- есть количественный показатель, который мы исходя из поставленной задачи, можем принимать либо как неконечный количественный показатель 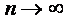 либо как конечный количественный показатель (численное значение).
либо как конечный количественный показатель (численное значение).
Из чего масса каждого фрагмента стержня, имеющего длину 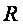 , будет равна
, будет равна 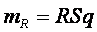 ,
,
а обща масса половины стержня, равна 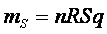
То есть для обеих половин стержня мы имеем равенство масс выражаемое как 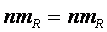
Для удобства вычислений зададим длину мерного отрезка 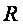 великой настолько, чтобы фрагмент массы самого большого и плотного тела во Вселенной, будучи вырезанным, из тела нашим расчетным стержнем длины R , ни при каких обстоятельствах не превысил общего количественного значения массы, (полученной через среднюю Вселенскую плотность), вырезанное из Вселенной аналогичным стержнем (длины R).
великой настолько, чтобы фрагмент массы самого большого и плотного тела во Вселенной, будучи вырезанным, из тела нашим расчетным стержнем длины R , ни при каких обстоятельствах не превысил общего количественного значения массы, (полученной через среднюю Вселенскую плотность), вырезанное из Вселенной аналогичным стержнем (длины R).
(то есть зададим длину R конечной, но достаточно большой.)
При таких R , равенство 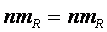 будет корректным для всех расчетных случаев.
будет корректным для всех расчетных случаев.
Расположим в центре нашего сквозного (незамкнутого в обоих направлениях стержня) – материальную точку.
С обеих сторон от неё, в рамках стержня (в рамках данной космологической модели) заключено равное количество масс.
Введем в расчет некое реальное приближающееся, к материальной точке тело (например - Солнце).
В этом случае 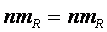 примет вид:
примет вид: 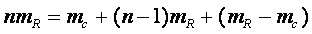
где 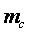 есть часть массы Солнца, вырезанная нашим стержнем (заданного сечения).
есть часть массы Солнца, вырезанная нашим стержнем (заданного сечения).
Если расчетным стержнем, в рамках телесного угла Солнца очертить все направления, то из 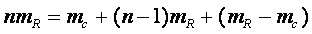 очевидно прослеживается следующая динамика:
очевидно прослеживается следующая динамика:
при разнесении на две самостоятельных сущности комплекса удаленных объектов и нашего приближающегося объекта (Солнца),
Рис. № 31 
- отслеживается расчетное понижение массы одной из половин комплекса удаленных объектов.
Причем, в объемной схеме, данное понижение масс находится не в прямой арифметической зависимости, а в геометрической (от телесного угла и от расстояния между телами).
Подробнее:
Если комплекс удаленных объектов, представить в виденекойудаленной сферыимеющей определенную (конечную, либо незамкнутую с внешней стороны) толщину поверхности,с равномерным распределением массы(и возможностью отдельно взятой массы перемещаться в рамках очерченной области), то:
при отделении от такой модели некой массы (например, Солнца) и перемещении её в сторону центра
- на внутренней поверхности сферы согласно 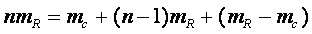 образуется полость. Которая увеличивается по мере приближения расчетного тела к центру сферы.. (см. рис № 32, 33 )
образуется полость. Которая увеличивается по мере приближения расчетного тела к центру сферы.. (см. рис № 32, 33 )
 рис. № 32
рис. № 32 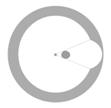 рис. №33
рис. №33
Объем данной полости в геометрическом плане соответствует вогнутомусфероиду.
(в силовом плане сфероид (разницы масс) расположен с противоположной стороны
(См. рис № 34 - 36))
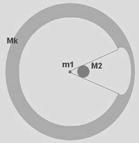 рис. №34
рис. №34 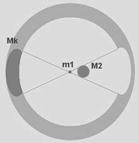 рис. №35
рис. №35 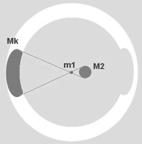 рис. №36
рис. №36
Масса сфероида рассчитывается исходя из:
- объема тела образованного площадью поверхности стягивающей телесный угол, создаваемый приближающимся телом, для расчетного расстояния до комплекса удаленных объектов 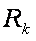 ,
,
- соответствующих линейных сечений приближающегося тела массы 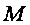 ,
,
- средней плотности рассчитанной для каждого соответствующего сечения приближающегося тела массы М, присвоенной в дальнейшем полученной фигуре соответственно мировым линиям.
Телесный угол – отношение стягивающих поверхностей к квадрату расстояния.
Стягивающие поверхности находятся в зависимости от телесного угла и легко могут быть выражены друг из друга.
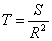 из чего отношение стягивающей поверхности сфероида (разницы масс) комплекса равно отношению стягивающей поверхности тела оказывающего воздействие,к квадрату расстояния
из чего отношение стягивающей поверхности сфероида (разницы масс) комплекса равно отношению стягивающей поверхности тела оказывающего воздействие,к квадрату расстояния 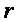 между взаимодействующими телами
между взаимодействующими телами 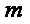 и
и 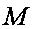
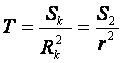
Из чего площадь стягивающей поверхности на комплексе выражается как:
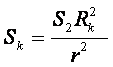 произведение стягивающей поверхности второго тела (Солнца) и расстояния до приведенного к сфере комплекса удаленных объектов, деленное на квадрат расстояния между телами
произведение стягивающей поверхности второго тела (Солнца) и расстояния до приведенного к сфере комплекса удаленных объектов, деленное на квадрат расстояния между телами 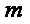 и
и 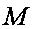 (т. есть между ядром и Солнцем)
(т. есть между ядром и Солнцем)
Из чего наше исходное:
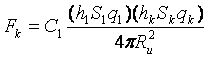 при выражении
при выражении 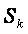 через
через 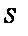 исходя из
исходя из 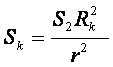
принимает вид: 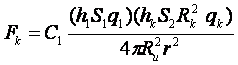 где:
где:
1). расчетная плотность (разницы масс комплекса) 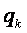 исходя из зависимости
исходя из зависимости
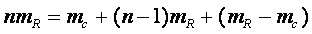 является равной
является равной 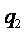 - плотности тела оказывающего воздействие (т.е. Солнца),
- плотности тела оказывающего воздействие (т.е. Солнца),
2) где высота материального слоя 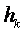 исходя из
исходя из 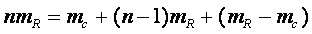
является равной 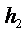 высоте материального слоя тела оказывающего воздействие.
высоте материального слоя тела оказывающего воздействие.
Следовательно 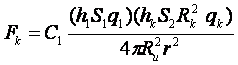 принимает вид
принимает вид
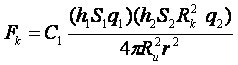
где расстояние до комплекса 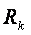 исходя из определения, у нас является
исходя из определения, у нас является 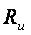 (расстоянию до объекта, оказывающего воздействие) следовательно
(расстоянию до объекта, оказывающего воздействие) следовательно 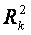 и
и 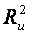 равны (в формуле могут быть сокращены). Следовательно, исходная форма
равны (в формуле могут быть сокращены). Следовательно, исходная форма
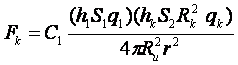 является аналогом формы
является аналогом формы 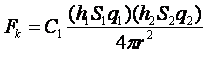 ,
,
которая при вынесении единого коэффициента приобретает вид 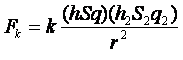
что (за исключением знака перед формулой) является функциональным эквивалентом 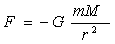 . И если рассматривать тяготение как сумму внешних (от комплекса) и внутренних (от взаимодействия двух тел) сил, то результатом
. И если рассматривать тяготение как сумму внешних (от комплекса) и внутренних (от взаимодействия двух тел) сил, то результатом
будет являться 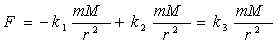 эквивалент общепринятой формы Закона Тяготения.
эквивалент общепринятой формы Закона Тяготения.
При этом отсутствие знака перед формулой «компенсируется» противоположным направлением радиус вектора (направлением извне - от комплекса к пробному телу).
Из чего однозначно следует что:
1) версия комплексного отталкивания соответствует всем без исключения наблюдаемым проявлениям известным как следствия Всемирного Тяготения по версии 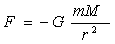 .
.
2) версия комплексного отталкивания в силу эквивалентности формульного выражения - в принципе не может противоречить наблюдаемой картине мира в рамках очерченных редакцией закона 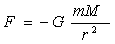 .
.
Таким образом, мы доказали что:
1) Форма 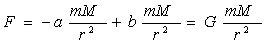 является эквивалентом общепринятой
является эквивалентом общепринятой
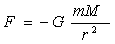 ,
,
2) Закон Всемирного Тяготения по версии комплексного отталкивания имеет вид 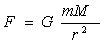 .
.
Дополнительные пояснения и аргументация:
Частную динамику силового взаимодействия можно отследить через равенство результирующей внешней силы (от комплекса удаленных объектов) и силы взаимодействия двух тел.
Подробнее:
Если сравнивать частные значения силы воздействия от комплекса 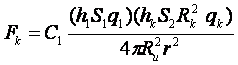
и силы взаимодействия двух тел 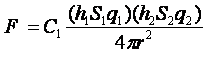 то очевидно, что
то очевидно, что
при 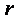 равном
равном 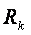 (что соответствует ситуации, когда воздействующее тело
(что соответствует ситуации, когда воздействующее тело 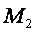 (Солнце) удалено от пробного тела (ядра) на расстояние соответствующее значительному удалению)
(Солнце) удалено от пробного тела (ядра) на расстояние соответствующее значительному удалению)
из 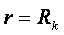 следует равенство силы воздействия комплекса и силы взаимодействия двух тел
следует равенство силы воздействия комплекса и силы взаимодействия двух тел
Поскольку форма
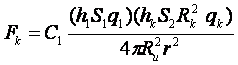 при
при 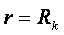 принимает вид
принимает вид 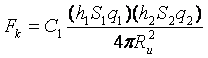
Который полностью соответствует 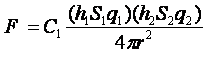 ,из чего следует, что при
,из чего следует, что при 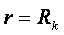 внешние силы (от комплекса удаленных объектов) и силы взаимодействия двух тел будут равны.
внешние силы (от комплекса удаленных объектов) и силы взаимодействия двух тел будут равны.
Что в рамках Классической механики сходится с общепринятыми представлениями.
Сравнение версий тяготения (бытующей версии тяготения Ньютона и комплексной версии тяготения).
Если рассмотреть версию Комплексного Тяготения с учетом воздействий не направленных по линии соединяющей центры масс обоих тел, то явно просматривается различие силовых динамик по пространственным осям.
Комплексное воздействие на тело по оси, соединяющей центры масс обоих тел, значительно меньше.
Данное различие отражено на приведенных ниже схемах (отражающих воздействие от комплекса).
На рисунках № 37 и №38 схематично отражено общее количество масс, определяющее разницу осевых давлений на тело по версии Комплексного Тяготения.
На рисунке № 39 отражена схема внешнего (от комплекса удаленных тел) силового давления на тело по версии Комплексного Тяготения.
 рис. №37
рис. №37 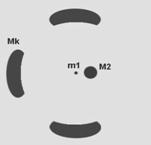 рис. № 38
рис. № 38
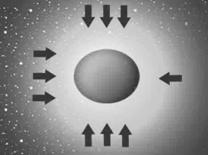 рис. №39
рис. №39 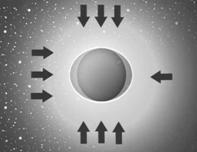 рис. №40
рис. №40
Из приведенных схем, очевидно отслеживается динамика, обеспечивающая силовую составляющую явлений со направленных вектору тяготения.
На рисунке № 39 – схема , определяющая силовое обеспечение замороженного Лунного прилива (геометрическая форма луны).
На рисунке № 40 - схема, определяющая силовое обеспечение приливов (на Земле).
На рисунке № 41- отображена схема, определяющая возгонку хвостов кометы - как следствие воздействия от комплекса удаленных объектов.
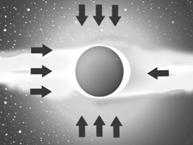 рис. №41
рис. №41 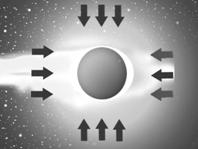 рис. №42
рис. №42
На рисунке № 42 отображена схема, определяющая возгонку хвоста кометы с учетом воздействия от комплекса удаленных объектов и воздействия от Солнца.
В данном случае явление может быть объяснено изменением «спектра» гравитационного воздействия прошедшего через Солнце.
На рисунке № 43 отражена схема силового давления на тело по версии Прямого Тяготения.
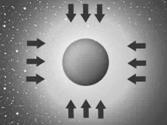 рис. №43
рис. №43
Какой либо неуравновешенный фактор воздействия от комплекса удаленных объектов по версии Прямого Тяготения – отсутствует.
В современной физике в том числе в официально признанных учебных пособиях бытует много интеллектуально несостоятельных воззрений.
Примером может служить точка зрения что: « ближайшая к Солнцу точка Земли (зенит) притягивается чуть сильнее».
Рассмотрим, почему эта точка зрения является ненаучной, и почему приливы по версии прямого тяготения физически – невозможны:
Предположим Земля по прямой падает на Солнце .
Земля находится в свободном падении ( в практической невесомости) и океан принимает форму правильной сферы.
А чем отличается тело на орбите от тела находящегося в состоянии невесомости ?
Принципиально ничем. (точка падения – «уходит» в сторону).
А раз тело в невесомости и сил нет то какие могут быть приливы? По версии прямого тяготения - никакие .
Силу от Солнца приложить к телу второй раз мы права не имеем.
А раз силы нет то и прилив обеспечить не чем.
( кроме того прилив выше возможного расчетного воздействия – официально признано).
По комплексной версии – получается, что отталкивание от комплекса в продольном и поперечных направлениях разное.
В продольном направлении у нас разряженная область и силовое воздействие меньше.
Вода поднимается как раз с двух сторон. С одной больше с другой меньше. Полностью сходится с наблюдениями.
Когда тела притягиваются формула имеет вид: 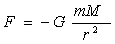 .
.
Когда тела притягивается и при этом что либо деформируется формула должна иметь вид: 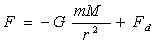 .
.
Дата добавления: 2016-09-06; просмотров: 1495;











