Объединенный закон газового состояния (формула Клапейрона).
При 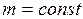
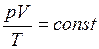 . (II.4)
. (II.4)
Если по условию задачи газ находится при одних каких-либо условиях, то его сравнивают с состоянием данного газа при нормальных условиях:
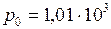 Па,
Па, 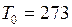 К,
К, 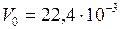 м3 (объем 1 моль любого газа при нормальных условиях).
м3 (объем 1 моль любого газа при нормальных условиях).
Уравнение Клапейрона – Менделеева(универсальное уравнение газового состояния)
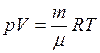 , (II.5)
, (II.5)
где 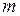 – масса газа;
– масса газа; 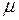 - молярная масса газа;
- молярная масса газа;
R = 8,31 Дж/(моль·К) – постоянная для всех газов величина, называемая молярной газовой постоянной (или универсальной газовой постоянной).
Закон Дальтона. Если в сосуде находится смесь нескольких газов, не вступающих друг с другом в химические реакции, то давление смеси газов равно сумме давлений, производимых каждым газом в отдельности, если бы он один занимал весь сосуд (парциальные давления)
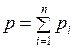 , (II.6)
, (II.6)
где 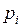 –парциальные давления компонент смеси.
–парциальные давления компонент смеси.
ЗАДАЧА № II.1На диаграмме 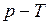 показан замкнутый процесс 1–2–3–1. Изобразите этот процесс на
показан замкнутый процесс 1–2–3–1. Изобразите этот процесс на 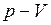 и
и 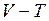 диаграммах.
диаграммах.

|
Ответ:Процесс 1–2 изохорический, так как в нем давление прямо пропорционально температуре; процесс 2–3 – изотермический; процесс 3–1 – изобарический. Данный цикл на 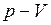 диаграмме и
диаграмме и 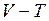 диаграмме будет выглядеть так:
диаграмме будет выглядеть так:



ЗАДАЧА № II.2При нагревании газа получена зависимость давления от температуры (рис.20). Сжимается или расширяется газ во время нагревания ?


Рисунок 20 - Диаграмма 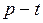 Рисунок 21 – Диаграмма
Рисунок 21 – Диаграмма 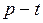
Ответ:Газ расширяется. Если провести изохоры через точки 1 и 2 (рис.21), то легко убедиться, что 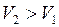 .
.
ЗАДАЧА № II.3На рис.22 изображены две изобары. Какая из изобар соответствует большей массе газа ?
Ответ:Первая, так как при одинаковых давлении и температуре большая масса занимает больший объём.

Рисунок 22 – Две изобары
Ответ:Первая, так как при одинаковых давлении и температуре большая масса занимает больший объём.
ЗАДАЧА № II.4 Под колоколом воздушного насоса стоит банка с водой, в ней пузырек. Как изменяется объем пузырька при откачивании воздуха? Температура постоянная.
Ответ: Объем пузырька увеличивается, т.к. по закону Бойля-Мариотта
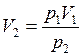 , где
, где 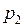 меньше
меньше 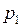 за счет откачки воздуха при постоянном гидростатическом давлении.
за счет откачки воздуха при постоянном гидростатическом давлении.
ЗАДАЧА № II.5 Две колбы с воздухом при нормальном давлении и различные по объему закупоривают и нагревают в парах кипящей воды до 1000 С. Одинаковым ли будет в них давление воздуха после нагревания?
Ответ:Давление будет одинаковым, т.к. в обеих колбах плотности воздуха равны и не изменяются при нагревании 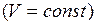 . Из уравнения
. Из уравнения
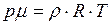 следует, что приращение
следует, что приращение 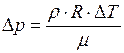 независит от объема колбы.
независит от объема колбы.
ЗАДАЧА № II.6 В газоразрядной плазме (искра, электрическая дуга), состоящей из электронов, ионов, нейтральных атомов и молекул, в разных компонентах разная температура. Почему это возможно?
Ответ: При электрическом разряде процессы протекают очень быстро (меньше времени релаксации), поэтому общая температура не успевает установиться.
ЗАДАЧА № II.7 Найти молярную массу воздуха, считая, что он состоит по массе из одной части кислорода и трех частей азота.
Дано: 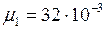 кг/моль;
кг/моль;
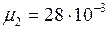 кг/моль;
кг/моль;
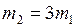 .
.
Найти: 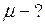
Решение
Воздух, являясь смесью идеальных газов, тоже представляет идеальный газ, и к нему можно применить уравнение Клапейрона-Менделеева
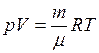 . (1)
. (1)
Для каждой компоненты смеси кислорода и азота запишем соответствующее уравнение:
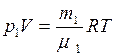 , (2)
, (2)
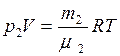 , (3)
, (3)
где 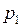 и
и 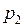 – парциальные давления кислорода и азота.
– парциальные давления кислорода и азота.
По закону Дальтона давление воздуха 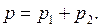 Складывая (2) и (3), получим
Складывая (2) и (3), получим
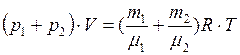 (4)
(4)
Сравнивая (1) и (4) и учитывая, что 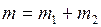 ,имеем
,имеем
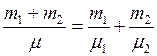 , откуда
, откуда
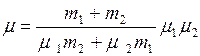 . (5)
. (5)
Подставляя в (5) 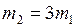 , найдем молярную массу воздуха
, найдем молярную массу воздуха
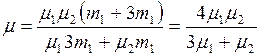 ,
,
Подставляя численные значения, получим 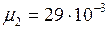 кг/моль.
кг/моль.
ЗАДАЧА № II.8Как изменится давление идеального газа, если его объем и температуру уменьшить в два раза?
Решение
Уравнение Клапейрона – Менделеева приводит к следующему выражению для давления газа
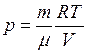 .
.
Если объем 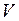 и температуру
и температуру 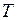 газа уменьшить вдвое, то давление газа, как видно из уравнения, не изменится.
газа уменьшить вдвое, то давление газа, как видно из уравнения, не изменится.
ЗАДАЧА № II.9Объем пузырька воздуха по мере всплывания его со дна озера на поверхность увеличивается в три раза. Какова глубина озера?
Дано: 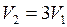 ;
;
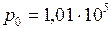 Па;
Па;
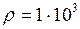 кг/м3.
кг/м3.
Найти: 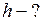
Решение
Считаем, что температура воды в озере на любой глубине постоянна. Тогда по закону Бойля – Мариотта
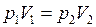 ,
,
где 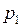 ,
, 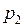 – давление воздуха в пузырьке у дна и поверхности озера соответственно;
– давление воздуха в пузырьке у дна и поверхности озера соответственно;
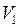 ,
, 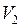 – объемы пузырьков у дна и поверхности озера.
– объемы пузырьков у дна и поверхности озера.
Очевидно, что давление 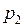 воздуха в пузырьке у поверхности озера равно атмосферному давлению
воздуха в пузырьке у поверхности озера равно атмосферному давлению 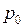 , т.е.
, т.е. 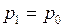 . Тогда
. Тогда 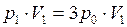 , откуда
, откуда 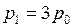 .
.
Следовательно, увеличение давления у дна озера будет
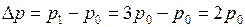
Как известно из гидростатики, 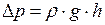
где 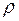 - плотность воды;
- плотность воды;
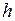 – глубина озера.
– глубина озера.
Приравнивая правые части двух последних уравнений, получим
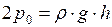
откуда
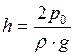 ;
; 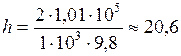 м.
м.
ЗАДАЧА № II.10Сосуд вместимостью 20 л, заполненный воздухом при давлении 0,4 МПа, соединяют с сосудом, из которого воздух удалён. При этом давление в обоих сосудах становится одинаковым и равным 1,0·105 Па. Определить вместимость второго сосуда. Процесс изотермический.
Дано: 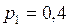 МПа
МПа 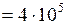 Па;
Па;
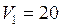 л
л 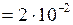 м3;
м3;
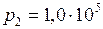 Па.
Па.
Найти: 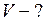
Решение
Изотермический процесс протекает при постоянной температуре 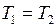 и подчиняется закону Бойля – Мариотта, для которого справедливо уравнение (II.1), или
и подчиняется закону Бойля – Мариотта, для которого справедливо уравнение (II.1), или 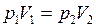 . Но после присоединения второго сосуда газ занял объём
. Но после присоединения второго сосуда газ занял объём 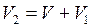 , следовательно,
, следовательно, 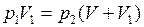 , или
, или
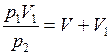 , откуда
, откуда 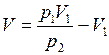 ; Подстановка численных данных
; Подстановка численных данных
дает 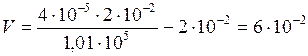 м3 . Вместимость второго сосуда
м3 . Вместимость второго сосуда 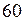 л.
л.
ЗАДАЧА № II.11Изменение состояния идеального газа описывается приведенным графиком (рис.23). Как изменяется температура при переходе газа из состояния 1 в состояние 3?

Рисунок 23 - График зависимости давления от объёма
Решение
При переходе газа из состояния 1 в состояние 2 ( 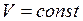 - изохорный процесс), давление газа увеличилось в 2 раза. Следовательно, температура возросла вдвое. При переходе из состояния 2 в состояние 3 (
- изохорный процесс), давление газа увеличилось в 2 раза. Следовательно, температура возросла вдвое. При переходе из состояния 2 в состояние 3 ( 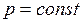 – изобарный процесс), объем газа увеличился в 3 раза. Это возможно при возрастании температуры еще в 3 раза. Таким образом, переходу (1-3) соответствует повышение абсолютной температуры в 6 раз.
– изобарный процесс), объем газа увеличился в 3 раза. Это возможно при возрастании температуры еще в 3 раза. Таким образом, переходу (1-3) соответствует повышение абсолютной температуры в 6 раз.
ЗАДАЧА № II.12 При какой температуре находился газ, если в результате изобарного нагревания на 1К его объём увеличился на 3,5·10-3 от первоначального?
Дано: 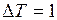 К;
К;
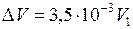 ;
;
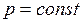 .
.
Найти: 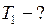
Решение
В результате нагревания температура газа повысилась на 1К, следовательно, 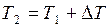 . При этом объём газа увеличился от V1 до V2, т.е.
. При этом объём газа увеличился от V1 до V2, т.е. 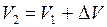 . Так как процесс протекает при постоянном давлении р2=р1, то уравнение состояния
. Так как процесс протекает при постоянном давлении р2=р1, то уравнение состояния 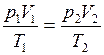 преобразуется
преобразуется 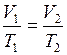 , или
, или
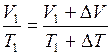 . Решение этого уравнения относительно Т1 дает
. Решение этого уравнения относительно Т1 дает
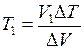 .
.
Подстановкой численных значений получим:
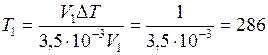 К.
К.
ЗАДАЧА № II.13В баллоне находится идеальный газ. Когда часть газа выпустили, температура газа в баллоне уменьшилась в 3 раза, а давление – в 4 раза. Какую часть газа (в процентах) выпустили?
Дано: 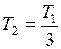 ;
;
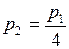 ;
;
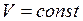 .
.
Найти: 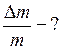
Решение
Для двух описанных ситуаций уравнение состояния имеют вид
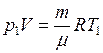 (1)
(1)
и 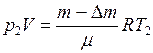 , (2)
, (2)
где 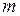 – начальная масса газа,
– начальная масса газа, 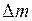 - выпущенная из баллона масса газа. Объём баллона V не изменялся. Выразим объем из (1) уравнения
- выпущенная из баллона масса газа. Объём баллона V не изменялся. Выразим объем из (1) уравнения 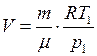 и подставим в (2), в результате получим
и подставим в (2), в результате получим 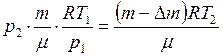 . Сократив одинаковые сомножители и поделив обе части уравнения на
. Сократив одинаковые сомножители и поделив обе части уравнения на 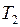 и на
и на 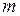 , получим
, получим 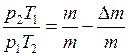 , откуда
, откуда 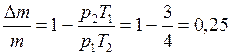 . Следовательно, из баллона выпустили 25% газа.
. Следовательно, из баллона выпустили 25% газа.
ЗАДАЧА № II.14На рис.24 показаны две изохоры для газа одной и той же массы. Углы наклона изохор к оси абсцисс равны 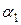 и
и 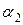 . Как соотносятся эти объёмы газа?
. Как соотносятся эти объёмы газа?

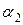
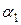
Рисунок 24 - График двух изохор для газа одной и той же массы
Решение
Уравнения состояния позволяют записать для двух разных объёмов взаимосвязь параметров 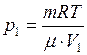 (1) и
(1) и 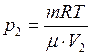 (2)
(2)
При некоторой температуре из графика (см. рис.24) определим, что 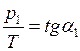 , а
, а 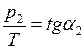 . Тогда уравнения (1) и (2) примут вид
. Тогда уравнения (1) и (2) примут вид
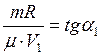 , (3)
, (3)
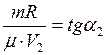 . (4)
. (4)
Поделив уравнение (3) на (4), получим искомое соотношение объемов
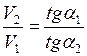 .
.
ЗАДАЧА № II.15Давление воздуха внутри бутылки, закрытой пробкой равно 0,1 МПа при температуре 7 0С. На сколько градусов нужно нагреть воздух в бутылке, чтобы пробка вылетела? Без нагревания пробку можно вынуть, прикладывая к ней силу 30 Н. Поперечное сечение пробки 2 см2.
Дано: 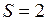 см2
см2 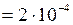 м2;
м2;
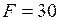 H;
H;
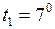 C;
C; 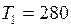 К;
К;
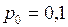 МПа
МПа 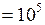 Па.
Па.
Найти: 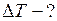
Решение
Чтобы пробка вылетела из бутылки, необходимо, чтобы давление воздуха в бутылке равнялось 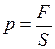 . При нагревании объём не изменяется. По закону Шарля
. При нагревании объём не изменяется. По закону Шарля 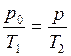 , откуда
, откуда 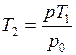 , следовательно,
, следовательно, 
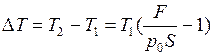 . Подстановка численных значений дает
. Подстановка численных значений дает 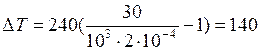 К.
К.
Для того чтобы пробка вылетела из бутылки, необходимо воздух в ней нагреть на 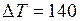 К.
К.
ЗАДАЧА № II.16Начертите график зависимости плотности газа от температуры при изобарическом процессе и зависимости плотности газа от давления при изотермическом процессе, 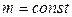 .
.
Решение
Согласно уравнению Клапейрона – Менделеева 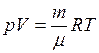 . Плотность газа
. Плотность газа 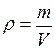 , откуда
, откуда 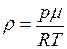 . Если
. Если 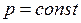 , то
, то 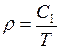 , где
, где 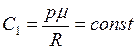 .
.
Следовательно, зависимость 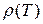 имеет вид гиперболы (рис.25). Если
имеет вид гиперболы (рис.25). Если 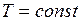 , то
, то 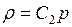 , где
, где 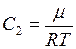 , следовательно, плотность изменяется по линейному закону (рис.26).
, следовательно, плотность изменяется по линейному закону (рис.26).


Рисунок 25 - Зависимость плотности Рисунок 26 - Зависимость плотности
от температуры от давления
ЗАДАЧА № II.17Имеется смесь из 4,4·1021 молекул кислорода, 0,9·1021 молекул углекислоты и 2,1·10 21 молекул азота. Найти давление этой смеси на стенки сосуда емкостью 2 л, если сосуд нагрет до 200С, и молекулярную массу смеси.
Дано: 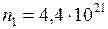 ;
; 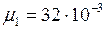 кг/моль;
кг/моль;
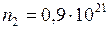 ;
; 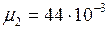 кг/моль;
кг/моль;
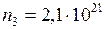 ;
; 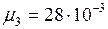 кг/моль;
кг/моль;
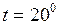 C;
C; 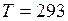 K;
K; 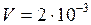 м3.
м3.
Найти: 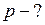
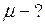
Решение
Из уравнения Клапейрона - Менделеева 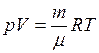 выразим давление
выразим давление
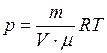 . (1)
. (1)
Парциальные давления кислорода, углекислоты и азота равны
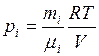 (2)
(2)
где 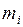 и
и 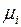 – масса и молярная масса отдельного газа. Выразим массу газа
– масса и молярная масса отдельного газа. Выразим массу газа
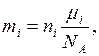 где
где 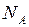 – число Авогадро и подставим в (2)
– число Авогадро и подставим в (2)
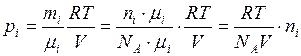 .
.
Давление смеси газов можно рассчитать по закону Дальтона (3)
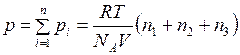 , (4)
, (4)
где 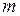 и
и 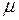 – масса и молярная масса смеси.
– масса и молярная масса смеси.
Подстановка численных значений дает
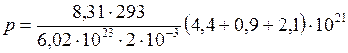
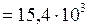 Па.
Па. 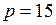 кПа.
кПа.
Приравняв правые части уравнений (2) и (4), получим
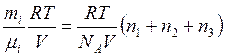 , откуда
, откуда
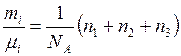 . (5)
. (5)
Массу газа 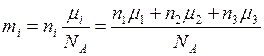 подставим в (5) и получим
подставим в (5) и получим
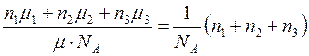 , отсюда
, отсюда
определим молярную массу смеси
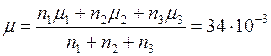 кг/моль.
кг/моль.
§II.1.2ОСНОВЫ МОЛЕКУЛЯРНО - КИНЕТИЧЕСКОЙ ТЕОРИИ ГАЗОВ
Все вещества состоят из атомов и молекул. Для измерения количества вещества вводится единица – моль. В моле любого вещества содержится одинаковое число молекул 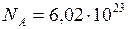 моль–1, называемое постоянной Авогадро.
моль–1, называемое постоянной Авогадро.
Все молекулы находятся в непрерывном хаотическом движении, которое называется тепловым.
Молекулы газа обладают средней кинетической энергией поступательного движения
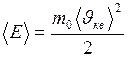 , (II.7)
, (II.7)
где 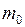 – масса одной молекулы;
– масса одной молекулы;
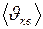 - средняя квадратичная скорость поступательного движения молекул.
- средняя квадратичная скорость поступательного движения молекул.
Согласно молекулярно – кинетической теории, эта энергия связана с термодинамической температурой соотношением
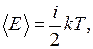 (II.8)
(II.8)
где 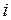 – сумма поступательных и вращательных степеней свободы;
– сумма поступательных и вращательных степеней свободы;
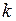 – постоянная Больцмана;
– постоянная Больцмана;
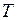 – термодинамическая температура газа.
– термодинамическая температура газа.
Зависимость давления газа от концентрации молекул и температуры
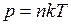 (II.9)
(II.9)
ЗАДАЧА № II.18Какой импульс передает молекула стенке сосуда, если, падая перпендикулярно к стенке: 1) отразится упруго с той же скоростью;
2) прилипнет к стенке? Масса молекулы 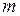 , скорость
, скорость 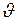 .
.
Ответ:1) 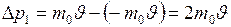 2)
2) 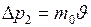 .
.
ЗАДАЧА № II.19Какие молекулы в атмосфере движутся быстрее: молекулы кислорода или азота?
Ответ:Молекулы азота, так как 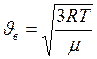 , а
, а 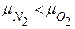 .
.
ЗАДАЧА № II.20 Водород и кислород равной массы помещены в цилиндры со свободно перемещающимися поршнями. Чем будут отличаться изобары этих газов?
Ответ: Поскольку молекулы водорода и кислорода двухатомные, то при одной и той же температуре их средние кинетические энергии 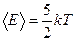 будут одинаковые. Однако, молекул водорода при одинаковых массах и объемов больше, поэтому водород создает большее давление. А для того чтобы давление было одинаковым, объём занимаемый кислородом, необходимо уменьшить в 16 раз
будут одинаковые. Однако, молекул водорода при одинаковых массах и объемов больше, поэтому водород создает большее давление. А для того чтобы давление было одинаковым, объём занимаемый кислородом, необходимо уменьшить в 16 раз 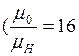 ).
).
ЗАДАЧА № II.21Запуск искусственных спутников показал, что температура воздуха на высоте 1000 км достигает нескольких тысяч градусов. Почему же не расплавляется спутник, двигаясь на этой высоте? Температура плавления железа 15200С.
Ответ:Из-за большой разреженности воздуха на высоте 1000 км он не может передать спутнику то количество теплоты, которое необходимо для его плавления.
ЗАДАЧА № II.22Средняя кинетическая энергия молекул газа при температуре Т зависит от их структуры, что связано с возможностью различных видов движения атомов в молекуле. При условии, что имеют место только поступательное и вращательное движение, определить среднюю энергию молекул водяного пара (Н2О).
Ответ: Средняя кинетическая энергия любой молекулы 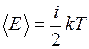 . Молекула водяного пара многоатомная и имеет степеней свободы i = 6 (3 поступательных + 3 вращательных). Средняя энергия, приходящаяся на одну степень свободы
. Молекула водяного пара многоатомная и имеет степеней свободы i = 6 (3 поступательных + 3 вращательных). Средняя энергия, приходящаяся на одну степень свободы 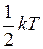 . Следовательно,
. Следовательно, 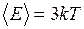 .
.
ЗАДАЧА № II.23Для молекулы воды (Н2О) имеют место все виды движения. Чему равно число степеней свободы для такой молекулы?
Ответ: i = 9 (3 поступательных + 3 вращательных + 3 колебательных).
ЗАДАЧА № II.24Чему равно число степеней свободы для атомарного водорода?
Ответ: i = 3 (поступательных, вращательных и колебательных нет).
ЗАДАЧА № II.25Сколько молекул содержится в стакане воды?
Дано: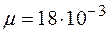 кг/моль ;
кг/моль ;
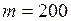 г
г 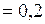 кг;
кг;
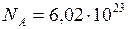 моль–1 .
моль–1 .
Найти: 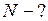
Решение
Учитывая, что в моле находится 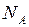 молекул, находим
молекул, находим
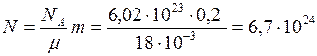 молекул.
молекул.
ЗАДАЧА № II.26Плотность некоторого газа равна6·10–2 кг/м3, средняя квадратичная скорость молекул этого газа 500 м/с. Определить давление, которое газ оказывает на стенку сосуда.
Дано: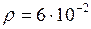 кг/м3;
кг/м3;
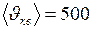 м/с.
м/с.
Найти: 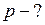
Решение
Восновном уравнении молекулярно-кинетической теории
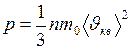 .
.
Произведение 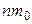 выражает массу молекул, содержащихся в единице объема вещества и, следовательно, равно плотности газа
выражает массу молекул, содержащихся в единице объема вещества и, следовательно, равно плотности газа 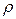 .Таким образом,
.Таким образом,
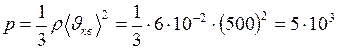 Па.
Па.
ЗАДАЧА № II.27Определить среднюю квадратичную скорость молекул кислорода при 200С. При какой температуре эта скорость равна 500 м/с?
Дано: 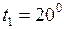 C;
C; 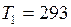 К;
К;
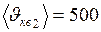 м/с;
м/с;
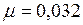 кг/моль.
кг/моль.
Найти: 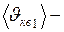 ?
? 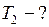
Решение
Кинетическая энергия одной молекулы газа равна
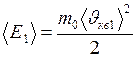 .
.
Согласно молекулярно – кинетической теории, средняя кинетическая энергия поступательного движения одной молекулы газа
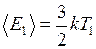
Приравнивая правые части данных уравнений, получаем выражение для скорости
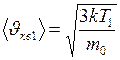 .
.
Так как 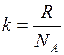 то уравнение для скорости, можно переписать в виде
то уравнение для скорости, можно переписать в виде
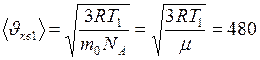 м/с.
м/с.
Запишем уравнение для 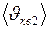 :
: 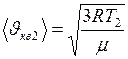 и выразим из него
и выразим из него 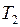 :
: 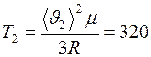 К.
К.
ЗАДАЧА № II.28 В сосуде емкостью 3,5 л находится смесь газов, в которую входит 2·1015 молекул кислорода, 5·1015 молекул азота и 6,6·10-7г аргона. Какова температура смеси, если давление в сосуде 1,74·10-4 мм.рт.ст.?
Дано: 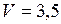 л
л 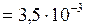 м3;
м3;
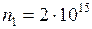 ;
;
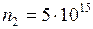 ;
;
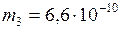 кг;
кг;
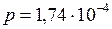 мм.рт.ст.
мм.рт.ст. 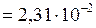 Па;
Па;
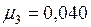 кг/моль.
кг/моль.
Найти: 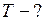
Решение
Для нахождения температуры смеси можно использовать зависимость давления газа от концентрации молекул и температуры
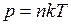 .
.
На основании закона Дальтона
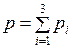 ,
,
где 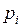 – парциальное давление
– парциальное давление 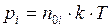 ;
; 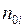 – концентрация
– концентрация 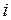 –того газа;
–того газа; 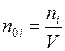 ;
; 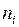 – число молекул
– число молекул 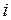 – того газа.
– того газа.
Для аргона 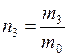 (
( 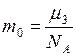 – масса одной молекулы аргона.) Тогда
– масса одной молекулы аргона.) Тогда
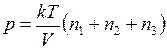
Отсюда искомая температура
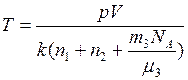 .
. 
Подставляя численные значения и проведя расчет, получим 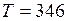 К.
К.
ЗАДАЧА № II.29Оцените число молекул воздуха, падающих на 1 см2 стены комнаты за 1 с. Атмосферное давление 1,01·10 5 Па. Температура окружающей среды 27 0С, молярная масса воздуха 0,029 кг/моль.
Дано: 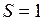 см2
см2 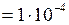 м2;
м2;
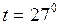 C;
C; 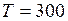 К;
К;
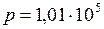 Па.
Па.
Найти: 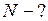
Решение
Согласно уравнению (II.9), концентрация молекул воздуха
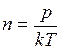 .
.  (1)
(1)
Число молекул, ударяющихся о стенку за 1 с
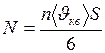 , (2)
, (2)
где среднеквадратичная скорость 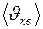
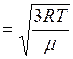 , а число 6 в знаменателе означает
, а число 6 в знаменателе означает 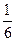 направлений в пространстве. Подставляя (1) в (2) , получим
направлений в пространстве. Подставляя (1) в (2) , получим
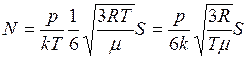 ;
; 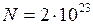 с-1.
с-1.
ЗАДАЧА № II.30Откаченная лампа накаливания объёмом 10 см3 имеет трещину, в которую проникает 106 частиц газа за 1с. Сколько времени понадобится, чтобы в лампе установилось нормальное давление? Температура 0 0С.
Дано: 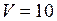 см3
см3 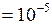 м3;
м3;
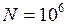 c – 1;
c – 1;
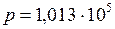 Па;
Па; 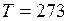 К.
К.
Найти: 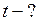
Решение
В лампе при нормальном давлении находится 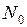 число молекул
число молекул
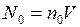 ,
,
где 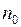 – концентрация молекул, определяемая из уравнения
– концентрация молекул, определяемая из уравнения 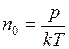 . Тогда число молекул будет равно
. Тогда число молекул будет равно 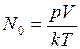 .
.
Считая скорость проникновения молекул в сосуд постоянной, определим время
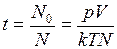 ,
, 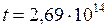 с.
с.
ЗАДАЧА № II.31Два сосуда, содержащие два разных газа, соединены трубкой с краном. Давление в сосудах 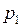 и
и 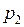 , число молекул
, число молекул 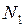 и
и 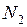 . Определить давление в сосудах, если открыть кран. Температура постоянна.
. Определить давление в сосудах, если открыть кран. Температура постоянна.
Дано: 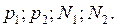
Найти: 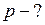
Решение
Давление в первом сосуде определяется выражением 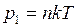 , где
, где 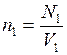 , следовательно,
, следовательно,
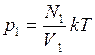 , (1)
, (1)
а во втором сосуде 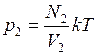 . (2)
. (2)
После того как откроют кран, газы будут иметь общий объем 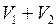 , а давление станет равно
, а давление станет равно
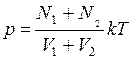 . (3)
. (3)
Выразим из (1) 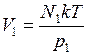 , и из (2)
, и из (2) 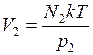 .
.
Подставив в формулу (3) для 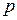 , получим
, получим 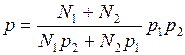 .
.
ЗАДАЧА № II.32Смесь азота и гелия при температуре 270С находится под давлением 1,3·102 Па. Масса азота составляет 70 % от общей массы смеси. Найти концентрацию молекул каждого из газов.
Дано: 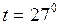 C;
C; 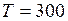 К;
К;
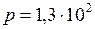 Па;
Па;
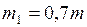 ;
; 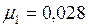 кг/моль;
кг/моль;
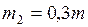 ;
; 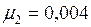 кг/моль.
кг/моль.
Найти: 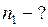
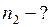
Решение
Из уравнения 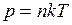 , найдем концентрацию молекул смеси
, найдем концентрацию молекул смеси 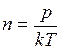 . Массы каждого из газов равны
. Массы каждого из газов равны
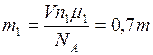 , (1)
, (1)
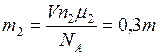 ,(2)
,(2)
где 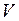 – объём газа. Поделив (1) на (2), найдем отношение концентраций
– объём газа. Поделив (1) на (2), найдем отношение концентраций
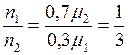 , отсюда
, отсюда 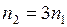 ,а так как
,а так как 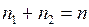 , то
, то
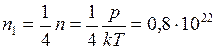 м-3; а
м-3; а 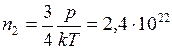 м-3.
м-3.
Дата добавления: 2016-09-06; просмотров: 6496;











