II.1.4 ФИЗИЧЕСКАЯ КИНЕТИКА
Средняя длина свободного пробега молекул газа
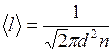 ,(II.17)
,(II.17)
где 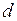 – эффективный диаметр молекул;
– эффективный диаметр молекул;
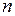 − концентрация молекул.
− концентрация молекул.
Среднее число столкновений одной молекулы в единицу времени
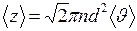 . (II.18)
. (II.18)
Общее число столкновений всех молекул в единице объема за единицу времени
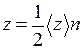 . (II.19)
. (II.19)
Число молекул, ударяющихся за единицу времени в единичную площадку, которая помещена в газе
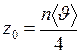 . (II.20)
. (II.20)
Закон диффузии (закон Фика): масса определенного компонента газа( 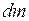 ), диффундирующая за время (
), диффундирующая за время ( 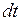 )через площадку (
)через площадку ( 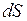 ), расположенную перпендикулярно оси х
), расположенную перпендикулярно оси х
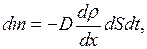 (II.21)
(II.21)
где 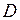 – коэффициент диффузии;
– коэффициент диффузии;
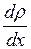 − градиент плотности.
− градиент плотности.
Знак минус обусловлен тем, что перенос массы происходит в направлении убывания плотности.
Коэффициент диффузии
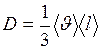 . (II.22)
. (II.22)
Закон теплопроводности ( закон Фурье): количество теплоты ( 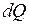 ), переносимое за время (
), переносимое за время ( 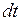 ) через площадку (
) через площадку ( 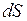 ), расположенную перпендикулярно оси
), расположенную перпендикулярно оси 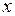
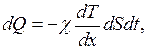 (II.23)
(II.23)
где 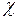 − коэффициент теплопроводности;
− коэффициент теплопроводности;
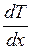 − градиент температуры;
− градиент температуры;
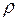 - плотность газа.
- плотность газа.
Знак минус означает, что перенос внутренней энергии происходит в направлении убывания температуры.
Коэффициент теплопроводности
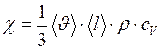 , (II.24)
, (II.24)
где 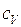 – удельная теплоемкость газа при постоянном объеме.
– удельная теплоемкость газа при постоянном объеме.
Закон вязкости (закон Ньютона): сила внутреннего трения ( 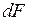 ) между двумя слоями площадью (
) между двумя слоями площадью ( 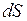 ), движущимися с различными скоростями
), движущимися с различными скоростями
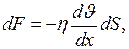 (II.25)
(II.25)
где 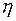 - коэффициент динамической вязкости;
- коэффициент динамической вязкости;
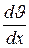 − градиент скорости течения газа в направлении, перпендикулярном к площадке
− градиент скорости течения газа в направлении, перпендикулярном к площадке 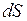 .
.
Знак минус означает, что сила трения, действующая на более быстро движущиеся слои, направлена против скорости.
Коэффициент динамической вязкости
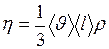 . (II.26)
. (II.26)
ЗАДАЧА № II.48Чем объяснить, что при высокой средней скорости хаотического движения газовых молекул (для воздуха 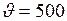 м/с) возникшая в газе разница температур выравнивается сравнительно медленно (т.е. теплопроводность газов мала).
м/с) возникшая в газе разница температур выравнивается сравнительно медленно (т.е. теплопроводность газов мала).
Ответ:При обычном давлении длина свободного пробега молекул газа мала и энергия теплового движения передается молекулами от слоя к слою через очень большое число столкновений, что и замедляет передачу тепла.
ЗАДАЧА № II.49Для чего в сосуде Дьюара создают вакуум?
Ответ:В плотном газе теплопроводность не зависит от давления. Когда создается вакуум (ультраразряженный газ) толщина слоя воздуха между стенками сосуда оказывается равна или меньше длины свободного пробега, и молекулы между собой не сталкиваются. В этом случае теплопроводность пропорциональна концентрации молекул, а, следовательно, и давлению газа. Чем разряженнее воздух, тем меньше теплопроводность.
ЗАДАЧА № II.50Коэффициенты теплопроводности газов имеют следующие значения
Водород 4,2 ·106 Вт/м·град
Гелий 3,4 ·106 Вт/м·град
Кислород 0,57 ·106 Вт/м·град
Углекислый газ 0,34 ·106 Вт/м·град
Какой газ выгоднее использовать для охлаждения? Какой для теплоизоляции?
Ответ:Для охлаждения выгоднее использовать водород (быстрее забирает тепло), для теплоизоляции – углекислый газ (медленнее уходит тепло).
ЗАДАЧА № II.51Почему при резком движении в неподвижном воздухе чувствуется ветер?
Ответ:Ощущение ветра возникает в результате действия силы трения из-за появления градиента скоростей в прилегающем воздухе.
ЗАДАЧА № II.52Почему в закрытом помещении возникший снаружи резкий запах начинает чувствоваться?
Ответ:Вматериале стен и окон имеются узкие щели и поры, через которые в результате диффузии молекулы вещества, вызвавшего запах, проникают в помещение.
ЗАДАЧА № II.53Почему в горячей воде сахар растворяется быстрее, чем в холодной?
Ответ:С увеличение температуры возрастает скорость хаотического движения, а следовательно увеличивается скорость диффузии молекул сахара.
ЗАДАЧА № II.54Как изменится эффективный диаметр молекул газа при изохорическом увеличении давления?
Ответ: Уменьшится, т.к. он убывает с ростом температуры.
ЗАДАЧА № II.55Какое явление имеет место при наличии градиента скорости слоев жидкости или газа?
Ответ: Явление внутреннего трения.
ЗАДАЧА № II.56В потоке жидкости, направленном вдоль оси х, скорость жидкости растет в положительном направлении оси у. В каком направлении происходит перенос импульса направленного движения?
Ответ: В отрицательном направлении оси 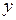 .
.
ЗАДАЧА № II.57Стальной стержень длиной 40 см и площадью поперечного сечения 6 см2 нагревается так, что с одного конца его температура поддерживается 3500С, а с другого находится лед при 00С. Считая, что передача теплоты осуществляется лишь вдоль стержня, подсчитать массу льда, растаявшего за 6 мин. Коэффициент теплопроводности стали 67,2 Дж/(град·м·с).
Дано: 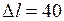 см
см 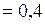 м ;
м ;
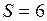 см2
см2 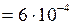 м2;
м2;
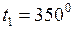 С;
С; 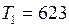 К;
К;
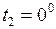 С;
С; 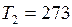 K;
K;
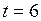 мин
мин 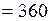 с;
с;
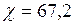 Дж/(град·м·с);
Дж/(град·м·с);
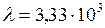 Дж/кг.
Дж/кг.
Найти: 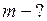
Решение
Количество теплоты, переданной через какое либо сечение стержня от нагретого конца к холодному за время t, определяется на основании закона Фурье (II.23). Для нашего случая этот закон можно представить в виде
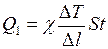 ,
,
где 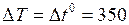 К.
К.
Лед у холодного конца плавится. На плавление данной массы льда тратится энергия
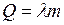 ,
,
где 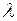 – удельная теплота плавления льда.
– удельная теплота плавления льда.
Так как 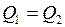 , то для массы льда (
, то для массы льда ( 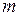 ) получим
) получим
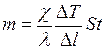 ;
;
Подстановка численных значений дает 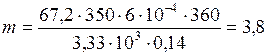 кг.
кг.
ЗАДАЧА № II.58Рассчитать среднюю длину свободного пробега молекул азота, коэффициент диффузии и вязкость при давлении 10 5 Па и температуре 17 0С. Как изменятся найденные величины в результате двукратного увеличения объёма газа: а) при постоянном давлении; б) при постоянной температуре? Эффективный диаметр молекул азота 3,7·10 –8 см.
Дано: 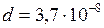 см
см 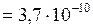 м;
м;
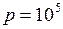 Па;
Па;
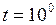 С;
С; 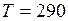 К;
К;
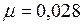 кг/моль
кг/моль
Найти: 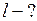
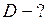
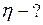
Решение
Средняя длина свободного пробега может быть рассчитана по формуле
 ,
,
где 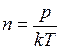 . Тогда
. Тогда 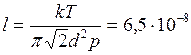 м.
м.
Для расчёта коэффициента диффузии по формуле: 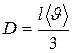 , воспользуемся полученным результатом, определив предварительно среднюю скорость
, воспользуемся полученным результатом, определив предварительно среднюю скорость
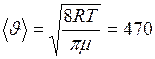 м/с. Тогда
м/с. Тогда 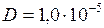 м2/с. Коэффициент вязкости
м2/с. Коэффициент вязкости
рассчитаем по формуле
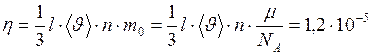 кг/(м∙с)
кг/(м∙с)
Как видно из формулы, средняя длина свободного пробега зависит только от концентрации молекул. При двукратном увеличении объёма концентрация уменьшается вдвое. Следовательно, при любом процессе 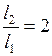 . Индексы 1 и 2 соответствуют состояниям до, и после расширения газа.
. Индексы 1 и 2 соответствуют состояниям до, и после расширения газа.
В выражение коэффициента диффузии входит не только длина свободного пробега, но и средняя скорость. Следовательно, 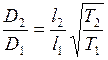 .
.
При постоянном давлении объём прямо пропорционален термодинамической температуре: 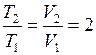 . Таким образом,
. Таким образом, 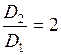 . Вязкость, зависит только от скорости молекул, следовательно, и от
. Вязкость, зависит только от скорости молекул, следовательно, и от
температуры, т.е. 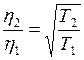 . Это значит, что при постоянном давлении
. Это значит, что при постоянном давлении 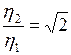 . При постоянной температуре коэффициент
. При постоянной температуре коэффициент 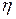 не изменяется.
не изменяется.
ЗАДАЧА № II.59На высоте 20 см над горизонтальной трансмиссионной лентой, движущейся со скоростью 70 м/с, параллельно ей подвешена пластинка площадью 4 см2. Какую силу надо приложить к этой пластинке, чтобы она оставалась неподвижной? Вязкость воздуха при нормальных условиях 1,7·10 –5кг/(м·с). В условиях опыта температура 27 0С, давление атмосферное (рис. 29).
Дано: 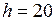 см
см 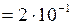 м;
м;
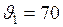 м/с;
м/с;
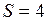 см2
см2 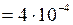 м2;
м2;
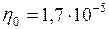 кг/(м·с);
кг/(м·с);
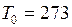 К;
К;
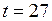 0C;
0C; 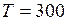 К.
К.
Найти: 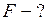
Решение
Благодаря явлению внутреннего трения на слой воздуха, примыкающий к пластинке (адсорбированный пластинкой), действует со стороны движущихся слоёв сила трения. Пластинка будет неподвижна, если приложенная сила F и сила трения Fтр скомпенсированы
F = – Fтр, или в скалярном виде 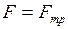 .
.

h
Рисунок 29 - Рисунок к задаче № II.59
Сила трения может быть найдена из закона Ньютона 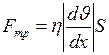 ,
,
где 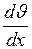 – производная скорости
– производная скорости 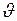 направленного движения слоя по координате х, причём ось Ох перпендикулярна плоскостям трансмиссии и пластинки и направлена от трансмиссии к пластинке.
направленного движения слоя по координате х, причём ось Ох перпендикулярна плоскостям трансмиссии и пластинки и направлена от трансмиссии к пластинке.
По условию задачи, давление атмосферное, это значит, что длина свободного пробега молекул много меньше расстояния h, поэтому вязкость может быть рассчитана по формуле
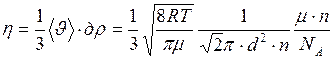 .
.
Здесь 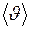 – средняя скорость теплового движения молекул;
– средняя скорость теплового движения молекул;
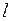 – средняя длина свободного пробега молекул ;
– средняя длина свободного пробега молекул ; 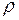 – плотность газа.
– плотность газа.
Как видно, вязкость зависит только от природы газа (эффективного диаметра молекул 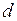 , молярной массы
, молярной массы 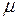 ) и температуры. Поэтому во всём пространстве между трансмиссией и пластинкой
) и температуры. Поэтому во всём пространстве между трансмиссией и пластинкой 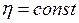 и значение
и значение 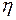 при заданных условиях связано со значением
при заданных условиях связано со значением 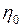 при нормальных условиях соотношением
при нормальных условиях соотношением 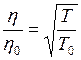 , отсюда
, отсюда 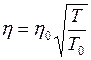 .
.
Из закона сохранения импульса следует, что сила трения, действующая на любой из этих промежуточных слоёв, должна быть одинаковой, следовательно, 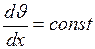 и значение этой производной может быть определено из граничных условий. Так как
и значение этой производной может быть определено из граничных условий. Так как 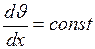 , её можно заменить отношением изменения скорости
, её можно заменить отношением изменения скорости 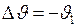 ,
, 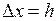 . Тогда
. Тогда 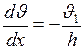 (как и следовало ожидать, производная
(как и следовало ожидать, производная 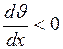 ). Подставляя значения
). Подставляя значения 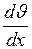 и
и 
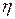 в формулу для силы, получим
в формулу для силы, получим
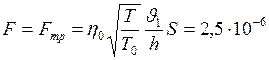 Н.
Н.
| |
§II.2.1 ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ
Первое начало термодинамики имеет вид
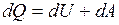 , (II.27)
, (II.27)
где 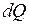 – количество теплоты, подводимое к системе;
– количество теплоты, подводимое к системе;
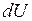 – приращение внутренней энергии системы;
– приращение внутренней энергии системы;
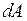 – работа, совершаемая системой против внешних сил.
– работа, совершаемая системой против внешних сил.
Изменение внутренней энергии идеального газа
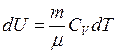 , (II.28)
, (II.28)
где 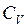 – молярная теплоемкость газа при постоянном объеме.
– молярная теплоемкость газа при постоянном объеме.
Связь между молярной и удельной теплоемкостями
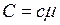 , (II.29)
, (II.29)
где 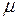 - молярная масса.
- молярная масса.
Теплоемкость газа при постоянном объеме

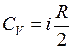 , (II.30)
, (II.30)
где 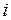 – число степеней свободы движения молекулы.
– число степеней свободы движения молекулы.
Теплоемкость газа при постоянном давлении (уравнение Майера)
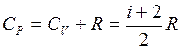 . (II.31)
. (II.31)
Работа при изотермическом процессе
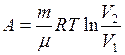 . (II.32)
. (II.32)
Работа при изобарическом процессе
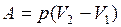 . (II.33)
. (II.33)
Работа при адиабатическом процессе
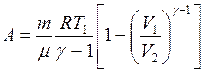 , (II.34)
, (II.34)
где 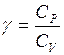 − показатель адиабаты.
− показатель адиабаты.
Уравнения Пуассона
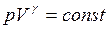 ;
; 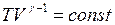 ;
; 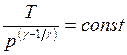 . (II.35)
. (II.35)
ЗАДАЧА № II.60Можно ли говорить о количестветепла,содержащемся в теле?
Ответ: нельзя, так как количество тепла не является функцией состояния системы, а характеризует процесс теплопередачи и зависит от способа теплопередачи.
ЗАДАЧА № II.61Почему наличие большого водоема смягчает климат?
Ответ: Водоем обладает большой теплоемкостью. При похолодании, когда температура воздуха меньше температуры воды, вода отдает большее количества тепла. При потеплении, когда температура воздуха выше температуры воды, вода поглощает много тепла. Этим объясняется сглаживание температурных контрастов.
ЗАДАЧА № II.62 Почему при холостых выстрелах ствол пушки нагревается сильнее, чем при стрельбе снарядами?
Ответ: Энергия, выделяемая при сгорании пороха, в случае холостого выстрела вся идет на нагревание ствола, а при стрельбе снарядами часть энергии идет на придание кинетической энергии снаряду и отдачи.
ЗАДАЧА № II.63Послесильногоштормаводавморе становится теплее. Почему?
Ответ: Нагревание воды происходит за счет превращения механической энергии волн при трении одних слоев о другие в тепло.
ЗАДАЧА № II.64Нагретый сжатый идеальный газ с силой вырывается через два одинаковых сопла наружу. Одна из струй попадает на лопасти турбины, приводя ее во вращение. В какой струе газ охлаждается сильнее? Почему?
Ответ: В струе, падающей на лопасти турбины, т.к. часть тепла расходуется на работу турбины.
ЗАДАЧА № II.65Идеальный газ совершает цикл, состоящий из двух изотерм и двух изохор (рис.30). Как ведут себя на каждом участке:
 Рисунок 30- Заданный цикл
Рисунок 30- Заданный цикл
| а) внутренняя энергия;
б) работа газа;
в) количество теплоты?
Ответ: Для осуществления цикла 1-2-3-4-1 необходим контакт с нагревателем на участках 1-2 и 4-1 и контакт с холодильником на участках 2-3 и 3-4. При анализе поведения внутренней энергии U, работы газа А, количества теплоты Q на каждом участке используем первое начало термодинамики  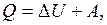
|
выражение внутренней энергии идеального газа 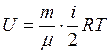 , работу газа
, работу газа  , условия
, условия 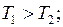 .
. 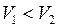
В результате получим:
(1–2) – изотермическое расширение при температуре 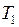 ,
, 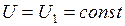 ,
,
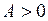 (газ совершает работу путем расширения),
(газ совершает работу путем расширения), 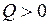 (газ получает тепло от нагревателя);
(газ получает тепло от нагревателя);
(2–3) – изохорический процесс с понижением температуры от T1 до T2 , 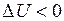 (внутренняя энергия убывает),
(внутренняя энергия убывает), 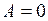 , так как
, так как 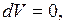
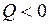 (газ отдает тепло охладителю);
(газ отдает тепло охладителю);
(3–4) – изотермическое сжатие при температуре 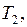
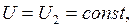
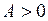 (работа совершается внешними силами над газом),
(работа совершается внешними силами над газом), 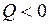 (газ отдает тепло охладителю);
(газ отдает тепло охладителю);
(4–1) – изохорический процесс с повышением температуры от 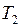 до
до 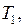
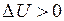 (внутренняя энергия растет)
(внутренняя энергия растет) 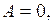
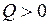 (газ получает тепло).
(газ получает тепло).
ЗАДАЧА № II.66Идеальныйгазрасширяетсяотобъема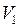 до объема
до объема 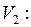
а)адиабатически; б)изобарически; в)изотермически. При каком процессе произведена наименьшая работа?

Рисунок 31 – Графики процессов
Ответ: При адиабатическом процессе (рис.31).
Работа равна 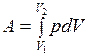 и численно может быть найдена по площади криволинейной трапеции, ограниченной графиком процесса, ординатами начального и конечного состояний и абсциссой.
и численно может быть найдена по площади криволинейной трапеции, ограниченной графиком процесса, ординатами начального и конечного состояний и абсциссой.
ЗАДАЧА № II.67Как меняется температура идеального газа (увеличивается или уменьшается) в процессе, график которого в координатах 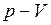 дан на рис. 32.
дан на рис. 32.
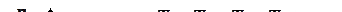

Рисунок 32 – Заданный процесс Рисунок 33 – Серия изотерм
Ответ: Для установления изменения температуры проведём серию изотерм (рис.33). Из рисунка видно, что на участке ( 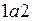 )
) 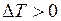 - газ нагревается; на участке (
- газ нагревается; на участке ( 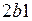 )
) 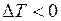 - газ охлаждается.
- газ охлаждается.
ЗАДАЧА № II.68 Увеличится или уменьшится внутренняя энергия идеального газа, если определенное количество газа перевели из состояния 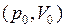 в состояние
в состояние 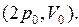 Начальное состояние идеального газа определяется значениями параметров:
Начальное состояние идеального газа определяется значениями параметров: 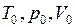 . Конечное состояние идеального газа определяют параметры:
. Конечное состояние идеального газа определяют параметры: 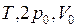 .
.
Ответ:Для двух состояний 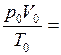
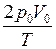 , отсюда,
, отсюда, 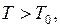 следовательно,
следовательно, 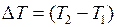 увеличится и
увеличится и 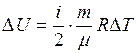 также возрастет.
также возрастет.
ЗАДАЧА №II.69 Два различных газа, из которых один одноатомный, а другой двухатомный, находятся при одинаковых температурах и занимают одинаковые объемы. Газы сжимаются адиабатически так, что их объемы уменьшаются в два раза. Какой из газов нагревается больше?
Ответ: Одноатомный газ нагревается больше. Для сравнения найдем значения показателя Пуассона для одноатомного газа
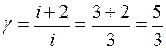 , для двухатомного газа
, для двухатомного газа 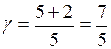 . Используя уравнение адиабаты
. Используя уравнение адиабаты 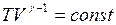 , получим
, получим 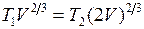 и
и 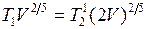 , откуда получим
, откуда получим 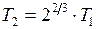 и
и 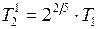 . Следовательно,
. Следовательно, 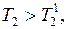 так как
так как 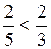 , одноатомный газ нагревается больше.
, одноатомный газ нагревается больше.
ЗАДАЧА № II.70Найти показатель адиабаты 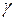 для смеси 1 кг водорода и 2 кг гелия.
для смеси 1 кг водорода и 2 кг гелия.
Дано: 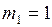 кг;
кг; 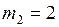 кг;
кг;
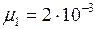 кг/моль;
кг/моль;
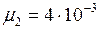 кг/моль.
кг/моль.
Найти: 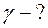
Решение
Найдем показатель адиабаты как отношение 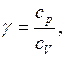
где 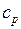 – удельная теплоемкость смеси газов при
– удельная теплоемкость смеси газов при 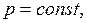
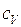 – удельная теплоемкость смеси газов при
– удельная теплоемкость смеси газов при 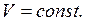
Для нахождения 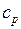 и
и 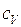 применим формулу для расчета количества теплоты при нагревании смеси
применим формулу для расчета количества теплоты при нагревании смеси

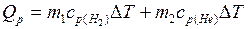 при
при 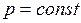 ;
;
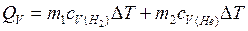 при
при 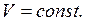
Из определения удельной теплоемкости следует
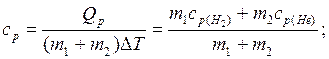
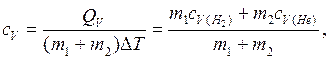
откуда получаем
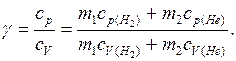
найдем значения удельных теплоемкостей, учитывая, что число степеней свободы 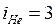 (газ одноатомный),
(газ одноатомный), 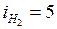 (газ двухатомный), то есть
(газ двухатомный), то есть
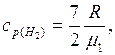
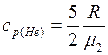 ,
, 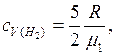
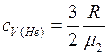 .
.
Подстановка дает
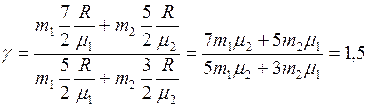
ЗАДАЧА № II.71 6,5 г водорода, находящегося при температуре 27° С, расширяется вдвое при 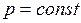 за счет притока тепла извне. Найти: 1) работу расширения; 2)изменение внутренней энергии; 3) количество теплоты, сообщенное газу.
за счет притока тепла извне. Найти: 1) работу расширения; 2)изменение внутренней энергии; 3) количество теплоты, сообщенное газу.
Дано: 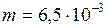 кг;
кг;
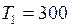 К;
К;
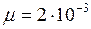 кг/моль;
кг/моль;
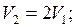
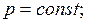
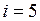
Найти: 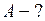
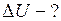
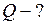
Решение
Приступая к решению задачи, прежде всего надо выявить характер процесса, протекающего в газе, и использовать соответствующие формулы табл.А1. (Приложение) Применение первого начала термодинамики к изопроцессам в идеальных газах
1.Вычислим значения молярных теплоемкостей водорода, учитывая, что молекулы водорода двухатомные и число степеней свободы 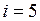

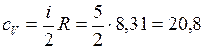 Дж/(моль· К),
Дж/(моль· К),
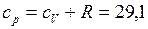 Дж/(моль∙К)
Дж/(моль∙К)
2. Используя условие задачи и уравнение для изобарического процесса 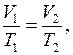 найдем температуру газа после расширения
найдем температуру газа после расширения
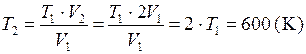 .
.
3. Вычислим изменение внутренней энергии и количество теплоты
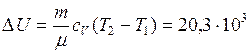 Дж,
Дж,
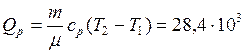 Дж.
Дж.
4. На основании первого начала термодинамики найдем работу расширения газа
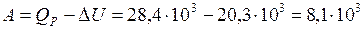 (Дж).
(Дж).
ЗАДАЧА № II.72 Двухатомный идеальный газ, занимающий при давлении 3×105 Па объем 4 л, расширяется до объема 6 л, при этом давление падает до значения 105 Па. Процесс происходит сначала по адиабате (1−x), затем по изохоре (x−2), рис. 34. Определить работу сил давления газа, изменение его внутренней энергии и количество поглощенной теплоты при этом переходе.
Дано: 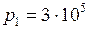 Па;
Па;
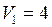 л
л 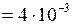 м3 ;
м3 ;
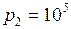 Па
Па
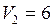 л
л 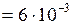 м3 .
м3 .
Найти: 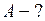
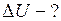
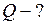

Рисунок 34 - График процессов 1−х−2
Решение
1. Газ участвует в двух процессах: а) адиабатное расширение из состояния 1 в некоторое состояние x, в котором объем
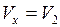 , (1)
, (1)
давление 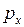 не известно; б) изохорный процесс из состояния x в состояние 2. Найдем
не известно; б) изохорный процесс из состояния x в состояние 2. Найдем 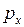 из уравнения адиабаты для двух состояний
из уравнения адиабаты для двух состояний
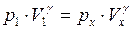
|
Для двухатомного газа 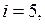 следовательно
следовательно
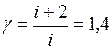 . (3)
. (3)
Значение рх получим на основании (1), (2) и (3), а именно
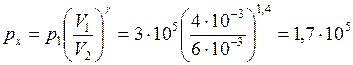 Па.
Па.
Откуда видим, что 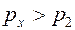 , и процесс 1−2 можно представить графически (рис. 34).
, и процесс 1−2 можно представить графически (рис. 34).
Учтем, что 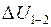 не зависит от вида процесса, а зависит только от начального и конечного состояний газа. Следовательно,
не зависит от вида процесса, а зависит только от начального и конечного состояний газа. Следовательно,
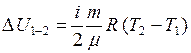 .
.
Из уравнения Клапейрона − Менделеева для состояний 1 и 2 имеем
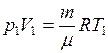 и
и 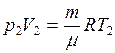 ,
,
откуда получим
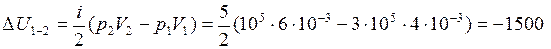 (Дж),
(Дж),
а это значит, что газ охлаждается.
2. Работу 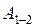 найдем как сумму работ:
найдем как сумму работ: 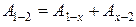 , где для изохоры
, где для изохоры
(х-2) 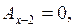 для адиабаты
для адиабаты 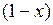
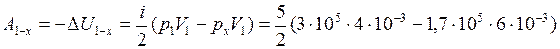 , так как
, так как 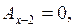 то
то 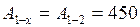 Дж.
Дж.
3. Количество теплоты 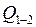 определяется как сумма теплот:
определяется как сумма теплот: 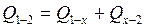 , где (табл.1 А) для адиабаты
, где (табл.1 А) для адиабаты 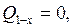 для изохоры
для изохоры 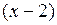
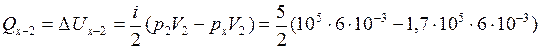 , так как
, так как 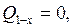 то
то 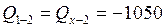 Дж , т.е. газ отдает тепло.
Дж , т.е. газ отдает тепло.
ЗАДАЧА № II.73При изобарическом расширении некоторой массы двухатомного газа, находящегося под давлением 105Па, его внутренняя энергия изменилась на 490 Дж. Найти приращение объема газа.
Дано: 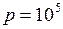 Па;
Па;
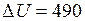 Дж;
Дж;
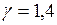
Найти: 
Решение
Чтобы определить приращение объема 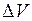 при изобарическом расширении, нужно знать работу, произведенную газом при этом процессе:
при изобарическом расширении, нужно знать работу, произведенную газом при этом процессе: 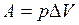 .
.
Работу можно вычислить и на основании первого начала термодинамики: 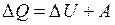 , откуда следует, что
, откуда следует, что 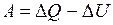 .
.
Количество тепла DQ, сообщенное при изобарическом расширении произвольной массе газа, равно 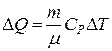 .
.
Изменение внутренней энергии DU, которое произойдет при этом: 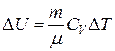 .
.
Разделив 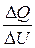 , получим
, получим 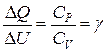 ,
, 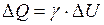 .
.
Подставим это значение в уравнение для работы:
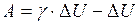 , или
, или 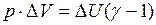 . Найдем из последнего уравнения
. Найдем из последнего уравнения 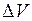
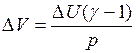 ;
; 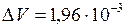 м3.
м3.
ЗАДАЧА № II.74Воздух в комнате объёмом 90 м3 нагревается на 10 К. Какой объём горячей воды должен пройти через радиаторы водяного отопления? Вода охлаждается на 20 К. Потери тепла составляют 50%.
Дано: 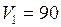 м3;
м3; 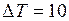 К;
К; 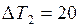 К;
К;
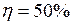 ;
; 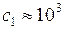 Дж/(кг∙К);
Дж/(кг∙К); 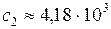 Дж/(кг∙К);
Дж/(кг∙К);
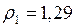 кг/м3;
кг/м3; 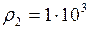 кг/м3.
кг/м3.
Найти: 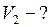
Решение
Количество теплоты, получаемое воздухом 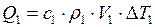 .
.
Количество теплоты, отдаваемое водой 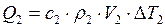 . Учитывая потери энергии, запишем
. Учитывая потери энергии, запишем 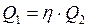 , или
, или 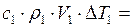
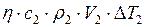 .
.
Отсюда
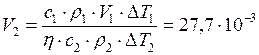 м3.
м3.
ЗАДАЧА № II.75Идеальный газ расширяется изотермически от объёма 0,100 м3 до объёма 0,300 м3. Конечное давление газа 2,00·10 5Па. Определить: а) приращение внутренней энергии газа , б) совершённую газом работу; в) количество полученной газом теплоты.
Дано: 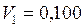 м3;
м3;
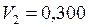 м3;
м3;
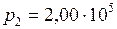 Па.
Па.
Найти: 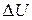 − ? А − ? Q − ?
− ? А − ? Q − ?
Решение
Внутренняя энергия идеального газа пропорциональна термодинамической температуре. Температура газа не изменяется, поэтому 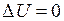 .
.
Работа, совершаемая идеальным газом при изотермическом процессе, определяется формулой: 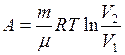 . Согласно уравнению состояния множитель перед логарифмом равен произведению давления на объём. Поэтому можно написать, что
. Согласно уравнению состояния множитель перед логарифмом равен произведению давления на объём. Поэтому можно написать, что 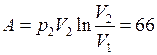 кДж.
кДж.
В соответствии с первым началом термодинамики 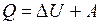 . Следовательно,
. Следовательно, 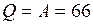 кДж.
кДж.
ЗАДАЧА № II.76Азот, занимающий при давлении 10 5 Па объём 10 л, расширяется вдвое. Найти конечное давление и работу, совершённую газом при следующих процессах: а) изобарном; б) изотермическом; в) адиабатном (рис. 35).
Дано: 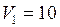 л
л 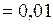 м3;
м3;
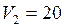 л
л 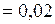 м3;
м3;
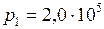 Па.
Па.
Найти: 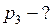
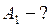
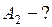
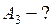

|
Решение:
Из графиков указанных процессов (рис.35) видно, что наибольшая работа при рассматриваемых условиях соответствует изобарному расширению.
Работа при изобарном процессе
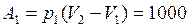 Дж.
Дж.
При изотермическом процессе конечное давление: 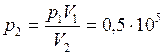 Па.
Па.
Работа газа: 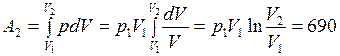 Дж.
Дж.
При адиабатном процессе конечное давление 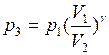 .
.
Азот – двухатомный газ, поэтому 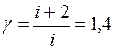 , тогда
, тогда 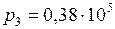 Па.
Па.
Работа, совершаемая газом при адиабатном расширении, равна убыли внутренней энергии
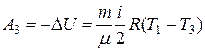 .
.
Из уравнения Клапейрона – Менделеева, написанного для начального и конечного состояний, получаем 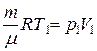 ,
, 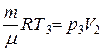 .
.
Подставляя эти выражения в формулу для работы, находим:
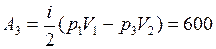 Дж.
Дж.
§II.2.2 ВТОРОЙ ЗАКОН ТЕРМОДИНАМИКИ
Коэффициент полезного действия тепловой машины
Дата добавления: 2016-09-06; просмотров: 2959;











