II.1.3 СТАТИСТИЧЕСКАЯ ФИЗИКА
Число молекул, относительные скорости которых заключены в данном интервале (распределение Максвелла)
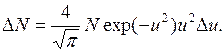 (II.10)
(II.10)
Относительная скорость молекул
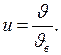 (II.11)
(II.11)
Формула изменения концентрации молекул с высотой
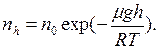 (II.12)
(II.12)
Барометрическая формула
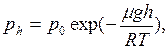 (II.13)
(II.13)
где 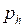 и
и 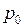 – давление,
– давление, 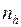 и
и 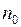 – концентрация газа на высоте
– концентрация газа на высоте 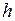 и
и 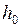 ;
;
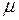 - молярная масса газа;
- молярная масса газа; 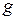 – ускорение свободного падения.
– ускорение свободного падения.
Средняя квадратичная скорость молекул
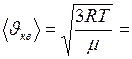
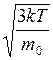 .(II.14)
.(II.14)
Средняя арифметическая скорость молекул
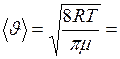
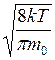 .(II.15)
.(II.15)
Наиболее вероятная скорость
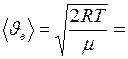
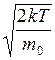 ,(II.16)
,(II.16)
где 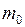 – масса одной молекулы.
– масса одной молекулы.
ЗАДАЧА № II.33В законе распределения Максвелла для газовых молекул по скоростям кривая распределения асимптотически приближается к оси скоростей. Означает ли это, что молекулы газа, пусть с малой вероятностью, но могут иметь сколь угодно большие скорости?
Ответ: Скорость молекул ограничена определенным значением энергии теплового движения газа при данной температуре.
ЗАДАЧА № II.34 Возможны ли в газе с температурой 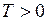 К неподвижные молекулы?
К неподвижные молекулы?
Ответ: Их вероятность исчезающее мала, т.к. кривая распределения Максвелла проходит через начало координат.
ЗАДАЧА № II. 35Какой вид приобретет барометрическая формула на большой высоте?
Ответ:С высотой ускорение свободного падения уменьшается, поэтому необходимо использовать потенциальную энергию гравитационного поля
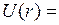
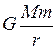 , и барометрическая формула примет вид
, и барометрическая формула примет вид 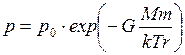 , где
, где 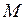 – масса Земли,
– масса Земли, 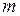 – масса молекулы газа.
– масса молекулы газа.
ЗАДАЧА № II.36Как можно трактовать нормировку функции распределения Максвелла, а именно 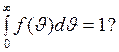
Ответ:Как достоверное событие, имеющее вероятность равную единице.
ЗАДАЧА №II.37Почему отличаются по своему значению средняя квадратичная, средняя арифметическая и наиболее вероятная скорости газовых молекул?
Ответ:Это вызвано асимметричностью кривой распределения Максвелла.
ЗАДАЧА№ II.38Почему с повышением температуры газа вместе с расширением кривой распределения понижается ее максимум?
Ответ: Это следует из условия нормировки, а следовательно из постоянства площади под кривой.
ЗАДАЧА № II.39Влияют ли на максвелловское распределение молекул по скоростям параметры состояния газа?
Ответ:Влияет только температура.
ЗАДАЧА № II.40Если число молекул в сосуде увеличили, не изменив температуры, то как изменится число молекул, обладающих наиболее вероятной скоростью в максвелловском распределении молекул по скоростям?
Ответ: Число молекул, обладающих наиболее вероятными скоростями, увеличится.
ЗАДАЧА № II.41 В трех одинаковых сосудах при равных условиях находится одинаковое количество азота (N2), гелия (He), и водорода (H2). На рис. 27 дано распределение скоростей этих молекул. Каким кривым распределения соответствуют молекулы водорода и азота?
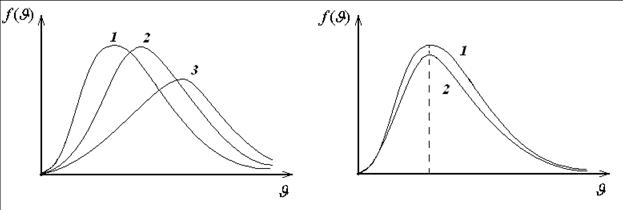
Рисунок 27- Распределение скоростей Рисунок 28- Кривые 1 и 2
молекул
Ответ: Водороду – 3, азоту – 1. Наиболее вероятная скорость 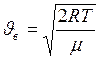 , она зависит от молярной массы газа и будет наименьшей для азота, (
, она зависит от молярной массы газа и будет наименьшей для азота, ( 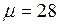 г/моль) и наибольшей у водорода (
г/моль) и наибольшей у водорода ( 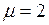 г/моль).
г/моль).
ЗАДАЧА № II.42 В сосуде, разделенном на равные части неподвижной непроницаемой перегородкой, находится газ. Температуры газа в каждой части сосуда равны, масса газа в левой части больше, чем в правой 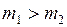 . Какими кривыми (рис.28) будут описываться функции распределения молекул по скоростям для молекул газа в правой и левой частях сосуда?
. Какими кривыми (рис.28) будут описываться функции распределения молекул по скоростям для молекул газа в правой и левой частях сосуда?
Ответ: Газ в обеих частях сосуда одинаковый, температуры равны, следовательно наиболее вероятные скорости молекул тоже равны 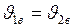 . Массы разные
. Массы разные 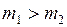 . В большей массе будет большее число молекул, следовательно, будет больше площадь под кривой функции распределения
. В большей массе будет большее число молекул, следовательно, будет больше площадь под кривой функции распределения
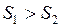 . Кривая 1 – для левой части, кривая 2 – для правой части.
. Кривая 1 – для левой части, кривая 2 – для правой части.
ЗАДАЧА № II.43 Определить долю молекул водорода, модули скоростей которых при температуре 27° С лежат в интервале от 1898 м/с до 1902 м/с.
Дано: 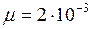 кг/моль;
кг/моль;
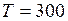 К;
К;
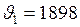 м/с;
м/с;
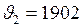 м/с.
м/с.
Найти: 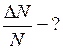
Решение
В данной задаче удобнее воспользоваться распределением молекул по относительным скоростям. Доля молекул 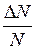 , относительные скорости которых заключены в интервале от
, относительные скорости которых заключены в интервале от 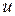 до
до 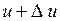 , определяется формулой
, определяется формулой
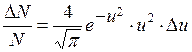 , (1)
, (1)
где 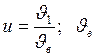 – наиболее вероятная скорость;
– наиболее вероятная скорость; 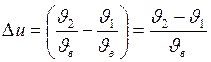 .
.
С учетом этих выражений формула (1) примет вид
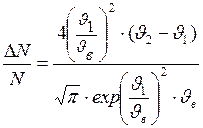 .
.
Для удобства сначала вычислим 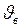
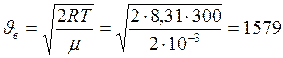 (м/с),
(м/с),
и отношение скоростей 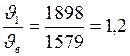 .
.
Подставим численные значения в (1) и найдем долю молекул водорода, модули скоростей которых лежат в интервале от 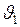 до
до 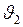
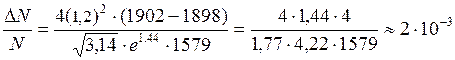 .
.
ЗАДАЧА № II.44Броуновские частицы с массой 4 фгведут себя в тепловом движении подобно гигантским молекулам, и к ним можно применить закономерности молекулярно-кинетической теории. Исходя из этого, определить, во сколько раз уменьшится концентрация броуновских частиц при увеличении высоты на 1 мм. Температуру принять равной 300 К.
Дано: 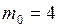 фг
фг 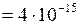 г
г 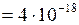 кг;
кг;
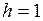 мм
мм 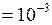 м;
м;
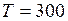 К.
К.
Найти: 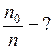
Решение
Для броуновских частиц воспользуемся распределением молекул по
высоте (распределение Больцмана)
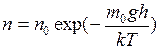 ,
,
где 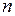 и
и 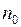 – концентрация молекул на высоте
– концентрация молекул на высоте 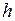 и на высоте
и на высоте 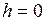 , соответственно. Выразим
, соответственно. Выразим
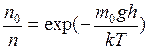
Прологарифмируем и подставим численные значения,
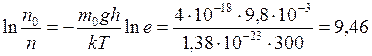 .
.
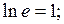
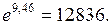 Итак,
Итак, 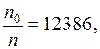 то есть концентрация частиц уменьшится в
то есть концентрация частиц уменьшится в 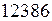 раз.
раз.
ЗАДАЧА № II.45 На какой высоте над уровнем моря атмосферное давление составляет 78 кПа, если температура воздуха 170С и не меняется с высотой, а давление на уровне моря нормальное? Найти число частиц в единице объема на этой высоте.
Дано: 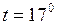 C
C 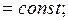
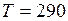 К;
К;
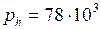 Па;
Па;
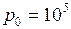 Па;
Па;
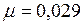 кг/моль.
кг/моль.
Найти: 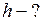
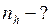
Решение
Если температура не меняется с высотой, то для нахождения давления можно воспользоваться барометрической формулой (II.13)
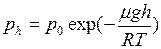
логарифмируя эту формулу, получаем
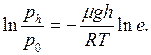
Отсюда находим 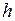
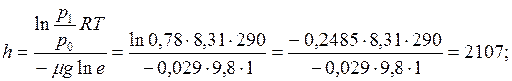
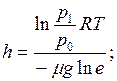

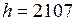 м;
м; 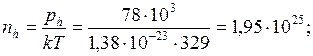
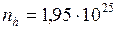 м-3.
м-3.
ЗАДАЧА № II.46Найти число молекул водорода, заключенных в 1см3 при нормальных условиях, а также число молекул значения скоростей которых лежат в интервале между 399 и 401 м/с.
Дано: 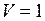 см3
см3 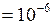 м3;
м3;
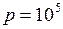 Па;
Па;
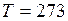 К;
К;
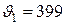 м/с;
м/с;
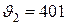 м/с;
м/с;
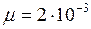 кг/моль;
кг/моль;
Найти: 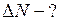
Решение
Число молекул можно найти из распределения Максвелла, заданного в виде уравнения (II.10)
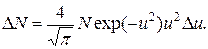
Для всех газов при нормальных условиях число молекул в 1 см3 одно и то же и равно 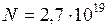 см-3 (число Лошмидта).
см-3 (число Лошмидта).
Вычислим значения величин, входящих в распределение Максвелла
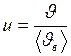 ,
, 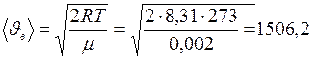 м/с;
м/с;
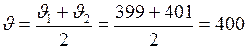 м/с;
м/с; 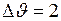 м/с;
м/с;
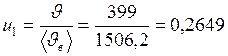
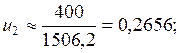
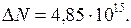
ЗАДАЧА № II.47Температура окиси азота (NO) 300 К. Определить долю молекул, скорость которых лежит в интервале от 820 м/с до 830 м/с.
Дано: 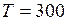 К;
К;
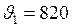 м/с;
м/с;
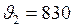 м/с;
м/с;
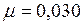 кг/моль.
кг/моль.
Найти: 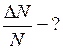
Решение
Рассматриваемый газ находится в равновесном состоянии. Согласно распределению Максвелла, относительное число молекул, скорость которых заключена в интервале от 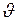 до
до 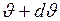 ,
, 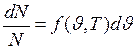 ,
,
где 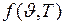 – функция распределения Максвелла, которую можно представить в виде:
– функция распределения Максвелла, которую можно представить в виде: 
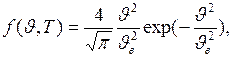 где
где 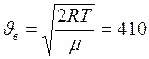 м/с.
м/с.
Тогда
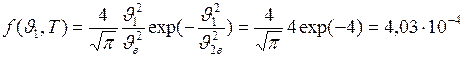 с/м.
с/м.
Аналогично подсчитаем 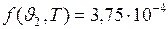 с/м.
с/м.
В условии задачи требуется определить долю молекул, скорости которых лежат в диапазоне 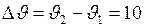 м/с.
м/с.
Если в этом пределе функцию Максвелла можно с достаточной степенью точности считать постоянной, то искомая величина может быть рассчитана по приближённой формуле
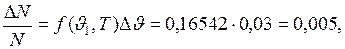 т.е.
т.е. 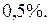 Это значит, что при использовании этой формулы допускается ошибка, относительная величина которой
Это значит, что при использовании этой формулы допускается ошибка, относительная величина которой
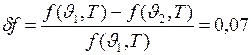 .
.
Следовательно, с указанной степенью точности можно использовать равенство 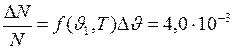 , или
, или 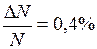 .
.
Дата добавления: 2016-09-06; просмотров: 4771;











