Для идеального газа
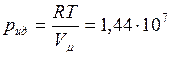 Па.
Па.
Таким образом, 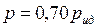 .
.
ЗАДАЧА № II.105Моль кислорода расширяется адиабатически в пустоту, в результате чего объём газа увеличивается от 1 л до 10 л. Определить приращение температуры газа.
Дано: 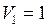 л
л 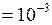 м3;
м3;
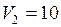 л
л 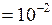 м3;
м3;
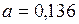 (Па·м6)/(моль2).
(Па·м6)/(моль2).
Найти: 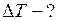
Решение
Расширяясь в пустоту, газ работы не совершает 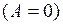 . При адиабатическом процессе
. При адиабатическом процессе 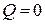 . Поэтому согласно первому началу термодинамики
. Поэтому согласно первому началу термодинамики 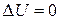 . Внутренняя энергия моля ван – дер– ваальсовского газа с двухатомными жёсткими молекулами определяется выражением
. Внутренняя энергия моля ван – дер– ваальсовского газа с двухатомными жёсткими молекулами определяется выражением
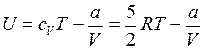 .
.
Приравняв значения этого выражения для начального и конечного состояний газа, получим, что
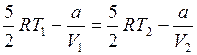 , откуда
, откуда 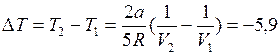 К.
К.
Газ охладился на 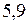 К.
К.
§II.2.4 ЖИДКОСТИ
Поверхностное натяжение жидкости
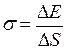 , (II.45)
, (II.45)
где 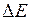 – изменение свободной энергии поверхностного слоя жидкости;
– изменение свободной энергии поверхностного слоя жидкости;
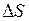 – изменение площади этого слоя.
– изменение площади этого слоя.
Добавочное давление, вызванное кривизной поверхности жидкости (формула Лапласа)
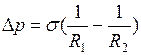 , (II.46)
, (II.46)
где 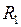 и
и 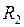 – радиусы кривизны двух взаимно перпендикулярных сечений поверхности жидкости.
– радиусы кривизны двух взаимно перпендикулярных сечений поверхности жидкости.
Высота поднятия жидкости в капиллярных трубках
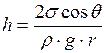 , (II.47)
, (II.47)
где 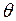 − краевой угол;
− краевой угол;
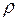 − плотность жидкости;
− плотность жидкости;
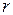 – радиус канала трубки.
– радиус канала трубки.
Работа при изотермическом увеличении поверхности жидкости
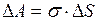 . (II.48)
. (II.48)
Сила сцепления между пластинками, смачиваемыми жидкостью, расположенными на расстоянии 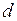
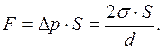 (II.49)
(II.49)
Относительное изменение объема жидкости при нагревании
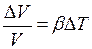 , (II.50)
, (II.50)
где 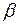 − температурный коэффициент объемного расширения.
− температурный коэффициент объемного расширения.
Относительное изменение объема жидкости при изменении давления
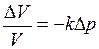 , (II.51)
, (II.51)
где 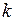 – коэффициент сжатия.
– коэффициент сжатия.
Плотность жидкости при температуре 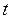
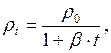 (II.52)
(II.52)
где 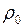 – плотность при
– плотность при 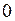 0С.
0С.
Осмотическое давление раствора (формула Вант – Гоффа)
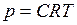 , (II.53)
, (II.53)
где 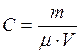 − число молей растворенного вещества в единице объема раствора.
− число молей растворенного вещества в единице объема раствора.
ЗАДАЧА № II.106Нефть,разлитая на поверхности воды, создает радужные полосы. Каково их происхождение?
Ответ:Нефть полностью смачивается водой и под действием сил поверхностного натяжения растекается до очень тонкой пленки (в пределе до мономолекулярного слоя), в которой в результате интерференции падающего на поверхность пленки света и возникает радужная картина.
ЗАДАЧА № II.107По правилам техники безопасности, рассыпавшуюся на шарики ртуть собирают медным совочком и медной щеточкой. Почему?
Ответ: Ртуть рассыпается на шарообразные капельки, т.к. не смачивает большинство поверхностей и к ним не прилипает. Медь же полностью смачивается ртутью и ее легко удается собрать.
ЗАДАЧА № II.108Почему при касании с водой легко намокают пористые предметы?
Ответ:Поры – это капилляры и действует капиллярный эффект.
ЗАДАЧА № II.109Почему на поверхности возникают поперечные волны, тогда как известно, что для образования поперечных волн среда должна обладать упругостью сдвига, чего нет в жидкости.
Ответ: Упругость сдвига на поверхности жидкости создают силы поверхностного натяжения.
ЗАДАЧА № II.110Почему можно использовать ртутные термометры для измерения температур до + 500 0 С , если ртуть кипит при температуре
+ 367 0 С?
Ответ: При изготовлении термометров, способных измерять температуру до + 550 0 С, в пространстве над ртутью вводят азот под давлением 14 атмосфер, вследствие чего температура кипения ртути соответственно повышается.
ЗАДАЧА № II.111За высоко летящим самолетом иногда образуется шлейф. Как объяснить его происхождение?
Ответ: Выбрасываемые частицы сгоревшего топлива являются центрами конденсации пересыщенного пара. Пар конденсируется и за самолетом образуется облачный след.
ЗАДАЧА № II.112На раскаленную плиту попадает капля воды, образуя приплюснутый шарик, который спокойно, почти не испаряясь, лежит на раскаленном металле. Стоит прекратить нагрев электроплитки, водяной шарик мгновенно испарится. Как объяснить это явление?
Ответ: Под водяной каплей образуется «паровая подушка», которая плохо проводит тепло. Поэтому, капля лежит на раскаленном металле почти не испаряясь. При уменьшении температуры плиты паровая опора исчезает, капля касается металла и мгновенно испаряется.
ЗАДАЧА № II.113Чайник перед закипанием в нем воды «поет». Как объяснить это явление?
Ответ: Пузырьки конденсированного в воде воздуха поднимаются к ее поверхности, лопаются, создавая звуковые колебания воздуха.
ЗАДАЧА № II.114 На асфальте морозной зимой образуются выпуклости, на бетонных дорогах – трещины, а иногда за зиму дорогу сильно «вспучивает». Высота вспучиваний достигает порой 20–30 см. Что вызывает эти явления?
Ответ: Расширениемзамерзающей под асфальтом воды нельзя объяснить столь значительное вспучивание. Оно усиливается вследствие замерзания воды, которая поднимается из нижних слоев почвы вверх.
ЗАДАЧА № II.115Имеется прибор, состоящий из двух стеклянных шариков, соединенных трубкой (рис.39). Шарики частично заполнены спиртом, а воздух откачен. Прибор укреплен на оси под кюветой, заполненной водой, в которую шарики поочередно опускаются, совершая колебательное движение. Чем это обьяснить?
Ответ: Шарик, в котором оказалось больше спирта, перевешивает, и соприкасаясь с теплой водой, нагревается, в этом шарика возрастает давление насыщенных паров спирта, занимающих пространство над жидким спиртом. Поэтому спирт из нижнего шарика вытесняется в верхний, в котором давление насыщенных паров будет меньше. Последний перевешивается и погружается в воду. Через некоторое время процесс повторяется.
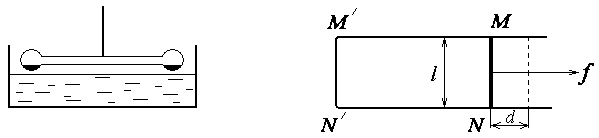
Рисунок 39 - Прибор со стеклянными Рисунок 40 -Проволочная рамка
шариками
ЗАДАЧА № II.116На вынутой из мыльного раствора проволочной рамке образуется мыльная пленка (рис. 40 ). Одна из проволок MN рамки может скользить вдоль проволок ММ и NN . Длина подвижной проволочки l равна 5 мм. Зависимость поверхностного натяжения 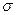 воды от температуры дается формулой
воды от температуры дается формулой 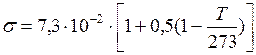 . Найти при изотермическом процессе для
. Найти при изотермическом процессе для 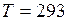 К силу
К силу 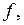 работу
работу 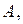 которая затрачивается при растяжении пленки на
которая затрачивается при растяжении пленки на 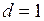 см и изменение внутренней энергии системы
см и изменение внутренней энергии системы 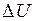 при увеличении площади пленки на 1 см2 . Чему равна скрытая теплота образования пленки
при увеличении площади пленки на 1 см2 . Чему равна скрытая теплота образования пленки 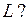 (Примечание
(Примечание 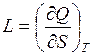 , где
, где 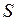 - площадь пленки).
- площадь пленки).
Дано: 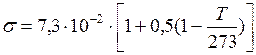 ;
;
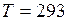 К;
К;
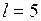 мм
мм 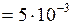 м;
м;
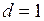 см
см 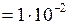 м;
м;
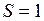 см2
см2 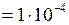 м2.
м2.
Найти: 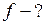
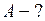
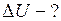
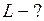
Решение
Запишем баланс энергий 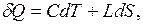 где
где 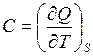 теплоемкость пленки. Первое начало термодинамики примет вид
теплоемкость пленки. Первое начало термодинамики примет вид
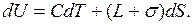
Сила и работа равны соответственно
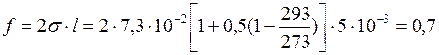 мН,
мН,
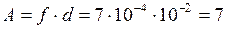 мкДж, где учтено, что пленка имеет две поверхности.
мкДж, где учтено, что пленка имеет две поверхности.
Для энтропии получаем формулу 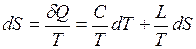 , следовательно
, следовательно
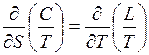 , (1)
, (1)
откуда
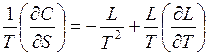 (2)
(2)
С другой стороны, учитывая, что 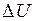 также полный дифференциал, можем написать
также полный дифференциал, можем написать
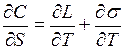 .
.
Из (1) и (2) находим
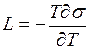 .
.
Принимая во внимание, что 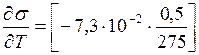 Дж/(м2 ∙ К),
Дж/(м2 ∙ К),
получаем 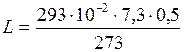
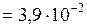 Дж/м2.
Дж/м2.
Поскольку 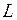 положительно, пленка при увеличении поверхности охлаждается. Изменение внутренней энергии при
положительно, пленка при увеличении поверхности охлаждается. Изменение внутренней энергии при 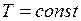 равно
равно
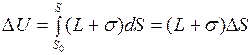 , т.к.
, т.к. 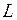 и
и 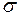 от
от 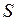 не зависит. Учитывая, что
не зависит. Учитывая, что 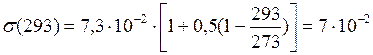 Дж/м2
Дж/м2
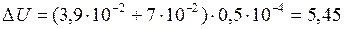 мкДж.
мкДж.
ЗАДАЧА № II.117Внутри пузыря из мыльной воды добавочное давление 0,32 мм.рт.ст. Каков радиус этого пузыря, какую работу надо совершить для выдувания пузыря и какова свободная энергия поверхностной пленки пузыря?
Дано: 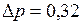 мм.рт.ст.
мм.рт.ст. 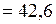 Па;
Па;
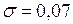 Н/м
Н/м
Найти: 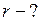
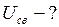
Решение
Давление внутри мыльного пузыря равно атмосферному, сложенному с добавочным лапласовским
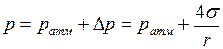 ,
,
откуда
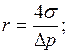
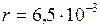 м.
м.
Работа выдувания пузыря равна изменению поверхностной энергии внутренней и внешней сферических поверхностей пленки
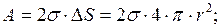
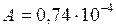 Дж.
Дж.
Свободная энергия равна работе растяжения
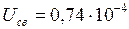 Дж.
Дж.
ЗАДАЧА № II.118Цилиндрическая трубка А (рис. 41) с площадью сечение 1·10-4 м2 содержит раствор сахара (С12Н22О11). Снизу она закрыта полупроницаемой перепонкой С, пропускающей чистую воду, но не пропускающей молекул сахара. Трубка А опущена в сосуд с чистой водой, причем перепонка С находится на глубине 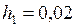 м ниже уровня воды в сосуде В. При равновесии уровень раствора в трубке А на
м ниже уровня воды в сосуде В. При равновесии уровень раствора в трубке А на 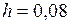 м выше уровня воды в сосуде В. Температура
м выше уровня воды в сосуде В. Температура 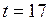 0C, плотность раствора мало отличается от плотности воды. Сколько сахара содержится в трубке А?
0C, плотность раствора мало отличается от плотности воды. Сколько сахара содержится в трубке А?
Дано: 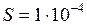 м2;
м2;
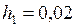 м;
м;
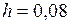 м;
м;
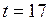 0C;
0C; 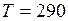 К;
К;
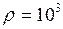 кг/м3 ;
кг/м3 ;
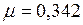 кг/моль;
кг/моль;
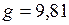 м/c2.
м/c2.
Найти: 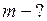
Решение

Уровень жидкости в трубке А поднимается до тех пор, пока гидростатическое давление поднявшегося столба жидкости не окажется равным осмотическому давлению. Гидростатическое давление равно
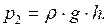
Осмотическое давление можно подсчитать по закону Вант – Гоффа
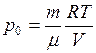 ,
,
где 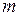 – масса растворенного вещества;
– масса растворенного вещества;
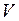 –объем, занимаемый раствором, т.е.
–объем, занимаемый раствором, т.е.
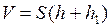 .
.
Запишем условие равновесия
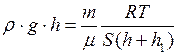 ,
,
откуда
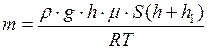 .
.
Вычисляя в системе СИ, получим: 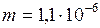 кг.
кг.
ЗАДАЧА № II.119Масса спирта, взятого при 00С в объеме 500 см3, равна 400 г. Определить плотность спирта при 150С.
Дано: 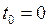 0С;
0С; 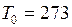 К;
К;
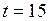 0С;
0С; 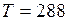 К;
К;
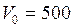 см3
см3 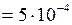 м3;
м3;
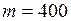 г
г 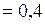 кг;
кг;
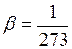 град-1.
град-1.
Найти: 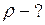
Решение
Определяем плотность спирта по формуле (II.57)

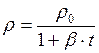 .
.
Поскольку 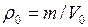 , то формула (2.56) примет вид
, то формула (2.56) примет вид
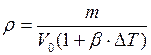 .
.
Учитывая формулу приближенного вычисления, находим
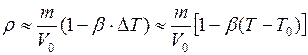 ;
; 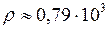 кг/м3
кг/м3
ЗАДАЧА № II.120В стеклянную трубку с внутренним диаметром 20мм вставлена коаксиально стеклянная палочка диаметра 19 мм. Считая смачивание полным, определить высоту капиллярного поднятия воды в кольцевом зазоре между трубкой и палочкой.
Дано: 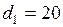 мм
мм 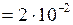 м;
м;
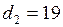 мм
мм 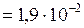 м;
м;
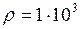 кг/м3
кг/м3
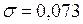 Н/м
Н/м
Найти: 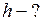
Решение
Так как ширина зазора 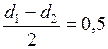 мм в 40 раз меньше диаметра трубки, среднюю кривизну поверхности воды в зазоре можно считать равной
мм в 40 раз меньше диаметра трубки, среднюю кривизну поверхности воды в зазоре можно считать равной 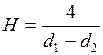 . Подстановка этого значения в формулу Лапласа даёт, что
. Подстановка этого значения в формулу Лапласа даёт, что
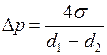 .
.
Капиллярное давление 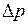 уравновешивается гидростатическим давлением (
уравновешивается гидростатическим давлением ( 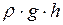 ). Следовательно,
). Следовательно, 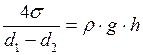 , откуда
, откуда 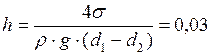 м.
м.
ЗАДАЧА № II.121Рамку в виде равностороннего треугольника со стороной 4 см аккуратно положили на поверхность воды. Какая сила удерживает рамку на воде? Какую силу необходимо приложить, чтобы оторвать рамку от поверхности воды? Масса рамки 2 г.
Дано: 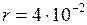 м;
м;
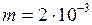 кг;
кг;
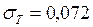 Н/м.
Н/м.
Найти: 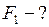
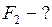
Решение
На поверхности воды рамка удерживается силой поверхностного натяжения 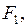 которую можно найти из формулы
которую можно найти из формулы 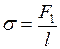 ,
,
где 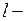 длина внешней и внутренней границы поверхности жидкости, равная удвоенному периметру треугольника
длина внешней и внутренней границы поверхности жидкости, равная удвоенному периметру треугольника 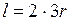 , тогда
, тогда 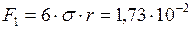 Н.
Н.
Для отрыва рамки от поверхности воды необходимо преодолеть кроме силы поверхностного натяжения ещё силу тяжести рамки, т.е.
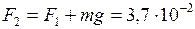 Н.
Н.
ЗАДАЧА № II.122В лабораторной работе по определению поверхностного натяжения воды использовали метод отрыва капель. С помощью бюретки, имеющий диаметр внутреннего отверстия 1,8 мм, отсчитали 100 капель, масса которых оказалась равной 3,78 г. Найти по этим данным поверхностное натяжение воды и, сравнив его с табличным значением, определить относительную погрешность измерений.
Дано: 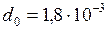 м;
м;
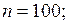
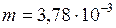 кг;
кг;
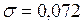 Н/м.
Н/м.
Найти: 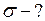
Решение
При не полностью открытом кране вода из бюретки будет вытекать каплями, причём перед отрывом диаметр шейки капли 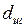 будет меньше диаметра отверстия бюретки
будет меньше диаметра отверстия бюретки 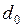 . Обычно это соотношение
. Обычно это соотношение 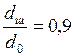 . Капля отрывается, когда сила тяжести её становится равной или чуть больше силы поверхностного натяжения:
. Капля отрывается, когда сила тяжести её становится равной или чуть больше силы поверхностного натяжения: 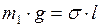 , где
, где 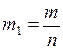 ;
; 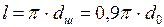 . Следовательно,
. Следовательно, 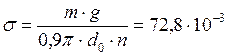 Н/м
Н/м
Абсолютную погрешность 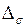 найдём из разности
найдём из разности 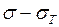
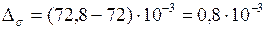 Н/м
Н/м
Относительная погрешность равна отношению абсолютной погрешности к табличному значению поверхностного натяжения
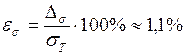 .
.
§II.2.5 ТВЁРДЫЕ ТЕЛА
Относительное изменение длины при изменении температуры на DТ
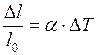 , (II.54)
, (II.54)
где 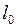 – начальная длина;
– начальная длина;
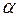 − коэффициент линейного расширения.
− коэффициент линейного расширения.
Относительное изменение объема при изменении температуры на DТ
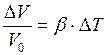 , (II.55)
, (II.55)
где 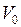 – начальный объем;
– начальный объем;
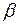 − коэффициент объемного расширения.
− коэффициент объемного расширения.
Для изотропных тел
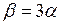 . (II.56)
. (II.56)
Зависимость плотности от температуры
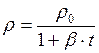 , (II.57)
, (II.57)
где 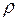 и
и 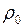 – плотности тела при 0 и
– плотности тела при 0 и 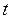 0C
0C
Изменение температуры плавления твердого тела 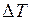 с изменением давления
с изменением давления 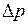 выражается уравнением Клапейрона – Клаузиуса
выражается уравнением Клапейрона – Клаузиуса
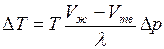 , (II.58)
, (II.58)
где 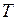 – температура;
– температура;
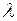 − удельная теплота плавления при нормальных условиях;
− удельная теплота плавления при нормальных условиях;
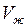 и
и 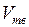 – удельные объемы жидкости и твердого тела.
– удельные объемы жидкости и твердого тела.
Молярная теплоемкость химически простых твердых тел в классической теории теплоемкости (закон Дюлонга – Пти)
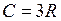 , (II.59)
, (II.59)
где 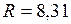 Дж/(моль·К) – постоянная для всех газов величина, называемая молярной газовой постоянной (или универсальной газовой постоянной).
Дж/(моль·К) – постоянная для всех газов величина, называемая молярной газовой постоянной (или универсальной газовой постоянной).
В случае деформации продольного растяжения или одностороннего сжатия стержня относительное изменение длины стержня определяется законом Гука
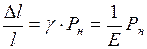 , (II.60)
, (II.60)
где 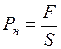 – напряжение;
– напряжение;
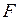 – растягивающая или сжимающая сила;
– растягивающая или сжимающая сила;
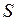 – площадь поперечного сечения;
– площадь поперечного сечения;
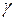 − коэффициент упругости;
− коэффициент упругости;
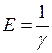 – модуль Юнга.
– модуль Юнга.
Для закручивания стержня круглого сечения длиной 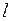 и радиусом
и радиусом 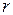 на некоторый угол
на некоторый угол 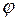 надо приложить крутящий момент (момент пары сил)
надо приложить крутящий момент (момент пары сил)
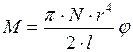 , (II.61)
, (II.61)
где 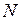 – модуль сдвига материала проволоки.
– модуль сдвига материала проволоки.
Потенциальная энергия 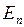 растянутого упругого стержня под влиянием силы
растянутого упругого стержня под влиянием силы 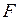 при удлинении
при удлинении 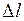 равна
равна
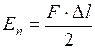 . (II.62)
. (II.62)
При закручивании
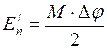 , (II.63)
, (II.63)
где 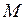 – момент силы, закручивающий стержень на угол
– момент силы, закручивающий стержень на угол 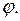
ЗАДАЧА № II.123 Какие свойства красной меди делают ее исключительно удобным материалом для паяльников?
Ответ:У меди большая теплопроводность, благодаря чему медный паяльник быстро отдает большое количество тепла припою. Кроме того, медь
обладает большой удельной теплоемкостью, благодаря чему при нагреве медного паяльника он приобретает большое количество тепла. Другим материалам с этими качествами является серебро.
ЗАДАЧА № II.124 Почему при распиливании дерева циркулярная пила значительно нагревается, а дерево нагревается слабо?
Ответ:Теплоемкость металла много меньше, чем дерева.
ЗАДАЧА № II.125Если резиновую ленту нагреть, она укорачивается. Почему резина ведет себя противоположно металлу?
Ответ: Молекулы резины представляют собой длинные цепи. При нагревании тепловое движение этих цепей усиливается, они сильнее стягиваются, и резина сокращается. Растягивая пружину, т.е. эти молекулярные цепи, вы совершаете работу, которая частично переходит в тепло. Если затем резину отпустить, часть совершаемой упругими силами работы идет на уменьшение внутренней энергии резины, в результате ее температура падает.
ЗАДАЧА № II.126При повышении температуры биметаллическая пластинка должна разомкнуть электрическую цепь (рис. 42). С какой стороны у пластинки медь и где сталь?
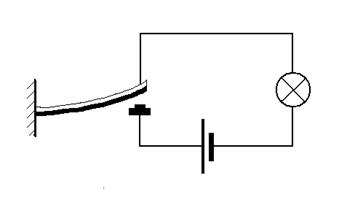
Рисунок 42 - Биметаллическая пластинка.
Ответ:Медь внизу. Имея коэффициент расширения больше, чем у стали, медь расширяется сильнее, и оказывается на внешней части дуги, которую образует биметаллическая пластинка при ее нагревании.
ЗАДАЧА № II.127.С давних пор все повара отдают предпочтение чугунным сковородкам перед стальными. Есть ли этому физическое обоснование?
Ответ: У толстых массивных чугунных сковородок дно прогревается более равномерно, чем у современных, сделанных из тонкой стали. Те участки дна стальных сковородок, которые располагаются непосредственно над огнем, прогреваются особенно сильно, и на них пища пригорает.
ЗАДАЧА № II.128Почему зимой металлические предметы кажутся более холодными чем, например, деревянные или кирпичные, когда вы касаетесь их пальцами?
Ответ:Ощущение холода, которое вызывает у нас тот или иной предмет, зависит не только от его температуры, но и от теплопроводности. Чем быстрее холодный предмет отводит тепло от ваших пальцев, тем более холодным он вам кажется.
ЗАДАЧА № II.129Когда вы измеряете температуру, тепло вашего тела заставляет ртуть в градуснике расширяться. Почему сужение в капилляре градусника не дает упасть столбику ртути после того, как вы измерили температуру. Ведь при расширении ртуть прошла через это сужение. Почему же она не проходит через него, когда сжимается?
Ответ: Диаметр сужения капилляра настолько мал, что ртуть проходит через него только под давлением, которое возникает либо в результате теплового расширения ртути, либо под действием «центробежной » силы (она создается, когда градусник стряхивают, совершая им дугообразные движения). При остывании ртуть в месте сужения разрывается, т.к. молекулярные силы в ртути недостаточно сильны, чтобы втянуть верхнюю часть столбика обратно сквозь сужение капилляра.
ЗАДАЧА № II.130Железная линейка при 150С имеет длину 1м. Насколько изменится длина линейки при охлаждении до (− 350С)?
Дано: 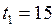 0С;
0С; 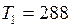 К;
К;
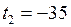 0С;
0С; 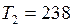 К;
К;
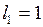 м;
м;
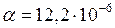 К-1
К-1
Найти: 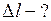
Решение
По закону линейного расширения (II.54)
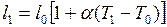 ; (II.64)
; (II.64)
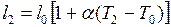 , (II.65)
, (II.65)
где 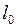 – длина линейки при температуре
– длина линейки при температуре 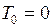 К.
К.
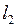 – длина линейки после ее охлаждения до температуры
– длина линейки после ее охлаждения до температуры 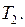
Тогда изменение длины линейки
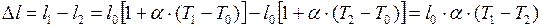 . (II.66)
. (II.66)
Найдя 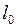 из уравнения (II.64) и подставляя его в выражение (II.66), получаем
из уравнения (II.64) и подставляя его в выражение (II.66), получаем
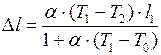 . (II.67)
. (II.67)
Учитывая, что 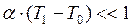 , выражение (II.67) можно приближенно записать в виде
, выражение (II.67) можно приближенно записать в виде
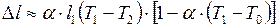 ;
;
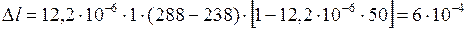 м.
м.
ЗАДАЧА № II.131Используя закон Дюлонга и Пти, определить удельную теплоёмкость меди.
Решение
Согласно закону Дюлонга и Пти моль химически простых веществ в кристаллическом состоянии имеет теплоёмкость 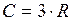 . Удельная теплоёмкость
. Удельная теплоёмкость 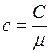 , где
, где 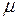 − молярная масса вещества
− молярная масса вещества 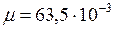 кг/моль. С учётом этих данных
кг/моль. С учётом этих данных 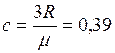 .кДж/(кг∙К)
.кДж/(кг∙К)
ЗАДАЧА № II.132Люстра массой 250 кг подвешена с помощью прутка из алюминия с пределом прочности 0,11 ГПа. Какой должна быть площадь поперечного сечения прутка при запасе прочности 4? Какова относительная деформация прутка?
Дано: 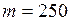 кг;
кг;
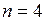 ;
;
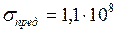 Па;
Па;
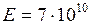 Па.
Па.
Найти: 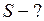
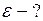
Решение
Деформация прутка вызывается действием силы тяжести люстры 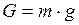 . Площадь поперечного сечения прутка выбирают в зависимости от возникающего в прутке механического напряжения
. Площадь поперечного сечения прутка выбирают в зависимости от возникающего в прутке механического напряжения 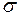
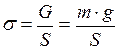 , откуда
, откуда 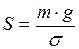 . Зная запас прочности n и предел прочности
. Зная запас прочности n и предел прочности 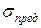 , определим допускаемое напряжение
, определим допускаемое напряжение 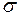 :
: 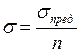 ,
,
где 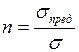 . Окончательно получаем
. Окончательно получаем 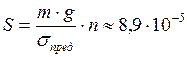 м2.
м2.
Относительное удлинение прутка 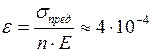 .
.
ЗАДАЧА № II.133Найти потенциальную энергию проволоки длиной 5 см и диаметром 4·10 –3 см, закрученной на угол 10/. Модуль сдвига материала проволоки равен 5,9·1011 дин/см2.
Дано: 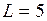 см
см 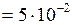 м;
м;
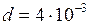 см
см 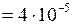 м;
м;
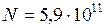 дин/см2
дин/см2 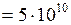 Па;
Па;
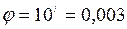 рад.
рад.
Найти: 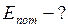
Решение
Для поворота проволоки на угол 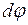 надо совершить работу
надо совершить работу
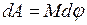 , где
, где 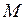 – закручивающий момент. Так как
– закручивающий момент. Так как 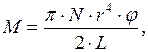
то 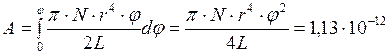 Дж.
Дж.
Эта работа перейдёт в потенциальную энергию 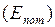 закрученной проволоки.
закрученной проволоки.
ЗАДАЧА № II.134Какое количество теплотыпотребуется для превращения 0,8 кг льда, взятого при температуре –10 0С, в пар при 100 0С (рис.43)? Показать на графике зависимость 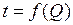 .
.
Дано: 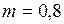 кг;
кг;
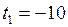 0C;
0C;
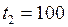 0C;
0C;
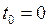 0C;
0C;
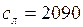 Дж/(кг·К);
Дж/(кг·К);
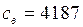 Дж/(кг·К);
Дж/(кг·К);
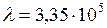 Дж/кг;
Дж/кг;
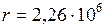 Дж/кг.
Дж/кг.
Найти: 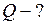

Рисунок 43 - График зависимости 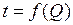
Решение
Искомое количество теплоты определяется суммой количеств теплоты:
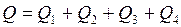 ,
,
где 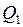 – теплота, необходимая для нагревания льда до температуры плавления
– теплота, необходимая для нагревания льда до температуры плавления
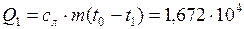 Дж
Дж 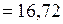 кДж
кДж
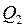 – теплота, необходимая для плавления льда
– теплота, необходимая для плавления льда
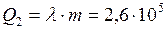 Дж
Дж 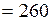 кДж
кДж
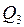 – теплота, необходимая для нагревания полученной воды до точки кипения
– теплота, необходимая для нагревания полученной воды до точки кипения 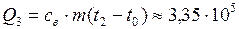 Дж
Дж 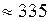 кДж
кДж
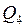 - теплота, необходимая для превращения воды в пар
- теплота, необходимая для превращения воды в пар
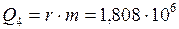 Дж.
Дж. 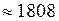 кДж
кДж
Общее количество теплоты, необходимое для превращения льда в пар
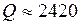 кДж.
кДж.
ЗАДАЧА № II.135Какую наименьшую скорость должен иметь железный метеор, чтобы, попав в атмосферу Земли, он полностью испарился? Начальную температуру метеора перед входом в атмосферу принять равной 3 К. Считать, что 50% кинетической энергии метеора превращается во внутреннюю его энергию.
Дано: 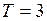 К;
К;
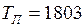 К;
К;
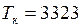 К;
К;
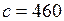 Дж/(кг·К);
Дж/(кг·К);
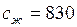 Дж/(кг·К);
Дж/(кг·К);
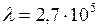 Дж/кг;
Дж/кг;
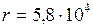 Дж/кг;
Дж/кг;
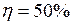 .
.
Найти: 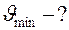
Решение
По условию задачи веществом метеора является железо, поэтому все табличные данные взяты для железа.
Когда метеор попадает в атмосферу Земли, его кинетическая энергия тратится на нагревание, плавление и превращение в пар вещества метеора. По условию задачи на эти процессы расходуется 50% кинетической энергии метеора, следовательно, можно записать
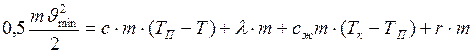 .
.
Исключим из уравнения массу метеора, для этого в правой части уравнения вынесем её за скобки и произведём сокращение
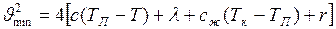 .
.
Запишем решение в общем виде и произведём вычисления
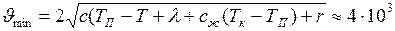 м/с.
м/с.
ЗАДАЧА II.136Медный стержень длиной 1 м и площадью поперечного сечения 1 мм2 нагревается от 200 С до 1000 С, удлиняясь при этом на 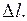 Оценить работу упругих сил при растяжении на величину теплового удлинения
Оценить работу упругих сил при растяжении на величину теплового удлинения 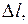 сравнить эту работу с затраченным на нагревание теплом, приняв на этом интервале температуры постоянными: плотность меди
сравнить эту работу с затраченным на нагревание теплом, приняв на этом интервале температуры постоянными: плотность меди
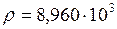 кг/м3 , температурный коэффициент линейного расширения
кг/м3 , температурный коэффициент линейного расширения 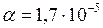 С-1, удельную теплоемкость меди
С-1, удельную теплоемкость меди 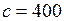 Дж/(кг·К), и модуль Юнга
Дж/(кг·К), и модуль Юнга 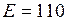 ГПа.
ГПа.
Дано: 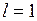 м;
м;
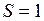 мм2
мм2 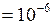 м2;
м2;
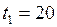 0C;
0C;
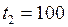 0C;
0C;
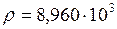 кг/м3;
кг/м3;
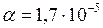 С-1
С-1 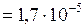 К;
К;
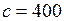 Дж/кг·К;
Дж/кг·К;
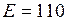 ГПа
ГПа 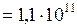 Па.
Па.
Найти: 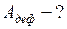
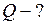
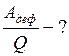
Решение
Удлинение проволоки при тепловом расширении вычисляется по формуле
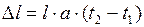 (1)
(1)
Подставив численные значения, получим 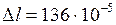 м.
м.
Дата добавления: 2016-09-06; просмотров: 3605;











