Изотермы адсорбции на неоднородной поверхности

Представления о неоднородной поверхности было впервые выдвинуты в работах Теллера^(*), Брунауэра^(*) и развиты Фрумкиным^(*), Тёмкиным^(*) и др. учеными.

Было показано, что теплота адсорбции не постоянна и почти всегда уменьшается с увеличением степени заполнения поверхности.

Если бы все центры адсорбции поверхности были энергетически эквивалентны (поверхность однородна), то дифференциально-молярная теплота адсорбции q по мере заполнения поверхности q не изменялась бы (линия 1 на рис.2.22).

Снижение теплоты адсорбции по мере увеличения степени заполнения поверхности объясняют двумя причинами:

а) биографическая неоднородность — первоначальная неоднородность: выход на поверхность различных кисталлографических граней, ребер, узлов, мест включения примесей и т.д.

б) индуцированная неоднородность связана с самим процессом адсорбции из-за электростатического взаимодействия адсорбированных частиц, вызванного появлением одноименных зарядов; изменением электронной структуры адсорбента вследствие изменения концентрации свободных электронов или протонов на поверхности и смещения уровня Ферми.

По мере заполнения поверхности усиливается взаимное отталкивание адсорбированных частиц (т.н. латеральные взаимодействия), в результате чего каждой новой частице приходится затрачивать на адсорбцию больше энергии, чем предыдущим, и поэтому энергия, выделяющаяся в форме теплоты, уменьшается.

Таким образом, как неоднородность поверхности, так и взаимодействие адсорбированных частиц приводит к зависимости q_адс от степени заполнения поверхности адсорбента (рис.2.22).

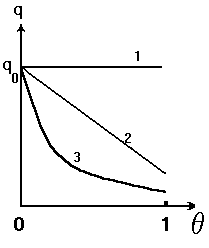
Рис.2.22. Зависимость дифференциальной теплоты адсорбции q от степени заполнения поверхности q.

.

1 - Прямая 1отвечает условию теории Ленгмюра о независимости теплоты адсорбции от степени заполнения поверхности.

2 – В первую очередь адсорбция идет на центрах более ненасыщенных ("жадно" адсорбирующих) с выделением максимальной теплоты q_o. Далее заполняются центры, слабее адсорбирующие, и выделяющаяся теплота по мере их покрытия снижается. Линейная зависимость q_st от q (линия 2) означает, что центров всех сортов на поверхности примерно одинаково.

q=f(Θ); q= q_о – k Θ (2.66)

Для равномерно неоднородной поверхности (примерно одинаковое число всех центров адсорбции) уравнение изотермы, полученное М.И. Тёмкиным, имеет вид:

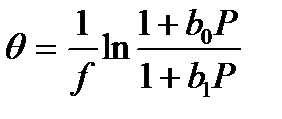, (2.67)

где f - показатель неоднородности, равный ln(b₀/b₁). При больших значениях Р, когда b₀×P >> 1 и b₁×P >> 1, пренебрегая 1 по сравнению с b₀×P и b₁×P, получаем 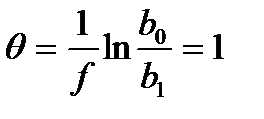, (2.68)

т.е. имеет место насыщение поверхности.

Напротив, при малых Р, когда b₀×P << 1 и b₁×P << 1, разлагая ln(1+b₀P) и ln(1+b₁P) в ряд и ограничиваясь первым членом ряда, получаем 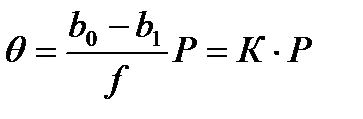, (2.69)

т.е. приходим к линейной изотерме Генри.

Для средних заполнений поверхности уравнение трансформируется в:

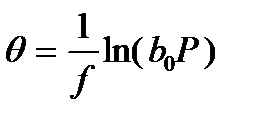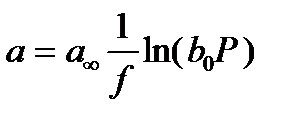или , (2.70)

Эти изотермы адсорбции в литературе называют логарифмической изотермой или изотермой Тёмкина.

3. – Кривая 3 на рис.2.22 соответствует тому случаю, когда сильно адсорбирующих центров на поверхности мало, а большинство центров адсорбируeт слабо (с выделением малой теплоты). Адсорбция на экспоненциально неоднородной поверхности, описывается эмпирическим уравнением, впервые предложенным Фрейндлихом^(*) (изотерма Фрейндлиха):

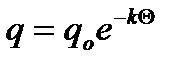, (2.71)

в котором k=f(T, природы адсорбента и адсорбата).

Как показал Зельдович⁽³¹⁾ в области средних заполнений

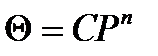, где С и n — константы, 0<n<1. (2.72)

Чаще всего это уравнение используют в логарифмической линейной форме:

lnA=lnk + n lnP, (2.73)

k — адсорбционный показатель, зависит от природы адсорбента и Т; с увеличением Т уменьшается, а n растет.

Следует иметь в виду, что изотерма вида (2.71) не может описать всю реальную изотерму адсорбции. Действительно, при полном покрытии всех центров адсорбции а = а_¥, т.е. в области больших Р обычно наблюдают независимость адсорбции от давления, а рассматриваемое уравнение предсказывает бесконечное увеличение а с ростом давления.И наоборот, при малых Р эксперименты дают линейную связь а и Р (изотерма Генри). Уравнение же лишь с определённой погрешностью может быть аппроксимировано в линейную зависимость. По этой причине сложилось мнение, что изотерма Фрейндлиха справедлива лишь в интервале средних концентраций адсорбата.

2.4.3. Теории полимолекулярной адсорбции

а) теория Поляни^(*)

Возможность образования полимолекулярных слоев в пористых адсорбентах рассматривается в потенциальной теории Поляни.

Эта теория была предложена для термодинамического описания полимолекулярной адсорбции. Она устанавливает связь величины адсорбции с давлением адсорбата и дифференциальной теплотой адсорбции. Наиболее удачно она предсказывает зависимость величины адсорбции как функции температуры.

Теория не приводит к конкретным уравнениям, но широко используется для описания адсорбции на пористых адсорбентах, т.к. часто эта зависимость А=f(Р) имеет вид:

_А

1 Р/Р_о

Рис. 2.23. Изотерма полимолекулярной адсорбции

Основные положения теории Поляни:

1. Адсорбция обусловлена чисто физическими силами взаимодействия.

В адсорбционном пространстве действуют только дисперсионные силы, не зависящие от температуры. На поверхности адсорбента нет активных центров, а адсорбционные силы образуют около поверхности адсорбента непрерывное силовое поле. Адсорбционные силы действуют на расстоянии, большем, чем диаметр отдельной молекулы.

При адсорбции характер взаимодействия между молекулами адсорбата не изменяется, а происходит увеличение его плотности на поверхности адсорбента. Силы по мере удаления от поверхности на некотором расстоянии от нее становятся равными 0.

2. Всё адсорбированное вещество на поверхности находится в жидком состоянии. Объём, занимаемый адсорбатом, равен

V_ж.адс.=АV_м . (2.74)

3. За меру интенсивности адсорбционного взаимодействия принят адсорбционный потенциал, работа переноса 1 моль газа с поверхности жидкого адсорбата (р_о) в равновесную газовую фазу (р):

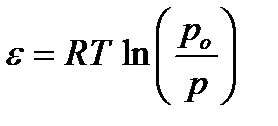, (2.75)

он характеризует работу против внешних вил.

С приближением к поверхности адсорбента адсорбционные возрастают, а потом уменьшаются, доходя до 0 и переходя в силы отталкивания. Таким образом создаётся адсорбционное поле, каждой точке которого соответствует определенное значение адсорбционного потенциала ε.

Молекулы газа, попадая в адсорбционное поле, притягиваются поверхностью адсорбента. Образуется полимолекулярный слой, плотность которого уменьшается по мере удаления от поверхности.

Адсорбционный слой напоминает атмосферу: вблизи поверхности твердого тела он сжат, а в наружных слоях — разрежен. Представление о потенциальном поле дают эквипотенциальные поверхности

поверхности одинакового потенциала

Расстояние между каждой парой эквипотенциальных поверхностей соответствует некоторому объёму, поэтому между потенциалом ε и V существует определенная зависимость.

В адсорбционном пространстве действуют дисперсионные силы, которые не зависят от температуры. Каждой точке изотермы адсорбции соответствуют определенные значения А и Р/Р_о, которая позволяет получать значения ε и V, зависимость ε=f(Т) и заменить зависимость ε=f(r) на ε=f(V_ж.адс.). Зависимость ε=f(r) называется потенциальной кривой адсорбции. Ее можно построить, исходя из экспериментально полученной изотермы адсорбции, зная распределение V_ж.адс по адсорбционному пространству:

ε

V

Рис. 2.24. Потенциальная кривая адсорбции

Пользуясь этой зависимостью, можно построить изотерму при любой температуре, получив изотерму адсорбции при одной температуре Т₁.

Так как дисперсионные силы не зависят от температуры, то от температуры не должна зависеть и форма потенциальной кривой адсорбции, что подтверждается и экспериментально. Экспериментальные точки при разных температурах ложатся на одну и ту же зависимость ε=f(V_ж.адс.), которую называют характеристической кривой: 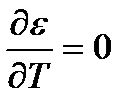. (2.76)

Для двух температур: V=А₁V_М1 = А₂V_М2 (2.77)

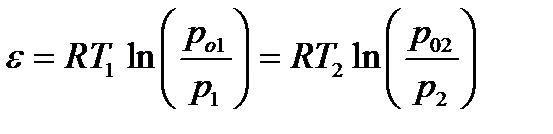(2.78)

_{а lnP}

Т_{1 α} α=-q_st / R

Т₂

_{Р 1/T}

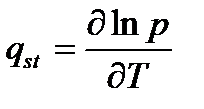_, исходя из уравнения Клаузиуса—Клапейрона^(33,34) 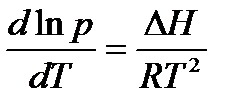(2.79)

Рис.2.25. Построение и расчент изотерм адсорбции из одной изотермы по теории Поляни

Важное свойство было обнаружено Дубининым^(*):

Характеристические кривые для одного и того же адсорбента и разных адсорбатов при всех значениях объёма адсорбата в поверхностном слое находятся в постоянном соотношении: β=(ε/ ε_о)_V, где β — коэффициент аффинности.

Отсюда следует, что, зная характеристическую кривую для одного адсорбата и β для другого по отношению к первому, можно вычислить изотерму адсорбции для 2-го адсорбата на том же адсорбенте.

Теория Поляни не дала математического выражения для изотермы адсорбции, однако ее представления положены в основу и используются современной теорией объёмного заполнения пор молекулами адсорбата. Она не потеряла практического значения и остается теорией, пригодной для описания адсорбции на адсорбентах с резкой энергетической неоднородностью (на углях).

Мы познакомились с двумя теориями адсорбции газов и паров на поверхности твердых адсорбентов — Ленгмюра и Поляни, очень по-разному подходящих к рассмотрению этого процесса. Возникает вопрос, какой отдать предпочтение. Обе они ограничены в применении.

Теория Поляни применима к физической адсорбции молекул адсорбата, теория Ленгмюра охватывает с известными ограничениями и физическую, и химическую адсорбцию адсорбата. Однако она не может быть применима для объяснения адсорбции на пористых адсорбентах с мелкими порами из-за резкой энергетической неоднородности поверхности. Делались попытки обобщить представления Ленгмюра и Поляни. Такая обобщенная теория была развита Брунауэром, Эмметом^(*) и Теллером в 1935-40-х гг. прошлого века применительно к адсорбции паров.

.

Б)Теория БЭТ

Брунауэр, Эммет и Теллер создали наиболее общую теорию полимолекулярной адсорбции, в которой описание процессов адсорбции увязывается с представлениями и методами статистической физики.

Авторы теории на основе уравнения Ленгмюра получили приближенное уравнение полимолекулярной адсорбции, которое широко применяется для определения удельной поверхности адсорбента и теплоты адсорбции.

В теории рассматривается адсорбция паров и газов при Т< Т_кр.с образованием полимолекулярного слоя вещества на поверхности адсорбента. При Р=Р_о идет конденсация пара.

Уравнение Ленгмюра можно использовать только при отсутствии адсорбции веществ сверх монослоя. Это строго: при хемосорбции, физической адсорбции газов при малых Р и Т>Т_кр и адсорбции веществ из растворов. Чаще образуются полислои.