И ПЕРЕХОДНЫХ СОСТОЯНИЙ
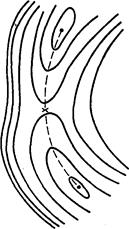
Для получения наиболее полной информации о механизме реакции необходимо вычислить многомерную поверхность потенциальной энергии (ППЭ), т.е. рассчитать зависимость полной энергии от координат атомных ядер. Наиболее интересными и важными при изучении механизма реакции являются так называемые стационарные точки на ППЭ. Под этим термином понимают минимумы и седловые точки на ППЭ (рис. 1.4). В стационарных точках производные полной энергии Е по всем независимым координатам хi равны нулю:
gi = ∂E/∂xi =0 (для любого i).
В точке минимума полной энергии матрица вторых производных fij = ∂2E/∂xi ∂xj имеет только положительные собственные значения, а в седловой точке - одно отрицательное собственное значение. Минимумы полной энергии соответствуют устойчивым структурам и интермедиатам, а седловые точки — переходным состояниям.
Основная трудность, с которой мы сталкиваемся при расчете ППЭ для органических реакций с участием многоатомных молекул, заключается в необходимости вычисления полной энергии реагентов для очень большого числа точек.
Рис. 1.4. Стационарные точки на ППЭ
а — минимум локальный или глобальный;
б — седловая точка
 
| Рис. 1.5. Простейшая ППЭ
Темные кружки – исходные реагенты
и продукты реакции;
крестик — переходное состояние.
|
Если в реагентах содержится лишь 10 атомов (обычно их значительно больше), то их положение в пространстве для нелинейной системы описывается 24 независимыми координатами. Для надежного построения полной ППЭ для каждой независимой координаты необходимо взять по крайней мере около 10 точек, таким образом полную энергию необходимо вычислить около 1024 раз. Это невероятно большая величина, и такое количество вычислений проделать практически невозможно. Поэтому при построении ППЭ обычно варьируют не все независимые степени свободы, а лишь некоторые из них, чаще всего один или два геометрических параметра, которые наиболее сильно меняются в ходе реакции, а по всем остальным степеням свободы проводят оптимизацию, т.е. находят их оптимальные значения (соответствующие минимуму полной энергии) для каждой точки ППЭ. Для разделения всех степеней свободы на те, которые надо варьировать, и те, которые можно оптимизировать, используют химическую интуицию. Переход от варьирования к оптимизации для большинства степеней свободы при построении ППЭ позволяет очень сильно сократить затраты машинного времени и делает расчет ППЭ практически возможным для реакций с участием достаточно больших органических соединений.
Типичный вид простейшей двумерной ППЭ показан на рис. 1.5. Здесь минимумы соответствуют исходным реагентам и конечным продуктам реакции, а седловая точка - переходному состоянию. Минимумы на рисунке соединены пунктирной линией, которая проходит по дну долины на ППЭ через седловую точку. Эта линия показывает путь реакции в двумерном (в общем случае многомерном) пространстве или траекторию движения реагентов в ходе реакции.
На рис. 1.5. показана простейшая ППЭ. Для большинства реакций ППЭ имеют более сложный вид. На них может быть более двух глубоких минимумов, которые соответствуют исходным реагентам и различным конечным продуктам реакции (если реакция может идти по нескольким направлениям). Кроме того, может быть несколько мелких локальных минимумов, соответствующих интермедиатам. Реакция может идти по нескольким траекториям через разные переходные состояния и приводить к разным конечным продуктам. При вычислении константы скорости k = koexp(-Eакт/RT) элементарных реакций с участием органических молекул обычно пользуются теорией переходного состояния. В рамках этой теории для вычисления энергии активации Еакт и предэкспоненты kо необходимо знать потенциальную энергию, геометрию, а также полный набор колебательных частот исходных реагентов и переходного состояния.
Для бимолекулярной реакции
А + В → АВ# → С + D
ko = kБTQ#/(hQAQB),
где kБ и h - универсальные постоянные; Т - температура; QA, QB и Q# - статистические суммы исходных реагентов А и В и переходного состояния АВ#.
Каждая из этих статистических сумм является произведением трансляционной, вращательной и колебательной статистических сумм
Q = Qтр Qвр Qкол;
Qтр = [mkБT/(2πh2)]3/2,
где m — масса молекулы или переходного состояния;
Qвр = π7/2(8kБТ/h2)3/2(IAIBIC)1/2
где IА, IB и IC - моменты инерции;
Qкол = Пi(1 - ехр(hνi/kБТ)
где νi — колебательные частоты (произведение берется по всем колебательным степеням свободы).
Для вычисления энергии активации Еакт и предэкспоненты ko по теории переходного состояния необходимо знать геометрию, потенциальную энергию и полные наборы колебательных частот соединений А, В и переходного состояния. Геометрия нужна для определения моментов инерции в формуле для Qвр, значения потенциальной энергии - для расчета Еакт, колебательные частоты - для вычисления вклада энергии нулевых колебаний в Еакт и колебательной статсуммы Qкол.
Таблица 1.9 Вычисленные энергии активации (кДж/моль) для реакций, приведенных на схемах I - V [56]
| Реакция | МПДП | КМПДП | ХФ | КХФ* |
| — | ||||
| — | ||||
*При расчете энергии активации использована геометрия переходного состояния, предварительно вычисленная в приближении Хартри—Фока.
Таким образом, мы видим, что для определения константы скорости реакции нет необходимости рассчитывать всю ППЭ. Достаточно найти на ней лишь стационарные точки. Геометрию исходных реагентов для любой реакции можно найти с помощью минимизации полной энергии. Эту задачу сравнительно легко решить. Гораздо сложнее найти геометрию переходного состояния. Переходные состояния являются седловыми точками на ППЭ. Они похожи на минимумы, поскольку в них, как и в минимумах, градиент полной энергии по координатам равен нулю, но их нельзя найти с помощью минимизации полной энергии. В работе [55] было предложено искать переходные состояния с помощью минимизации квадрата модуля градиента, т.е. минимизировать сумму квадратов производных полной энергии по всем независимым координатам:
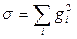
Минимизация этого выражения действительно позволяет найти переходные состояния, однако сделать это достаточно сложно. Выражение для σ имеет очень много минимумов, так как не только стационарные точки дают минимумы для σ, но и любой изгиб ППЭ типа плеча приводит к появлению минимума для этой величины. Поэтому предложенная методика [55] пригодна лишь в непосредственной близости от седловой точки, и основная трудность при расчете геометрии переходных состояний этим методом заключается в том, что исходная (стартовая) геометрия, с которой начинается поиск, должна быть достаточно близка к конечной (истинной) геометрии переходного состояния. Определять стартовую геометрию приходится на основе интуитивных соображений, так как из эксперимента получить хотя бы приближенную информацию о геометрии переходных состояний невозможно. Поэтому успешный поиск переходных состояний с помощью минимизации выражения для σ в значительной степени зависит от опыта исследователя.
Наибольший интерес вызывает вопрос о точности, с которой можно рассчитать геометрию переходного состояния и энергию активации методами квантовой химии. К сожалению, мы не располагаем достаточно полным набором данных эксперимента по энергиям активации для различных типов реакций с участием маленьких молекул, а экспериментальные значения геометрических параметров переходных состояний получить невозможно. Поэтому в настоящем разделе нам пришлось ограничить рассмотрение вопроса о точности расчета переходных состояний методами квантовой химии сопоставлением результатов, которые были получены полуэмпирическими и неэмпирическими методами (см. [56, 57] и ссылки в них).
В табл. 1.9 и 1.10 сопоставлены данные расчета параметров переходных состояний для реакций, изображенных на схемах I—V (см. стр. 40), методами МПДП и КМПДП (метод МПДП с учетом электронной корреляции), неэмпирическим методом в приближении Хартри-Фока без учета и с учетом электронной корреляции.
В таблицах неэмпирический расчет в приближении Хартри-Фока без учета электронной корреляции обозначен ХФ, с учетом электронной корреляции - КХФ [56, 57].
Таблица 1.10 Статистический анализ результатов расчета геометрии переходных состояний и энергий активации методами МПДП и КМПДП [56, 57]
| Вычисленная величина | Число расчетов | Абсолютная ошибка*1 | |
| МПДП | КМПДП | ||
| Длина валентных связей*2, нм из них активных*3 пассивных*3 Валентный угол*2, град Торсионный угол*2, град Энергия активации, кДж/моль | 0,0057 0,0078 0,0018 7,9 11,6 90*4 | 0,0056 0,0073 0,0025 6,2 7,9 36*4 |
*1 По сравнению с данными неэмпирического расчета в приближении Хартри-Фока.
*2 Для переходного состояния.
*3 Активные связи разрываются или образуются в ходе реакции, пассивные связи в ходе реакции формально остаются неизменными.
*4 По сравнению с данными неэмпирических расчетов с учетом электронной корреляции.
Для реакций, изображенных на схемах I - III, расчеты с оптимизацией геометрии в приближении Хартри-Фока проведены в базисе 6-31ГФ*, для реакций, изображенных на схемах IV и V, - в базисе 3-21ГФ или 4-31ГФ. Электронная корреляция учитывалась только при вычислении энергии активации. Эти расчеты проведены по теории возмущений Мёллера-Плезетта с точностью до четвертого порядка включительно или в приближении связанных электронных пар.
Схема I Схема II Схемa III
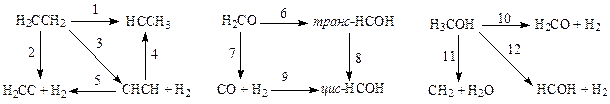
Схема IV Схемa V
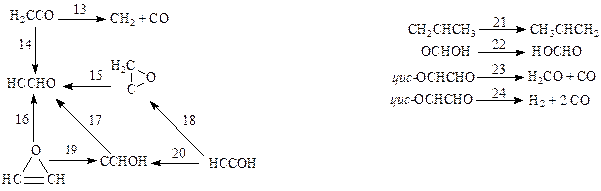
Из этих данных видно, что геометрические параметры переходных состояний, вычисленные методами МПДП и КМПДП, находятся в хорошем согласии с данными неэмпирических расчетов без учета электронной корреляции. Однако для длин валентных связей, которые формально разрываются или образуются в ходе реакции (активные связи), расхождение результатов, полученных полуэмпирическими и неэмпирическими методами, заметно больше, чем для валентных связей, которые в ходе реакции остаются формально неизменными (пассивные связи). Сопоставить результаты расчета геометрии переходных состояний методами МПДП и КМПДП с данными неэмпирических расчетов с учетом электронной корреляции невозможно из-за почти полного отсутствия в литературе последних. При расчете энергий активации величины, полученные методами МПДП и КМПДП, отличаются на 15 - 20% от значений, вычисленных неэмпирическим методом без учета электронной корреляции. При сравнении с данными неэмпирических расчетов с учетом электронной корреляции оказывается, что метод КМПДП дает более близкие результаты. Это, по-видимому, связано с выбором реакций для тестирования. В отобранных реакциях учет электронной корреляции может заметно изменить результаты расчета, так как для сравнения авторам работ [56, 57] пришлось взять лишь те химические превращения, для которых из литературы были известны результаты вычислений неэмпирическими методами с использованием достаточно большого базиса и с учетом электронной корреляции. Такие расчеты, естественно, были опубликованы лишь для тех реакций, в которых электронная корреляция играет существенную роль. Для других типов реакций литературные данные отсутствуют, и их получение связано с очень большим объемом вычислений.
Таблица 1.11
Вычисленные тепловой эффект Q и энергия активации Н# реакции (25) (кДж/моль)
| Метод | Q | H# | H#обр |
| ХФ/3-21ГФ ХФ/6-31ГФ* МП2/6-31ГФ* МПЗ/6-31ГФ* МПЗ/6-311ГФ** МП4/6-311ГФ** С учетом нулевых колебаний |
Примечание. Использованы следующие обозначения: ХФ — расчет в приближении Хартри-Фока; МП2, МПЗ и МП4 — расчеты с учетом электронной корреляции во втором, во втором и третьем и во втором, третьем и четвертом порядках теории возмущений Меллера-Плезетта. В методах МПЗ/6-31ГФ**, МПЗ/6-311ГФ** и МП4/6-311ГФ** использована геометрия, вычисленная предварительно методом МП2/6-31 ГФ*; Нобр - энергия активации обратной реакции.
Некоторое представление о влиянии базиса и электронной корреляции на результаты неэмпирических расчетов высоты активационных барьеров можно получить из табл. 1.11 и 1.12, в которых приведены данные для реакций
HC≡CH → H2C=C: (25),
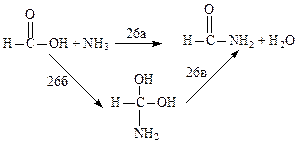
Для реакции (25) зависимость достаточно сильная [58-60], для (26) - слабая [61]. Существенное влияние электронной корреляции на результаты расчета высоты активационных барьеров можно ожидать для реакций, в ходе которых образуются бирадикалы, карбены и родственные им структуры. Кроме того, электронную корреляцию обязательно надо учитывать при расчете ППЭ для реакций гомолитического разрыва валентных связей.
Таблица 1.12 Энергии активации реакций (26) (кДж/моль) [61]
| Метод | (26а) | (26б) | (26в) | Метод | (26а) | (26б) | (26в) |
| ХФ/3-21ГФ МП2/3-21ГФ ХФ/6-31ГФ МП2/6-31ГФ ХФ/6-31ГФ* | МП2/6-31ГФ* ХФ/6-31ГФ** МП2/6-31ГФ** МПЗ/6-31ГФ** МП4/6-31ГФ** |
Примечание. Обозначения те же, что и в предыдущей таблице. Во всех расчетах использована геометрия молекул и переходных состояний, вычисленная предварительно методом ХФ/3-21ГФ.
Вопрос о влиянии электронной корреляции на геометрию переходных состояний был рассмотрен в работе [62]. В ней методом МПДП без учета и с учетом электронной корреляции была рассчитана геометрия переходных состояний для реакций, изображенных на схемах I - V, и показано, что учет электронной корреляции изменяет межатомные расстояния в среднем не более чем на 0,003 нм, при этом изменения длины активных валентных связей, т.е. тех, которые разрываются или образуются в ходе реакции, не превышают 0,004 нм, а пассивных, т.е. тех, которые в ходе реакции остаются формально теми же, 0,001 нм, валентные углы меняются менее чем на 3°. Эти небольшие изменения геометрических параметров незначительно меняют структуру переходного состояния и практически не сказываются на результатах расчета энергии активации. На основе этих данных в работе [62] был сделан вывод о том, что корреляционные эффекты можно не учитывать при квантовохимических расчетах геометрии переходных состояний. Аналогичных исследований, выполненных неэмпирическими методами, в настоящее время нет.
Дата добавления: 2020-12-11; просмотров: 470;











