Аналитический метод исследования переходных процессов электропривода на базе математической модели двигателя постоянного тока

Для исследования переходных процессов прямого пуска двигателя постоянного тока воспользуемся уравнениями (23) - (27), выведенными в разделе 2.

L_яdi_я/dt +i_я(R_я +R_д)= U_я -e_я ;

L_вdi_в/dt +i_вR_в=U_в;

JdΩ/dt= M_дв -M_нг ;

;

;

;

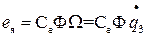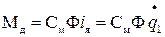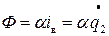M_нг=M(Ф; Ω; p; t …).

Примем допущения: поток Ф=соnst = Ф_N, внутреннее сопротивление сети и дополнительное сопротивления цепи обмотки якоря R_д равны нулю. Уравнение равновесия напряжения цепи обмотки возбуждения можно не учитывать.

Тогда система уравнений для исследования процесса пуска может быть представлена в виде:

L_яdi_я/dt +i_яR_я= U_я -С_еФΩ ; (131)

JdΩ/dt= M_дв -M_нг =С_мФi_я - М_нг. (132)

Эта система уравнений является основной для рассмотрения переходных процессов по скорости, току и моменту, т.е. по наиболее существенным координатам, характеризующим состояние движения в переходных процессах.

Выразим из уравнения (132) ток якоря

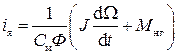. (133)

Продифференцируем полученное выражение тока якоря:

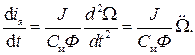
Подставим это выражение производной тока в уравнение (131):

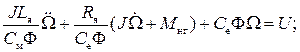
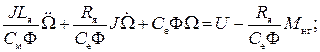
Избавимся от коэффициента при старшей производной и получим дифференциальное уравнение второго порядка

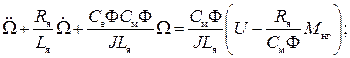(134)

Обозначим

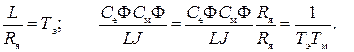
Обозначим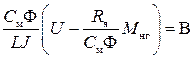

Уравнение (134) примет вид

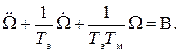(135)

Решение линейного дифференциального уравнения второго порядка (135) содержит две составляющие - свободную составляющую Ω₁(t) и вынужденную составляющую Ω₂(t):

Ω (t)= Ω₁(t)+ Ω₂(t). (136)

Свободная составляющая Ω₁(t) характеризует собственные динамические свойства объекта, описываемые левой частью уравнения, и показывает как объект будет вести себя, если его вывести из состояния равновесия. Она определяется решением левой части уравнения (135). При этом правая часть уравнения принимается равной 0.

Вынужденной составляющей Ω₂(t) определяется правой частью уравнения (135) и характеризует величину установившегося значения скорости вращения при заданных параметрах двигателя, нагрузки и напряжения источника питания. Для определения составляющей Ω₂(t) необходимо в уравнении (134) приравнять нулю первую и вторую производные скорости.

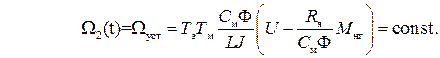(137)

Для определения Ω₁(t) необходимо решить характеристическое уравнение, записанное по левой части уравнения (135)

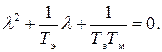
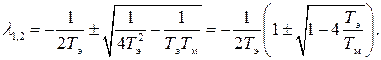(138)

Характер переходных процессов рассматриваемой системы зависит от соотношения постоянных времени этой системы Т_м и Т_э . Возможно три варианта соотношения постоянных времени Т_м и Т_э.

Вариант 1: Т_м<4Т_э.

При таком соотношении постоянных времени системы корни характеристического уравнения разные, комплексные: .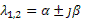

Свободная составляющая скорости вращения

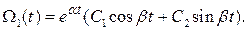
Вынужденная составляющая Ω ₂(t)=Т_мТ_эВ= Ω _уст.

Полное выражение для скорости вращение при прямом пуске для случая Т_м<4Т_э

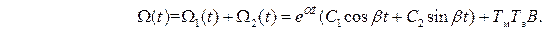
Переходный процесс имеет вид затухающих гармонических колебаний вдоль уровня, соответствующего установившемуся значению скорости.

Вариант 2: Т_м=4Т_э.

При таком соотношении постоянных времени системы корни характеристического уравнения одинаковые, вещественные: λ₁= λ₂= λ.

В этом случае свободная составляющая скорости имеет вид

Ω ₁(t)=e^λt (C₁+C₂t), а полное решение

Ω (t)= Ω ₁(t)+ Ω ₂(t)=e^λt (C₁+C₂t) +Т_мТ_эВ.

Характер переходного процесса асимптотический.

Вариант 3: Т_м>4Т_э .

При таком соотношении постоянных времени системы корни характеристического уравнения λ₁ и λ₂ вещественные, разные.

В этом случае свободная составляющая скорости имеет вид

Ω ₁(t)= C₁e^λ1t +C₂e^λ2t, а полное решение

Ω (t)= Ω₁(t)+ Ω ₂(t)= C₁e^λ1t + C₂e^λ2t +Т_мТ_еВ. (139)

Скорость также как и во втором случае будет нарастать при пуске по асимптоте. В конце пуска скорость достигнет установившееся значение

Ω _уст= T_мT_эB.

Определим переходный процесс тока якоря при прямом пуске для случая соотношения постоянных времени Т_м>4Т_э.

Необходимо продифференцировать выражение для скорости (139) и подставить производную скорости во времени в формулу (133)

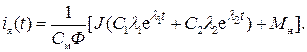
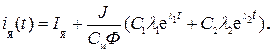
Определим постоянные интегрирования С₁ и С₂.

Для этого, запишем уравнение (139) для начальных условий (t=0):

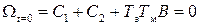(140)

Производная скорости при t=0

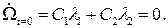(141)

Решая уравнения (140) и (141), получим значения постоянных С₁ и С₂

(142)

На обмотку якоря скачком подается напряжение U.

Если Т_э<<Т_м графики скорости и тока при прямом пуске можно строить по упрощенным формулам, приняв Т_э=0.

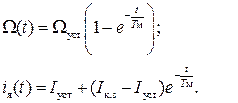(143) Проанализируем вид переходного процесса скорости и тока якоря при прямом пуске для двух вариантов: Т_э=0 и Т_э≠0.

Рассматривая графики скорости и тока якоря (см. рис.61, а и б), можно отметить, что при отсутствии индуктивности в цепи обмотки якоря (Т_э=0) ток якоря в момент пуска скачком достигает своего максимального значения I_кз=U_я/R_я. При наличии индуктивности в цепи обмотки якоря (Т_э=0) ток якоря при прямом пуске нарастает по экспоненте и достигает максимального значения I_max< I_кз.

Скорость вращения при прямом пуске при Т_э=0 нарастает по экспоненте, а при Т_э≠0 в переходном процессе скорости появляется задержка и график скорости на начальном этапе пуска принимает так называемую форму «лыжи».

.

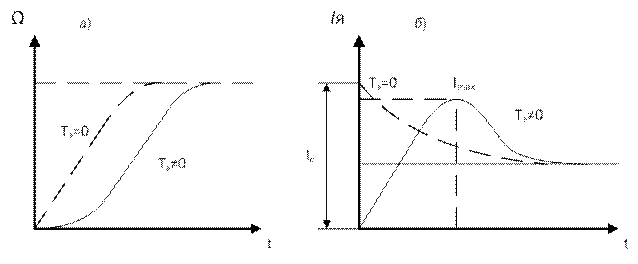
Рис.61.Графики изменения скорости (а) и тока (б) во времени при прямом пуске двигателя постоянного тока без учета электромагнитной постоянной времени (Т_э=0) и с учетом электромагнитной постоянной времени (Т_э≠0).

Вопросы для самоконтроля

1.Напишите исходные уравнения для исследования переходных процессов пуска двигателя постоянного тока в ход.

2.Укажите влияние соотношения постоянных времени двигателя Т_м и Т_э на характер переходных процессов пуска двигателя ход.

3. Нарисуйте графики переходных процессов тока якоря и скорости вращения при пуске двигателя в ход с учетом и без учета электромагнитной постоянной времени Т_э.