Диссоциация молекул в полярных растворителях
Рассмотрим вопрос о механизме диссоциации молекул в полярных растворителях. Химики-экспериментаторы очень часто имеют дело с такими процессами при изучении многих органических реакций, поэтому необходимо уметь их моделировать в квантовохимических расчетах. На первый взгляд эта задача кажется очень простой, однако при более близком знакомстве с ней выясняется, что механизм этих процессов весьма сложен и общепринятые представления о нем являются неточными. В квантовохимических работах образование ионов в полярных растворителях наиболее часто рассматривалось на примере следующей модельной реакции [116]:
FH + NH3 → F- + NH4+. (I)
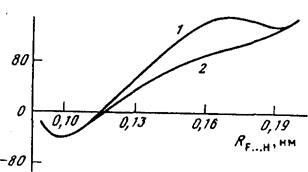
FH - кислота, a NH3 - основание, поэтому в водных растворах эта система должна существовать в ионной форме F- + NH4+. Однако в квантохимических расчетах удавалось получить лишь локальный минимум для ионной пары и то только при фиксированном и достаточно большом расстоянии между атомами фтора и азота. Включение этого расстояния в число варьируемых параметров неизменно приводило к исчезновению локального минимума для ионизированной системы. В качестве примера на рис. 2.1 приведены результаты такого расчета методом МПДП/Н, сольватация моделировалась в приближении супермолекулы шестью молекулами воды.
Рис. 2.1. Сечение ППЭ для реакции переноса протона (I)
1 - расстояние между атомами F и N фиксировано;
Расстояние между атомами F и N оптимизировано
Е, кДж/моль
Е, кДж/моль
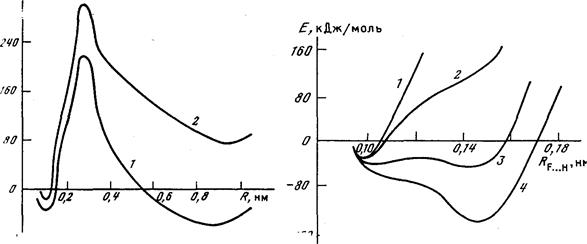
| Рис. 2.2. Сечение ППЭ для реакций переноса протона 1 - реакция (I); 2 – Н2О...Н2О→ОН- + Н3О+. R - расстояние между атомами F—Н или О—Н. Расчет выполнен методом МПДП/Н; для учета сольватации использована модель точечных диполей | Рис. 2.3. Сечение ППЭ для реакции переноса протона (I) Расчет выполнен методом МПДП/Н, для учета сольватации использована модель точечных диполейμ(1030*D/м3): 1 - 0; 2 - 0,06; 3-0,12; 4 - 0,15. |
При дальнейшем исследовании этой системы [116] было установлено, что минимум для электрически нейтральной системы является локальным, а глобальный минимум соответствует разделенной ионной паре, в которой расстояние между ионами составляет около 1 нм (рис. 2.2). Для контактных ионных пар минимума обнаружено не было, что свидетельствует о невозможности их существования в водных растворах.
Из этих данных становится очевидной причина неудачного рассмотрения многими авторами реакций диссоциации молекул в водной среде. Делались попытки найти контактные ионные пары. Модель выбиралась такой, что образование разделенных ионных пар было невозможно. В результате удавалось получить лишь один минимум для электрически нейтральной системы.
Мы привыкли считать, что с увеличением полярности среды на профиле потенциальной энергии реакции диссоциации первоначально образуется минимум для контактной ионной пары и лишь потом - для разделенной. В действительности это не так. Если растворитель можно рассматривать как непрерывную (континуальную) среду, то минимумы (и локальные, и глобальные) на профиле потенциальной энергии для контактных ионных пар будут отсутствовать при любой его полярности. Действительно контактные ионные пары в водных растворах практически не образуются, поскольку молекулы воды почти непрерывно увеличивают размер гидратационной оболочки с ростом напряженности электрического поля растворенного соединения. Для маленьких ионов образуется до трех гидратационных оболочек. Этот эффект непрерывности не позволяет образовываться контактным ионным парам.
Контактные ионные пары могут существовать только в растворителях, которые имеют качественно иную структуру по сравнению с водой и в которых сольватная оболочка не может непрерывно увеличивать свой размер. Например, в ацетонитриле, диметилсульфоксиде и многих других полярных растворителях дипольный момент локализован на одном конце молекулы, а на другом находится неполярная группа большого размера. Для таких растворителей характерны дискретные свойства: после заполнения первого сольватационного слоя происходит резкое уменьшение величины энергии последовательной сольватации и вторая сольватная оболочка практически не формируется.
В модель точечных диполей дискретные свойства сред такого типа можно ввести, например, путем ограничения количества точечных диполей, которые могут взаимодействовать с растворенной молекулой. На рис. 2.3 показаны результаты расчета сечения поверхности потенциальной энергии для реакции переноса протона в предположении, что количество точечных диполей объемом Vт.д= 10-3 нм3 не может превышать 200. Видно, что при таком ограничении количества точечных диполей глобальный минимум соответствует контактным ионным парам. Получить его без введения в использованную сольватационную модель элемента дискретности невозможно.
2.7.2. Реакции нуклеофильного замещения, протекающие по механизму SN2
За последние, годы существенно расширились наши знания о детальных механизмах реакций нуклеофильного замещения, широко распространенных в химии [117, 118]. Методами масс-спектрометрии высоких давлений [119], ионного циклотронного резонанса [120] и квантовой химии [121 - 123] показано, что в газовой фазе первоначально образуется устойчивый предреакционный комплекс (K1). Ему соответствует первый минимум на профиле потенциальной энергии. При дальнейшем движении вдоль координаты реакционная система преодолевает активационный барьер, после чего образуется второй комплекс (К2), который распадается на конечные продукты:
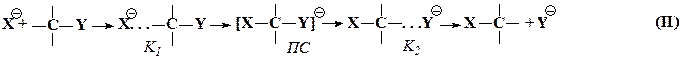
Таблица 2.2
Энтальпия (ΔН) и активационный барьер (Е#) реакции (III) в водном растворе (кДж/моль) [125]
| X | Н | F | Сl | Н | F | Сl | Н | F | Сl |
| Y | Н | Н | Н | F | F | F | Сl | Сl | Сl |
| ΔН | -154 | -17 | |||||||
| Е# |
Экспериментально эти реакции обычно изучаются в растворах. Влияние сольватации на профиль потенциальной энергии было установлено на основе результатов квантовохимических расчетов.
В работе [124] рассчитано сечение поверхности потенциальной энергии для реакции Сl- + Н3ССl → СlСН3 + Сl- неэмпирическим методом 3-21ГФ. Для моделирования сольватации использовано приближение супермолекулы (к реагентам добавлено две молекулы воды). Было показано, что сольватация существенно повышает активационный барьер реакции. Однако вычисленное значение энергии активации оказалось сильно заниженным по сравнению с экспериментом. Это связано, во-первых, с недостаточным количеством молекул воды, включенным в гидратационную оболочку реагентов, и, во-вторых, с использованием базиса 3-21 ГФ, расчеты в котором существенно переоценивают стабильность комплексов K1 и К2 и переходного состояния (ПС) реакции (II) в газовой фазе.
В работе [125] модифицированным методом ППДП/2 вычислен профиль потенциальной энергии для реакций [126],
X- + Н3СY → XСН3 + Y- (X,Y=H,F,Cl) (III)
для учета сольватации использована модель точечных зарядов. Полученные результаты приведены в табл. 2.2, из которой видно, что гидратация качественно изменяет профиль потенциальной энергии исследованных реакций и приводит к появлению активационных барьеров. Их высота, вычисленная квантовохимическим методом, близка к экспериментальным значениям.
В работе [127] профиль потенциальной энергии для реакции
Сl- + Н3ССl → СlСН3 + Сl- (IV)
ОН- + Н3СВr → НОСН3 + Вr- (V)
рассчитан методом МПДП. Для учета гидратации использована модель точечных диполей. Полученные результаты приведены на рисунке 2.4 и в таблице 2.3. Видно, что гидратация существенно изменяет профиль потенциальной энергии исследованных реакций, однако траектория движения реагентов, которая проходит по дну долины на поверхности потенциальной энергии, при этом остается практически неизменной. Аналогичные результаты были получены в работах [128, 129], выполненных методом МПДП/Н с использованием приближения супермолекулы для расчета гидратации. Приблизительно такая же форма профиля потенциальной энергии для этих реакций получена и в работе [111], в которой расчеты проводились неэмпирическим методом в большом гауссовом базисе и методом Монте- Карло с атом-атомными потенциалами. Влияние сольватации на траекторию движения реагентов в последней работе не рассматривалось.
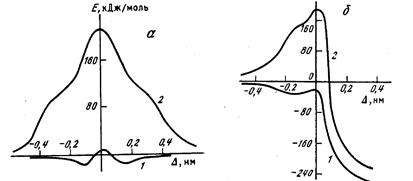
Рис. 2.4. Сечение ППЭ для реакций (IV) (a) и (V) (б)
1 – в газовой фазе; 2 – в водном растворе. Δ = R1 – R 2; R1 – расстояние между атомом углерода и уходящим атомом хлора (брома); R2 – расстояние между атомом углерода и атакующим атомом хлора (брома).
Таблица 2.3
Дата добавления: 2020-12-11; просмотров: 587;











