Вращательное движение Угловое перемещение. Угловая скорость и угловое ускорение.
Вращательным называется движение, при котором все точки тела описывают окружности с центрами на одной прямой, называемой осью вращения (рис. 6).
Поскольку каждая точка тела находится на разном удалении от оси вращения, то их скорости будут различаться. Что не совсем удобно для рассмотрения движения, поэтому в качестве кинематической характеристики вращательного движения используют угол поворота радиуса вращения данной точки тела 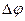 (рис. 7).
(рис. 7).
А вот углы поворота – равны (  )! Что делает угол
)! Что делает угол 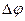 удобной для рассмотрения характеристикой.
удобной для рассмотрения характеристикой.
Быстроту вращения характеризует угловая скорость  .
.
Средней угловой скоростью называют величину, равную отношению угла поворота радиус-вектора ко времени, за которое этот поворот произошёл:
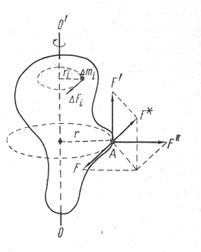
 .
.
Устремив эту дробь к пределу при 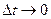 , получим мгновенное значение угловой скорости
, получим мгновенное значение угловой скорости
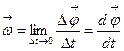 .
.
Т.е. численно угловая скорость определяется первой производной угла поворота по времени. Направление угловой скорости определяется по правилу буравчика, или правого винта (рис. 8). Вектор 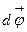 направлен так же, как и вектор
направлен так же, как и вектор 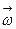 и равен по модулю углу
и равен по модулю углу 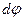 .
.
Еще одно выражение для угловой скорости можно получить из следующих соображений.
За 1 оборот 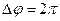 , а время одного оборота равно периоду
, а время одного оборота равно периоду
Рис. 7 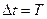 .
.
Тогда 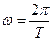 . Величина, равная
. Величина, равная 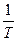 называется частотой вращения. С учетом этого получаем
называется частотой вращения. С учетом этого получаем

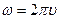 .
.
Быстроту изменения угловой скорости характеризует угловое ускорение 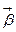 .
.
Среднее угловое ускорение – это величина, численно равная отношению изменения угловой скорости ко времени, за которое это изменение произошло
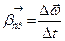 . Рис. 8
. Рис. 8
Предел данного отношения при 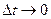 представляет собой мгновенное угловое ускорение
представляет собой мгновенное угловое ускорение
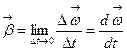 .
.
Дата добавления: 2017-01-16; просмотров: 2850;











