Четность, нечетность функций
Определение: Функция 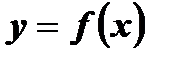 называется четной, если она обладает следующими свойствами:
называется четной, если она обладает следующими свойствами:
1) область определения этой функции симметрична относительно начала координат, то есть 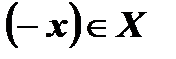 для любого
для любого 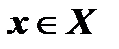 ;
;
2) для любого значения х, принадлежащего области определения этой функции, выполняется равенство 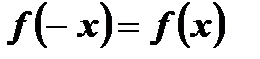 .
.
Вывод:
1. Если точка 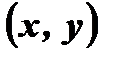 принадлежит графику четной функции, то точка
принадлежит графику четной функции, то точка 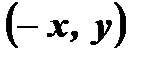 так же принадлежит графику этой функции.
так же принадлежит графику этой функции.
2.
| у |
| х |
| - 1 |
| - 2 |
| О |
| у |
| х |
| х |
| - х |
| у |
| О |
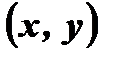 и
и 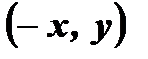 , принадлежащих графику четной функции, симметрична относительно оси ординат, следовательно, график любой четной функции симметричен относительно оси ординат (Рис. 1).
, принадлежащих графику четной функции, симметрична относительно оси ординат, следовательно, график любой четной функции симметричен относительно оси ординат (Рис. 1).
Рис. 1. Рис. 2.
Пример: 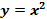 – четная функция, так как, во-первых, область определения этой функции
– четная функция, так как, во-первых, область определения этой функции 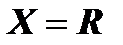 симметрична относительно начала координат; во-вторых, для любого
симметрична относительно начала координат; во-вторых, для любого 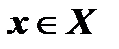 выполняется равенство
выполняется равенство 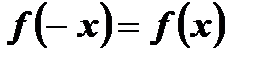 .
.
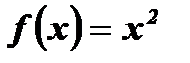 ,
, 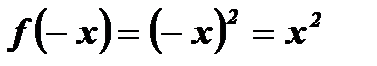 (Рис. 2).
(Рис. 2).
Определение: Функция 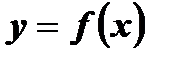 называется нечетной, если она обладает следующими свойствами:
называется нечетной, если она обладает следующими свойствами:
1) область определения этой функции симметрична относительно начала координат, то есть 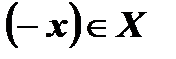 для любого
для любого 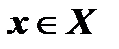 ;
;
2)
| у |
| х |
| х |
| - х |
| у |
| О |
| - у |
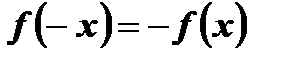 .
.
Вывод:
1. Если точка 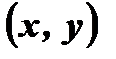 принадлежит графику нечетной функции, то точка
принадлежит графику нечетной функции, то точка 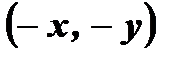 так же принадлежит графику этой функции.
так же принадлежит графику этой функции.
2. Так как любая пара точек 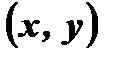 и
и 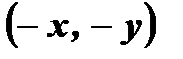 , принадлежащих графику нечетной функции, симметрична относительно начала координат, следовательно, график любой нечетной функции симметричен относительно начала координат.
, принадлежащих графику нечетной функции, симметрична относительно начала координат, следовательно, график любой нечетной функции симметричен относительно начала координат.
Пример: 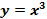 – нечетная функция, так как, во-первых, область определения этой функции
– нечетная функция, так как, во-первых, область определения этой функции 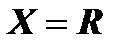 симметрична относительно начала координат; во-вторых, для любого
симметрична относительно начала координат; во-вторых, для любого 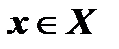 выполняется равенство
выполняется равенство 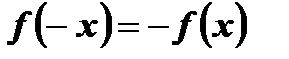 .
.
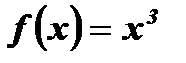 ,
, 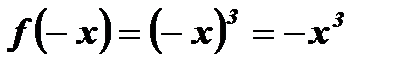 .
.
Пример: Исследовать на четность и нечетность функции:
1) 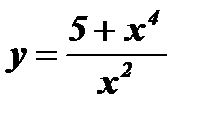 ;
;
Область определения данной функции 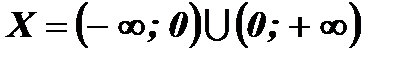 симметрична относительно начала координат. Найдем
симметрична относительно начала координат. Найдем 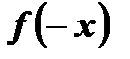 и сравним с
и сравним с 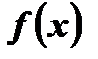 :
: 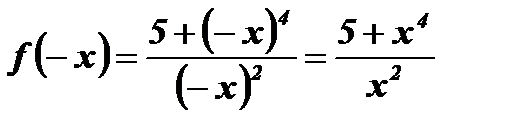 ,
, 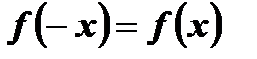 .
.
Следовательно, 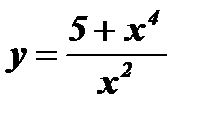 является четной функцией.
является четной функцией.
2) 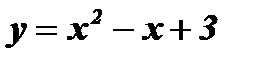 ;
;
Область определения данной функции 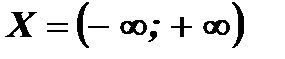 симметрична относительно начала координат. Найдем
симметрична относительно начала координат. Найдем 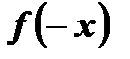 и сравним с
и сравним с 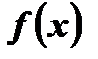 :
:
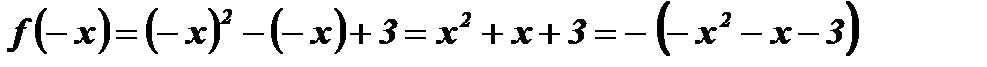 ,
,
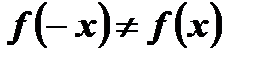 и
и 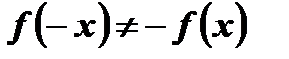 . Следовательно,
. Следовательно, 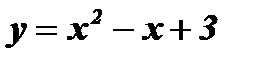 не является ни четной, ни нечетной функцией.
не является ни четной, ни нечетной функцией.
3) 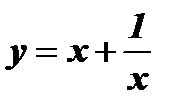 .
.
Область определения данной функции 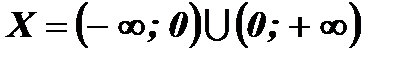 симметрична относительно начала координат. Найдем
симметрична относительно начала координат. Найдем 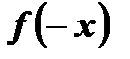 и сравним с
и сравним с 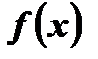 :
: 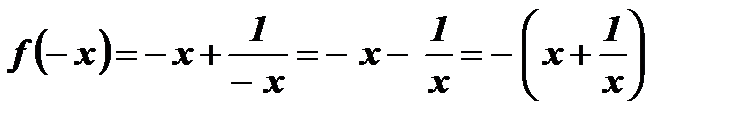 ,
, 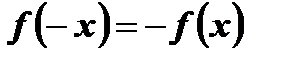 .
.
Следовательно, 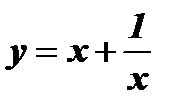 является нечетной функцией.
является нечетной функцией.
Дата добавления: 2016-09-06; просмотров: 4118;











