Обратимость функций
Определение: Функция называется обратимой (имеет обратную функцию), если она принимает каждое свое значение один раз.
Рис. 1: 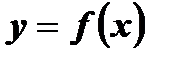 Рис. 2:
Рис. 2: 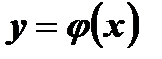
Функции 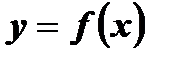 (Рис. 1)и
(Рис. 1)и 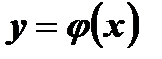 (Рис. 2) определены на
(Рис. 2) определены на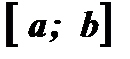 и имеют множество значений
и имеют множество значений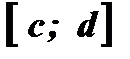 .
.
Функция 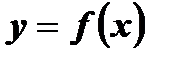 принимает каждое свое значение один раз, то естьу = f ( х ) -обратимая функция.
принимает каждое свое значение один раз, то естьу = f ( х ) -обратимая функция.
Функция 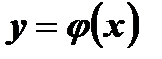 принимает некоторые свои значения не один раз, то есть у = j ( х )-необратимая функция.
принимает некоторые свои значения не один раз, то есть у = j ( х )-необратимая функция.
Вывод: Обратима только монотонная функция.
Пример: Найти функцию обратную функции 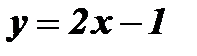 . Построить графики взаимно обратных функций.
. Построить графики взаимно обратных функций.
Решение:
1. Из формулы 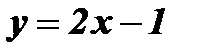 выразим х через у:
выразим х через у: 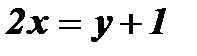 ;
; 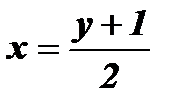 ;
; 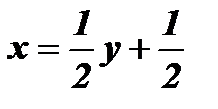 .
.
В полученной формуле поменяем местами х и у: 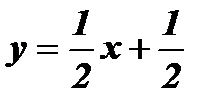 .
.
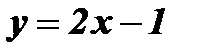 и
и 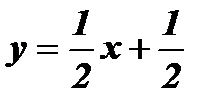 - взаимно обратные функции.
- взаимно обратные функции.
2.
Построим графики взаимно обратных функций 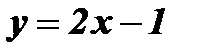 и
и 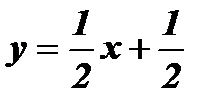 :
:
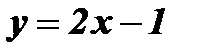 х - 2 2
х - 2 2
у - 5 3
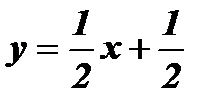
х - 5 3
у - 2 2
График функции 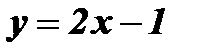 - прямая l1 проходит через точки (- 2; - 5) и (2;3).
- прямая l1 проходит через точки (- 2; - 5) и (2;3).
График функции 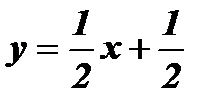 - прямая l2 проходит через точки (- 5; - 2) и (3;2).
- прямая l2 проходит через точки (- 5; - 2) и (3;2).
Прямая 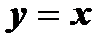 является осью симметрии прямых l1 и l2 .
является осью симметрии прямых l1 и l2 .
Вывод:
1.Чтобы получить функцию, обратную даннойфункции 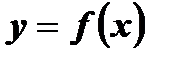 ,надо из формулы
,надо из формулы 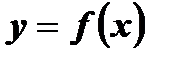 выразить х черезуи в полученной формуле поменять местами х иу.
выразить х черезуи в полученной формуле поменять местами х иу.
2.Графики взаимно обратных функций симметричны относительно прямой 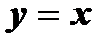 .
.
Дата добавления: 2016-09-06; просмотров: 3954;
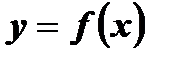 Рис. 2:
Рис. 2: 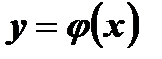
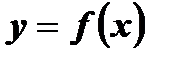 (Рис. 1)и
(Рис. 1)и 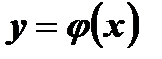 (Рис. 2) определены на
(Рис. 2) определены на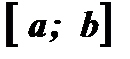 и имеют множество значений
и имеют множество значений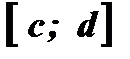 .
.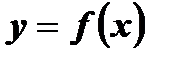 принимает каждое свое значение один раз, то естьу = f ( х ) -обратимая функция.
принимает каждое свое значение один раз, то естьу = f ( х ) -обратимая функция.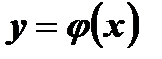 принимает некоторые свои значения не один раз, то есть у = j ( х )-необратимая функция.
принимает некоторые свои значения не один раз, то есть у = j ( х )-необратимая функция.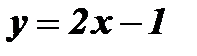 . Построить графики взаимно обратных функций.
. Построить графики взаимно обратных функций.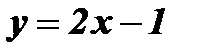 выразим х через у:
выразим х через у: 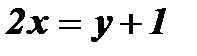 ;
; 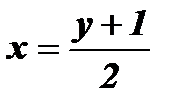 ;
; 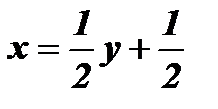 .
.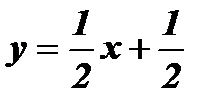 .
.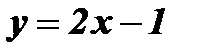 и
и 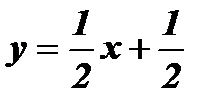 - взаимно обратные функции.
- взаимно обратные функции.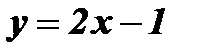 и
и 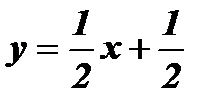 :
:
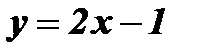 х - 2 2
х - 2 2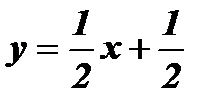
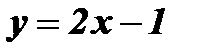 - прямая l1 проходит через точки (- 2; - 5) и (2;3).
- прямая l1 проходит через точки (- 2; - 5) и (2;3).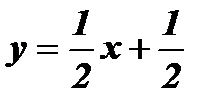 - прямая l2 проходит через точки (- 5; - 2) и (3;2).
- прямая l2 проходит через точки (- 5; - 2) и (3;2).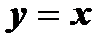 является осью симметрии прямых l1 и l2 .
является осью симметрии прямых l1 и l2 .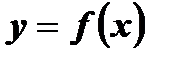 ,надо из формулы
,надо из формулы 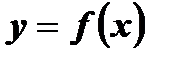 выразить х черезуи в полученной формуле поменять местами х иу.
выразить х черезуи в полученной формуле поменять местами х иу.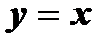 .
.










