Способы задания функции
Замечание: Функция считается заданной, если известна область определения функции и указано правило, по которому для каждого значения аргумента из области определения можно найти соответствующее значение функции.
1. Табличный способ: значения аргумента и соответствующие значения функции записаны в виде таблицы.
Достоинства: простой способ.
Недостатки: не дает полного представления о функции; не является наглядным.
Замечание: В результате экспериментального изучения какого-нибудь явления или процесса (испытание самолетов, моторов, урожайности семян) всегда устанавливается функциональная зависимость между переменными в виде таблицы.
2. Графический способ:функция задана с помощью графика.
Определение: Графиком функции называется множество точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты – соответствующим значениям функции.
Достоинства: наглядный способ.
Недостатки: небольшая точность при определении значений функции при данных значениях аргумента; ограниченность промежутка, на котором может быть построен график функции.
Замечание: Иногда табличный и графический способы задания функции являются единственно возможными, в других случаях используются как дополнительные. Метеорологи составляют таблицы выпавших осадков.В медицине о работе сердца судят по кардиограмме, которую создает прибор – кардиограф; вибратор регистрирует колебания различных сооружений (мостов, судов, зданий).
3. Аналитический способ:функция задана с помощью формулы 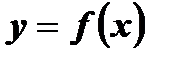 , где
, где
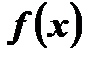 –выражение с переменной х.
–выражение с переменной х.
Достоинства: значения функции могут быть вычислены для любого значения аргумента из области определения функции.
Недостатки: не является наглядным.
Замечание:
1. Для аналитически заданной функции иногда не задают область определения явно. В таком случае область определения функции 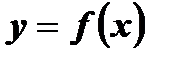 совпадает с областью определения выражения
совпадает с областью определения выражения  .
.
2. Одной и той же формулой можно задать различные функции, изменяя область определения.
3. Функция может быть задана различными формулами на различных промежутках области определения.
Пример:
1. Если функция задана формулой 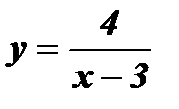 без указания области ее определения, то предполагается, что область определения этой функции – множество всех действительных чисел, кроме числа 3 (при х = 3 выражение
без указания области ее определения, то предполагается, что область определения этой функции – множество всех действительных чисел, кроме числа 3 (при х = 3 выражение 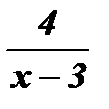 не имеет смысла ).
не имеет смысла ).
2. Различными функциями являются 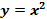 , х Î R , и
, х Î R , и 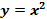 , х Î N .
, х Î N .
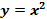 , х Î R , – квадратичная функция;
, х Î R , – квадратичная функция;
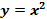 , х Î N , – числовая последовательность вида 1; 4; 9; 16;…; п2;… .
, х Î N , – числовая последовательность вида 1; 4; 9; 16;…; п2;… .
3. 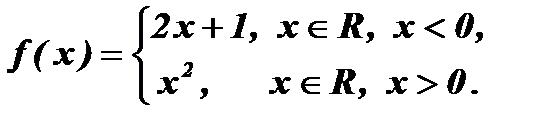
4. 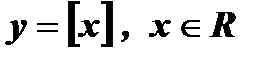 .
. 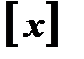 – целая часть числа х, то есть наибольшее целое число, не превосходящее х.
– целая часть числа х, то есть наибольшее целое число, не превосходящее х. 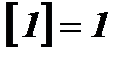 ;
; 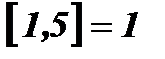 ;
; 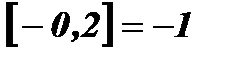 ;
; 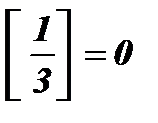 .
.
4. Словесное описание:если формулу, задающую функцию, записать сложно или невозможно, пользуются словесным описанием способа, задающего функцию.
Пример: Функция Дирихле:
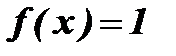 , если х – рационально;
, если х – рационально; 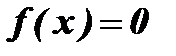 , если х – иррационально.
, если х – иррационально.
Упражнения:
- Найти область определения функции:
а) 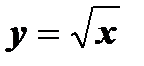 ; б)
; б) 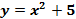 ; в)
; в) 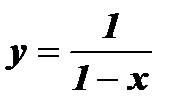 ; г)
; г) 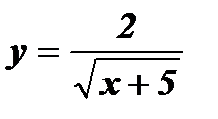 ;
;
д) 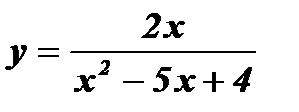 ; е)
; е) 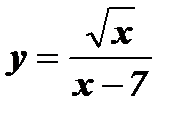 ; ж)
; ж) 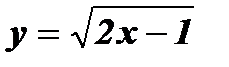 ; з)
; з) 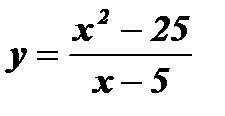 .
.
- Дана функция
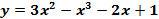 . Найти
. Найти 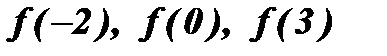 .
.
3. Свойства числовых функций
Дата добавления: 2016-09-06; просмотров: 3364;











