Любая степень положительного числа есть число положительное.

<12 3 4 5 6 7 >

Функции, их свойства и графики. Степенная функция

Степени. Корни.

Определения степеней:

1. a ⁿ= a ×a × …×a, n Î N.

2. a¹= a

3. а ⁰= 1 , 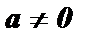(0 ⁰- не имеет смысла).

4. , .

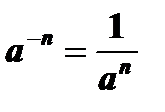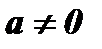5. 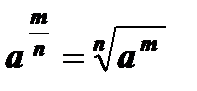, a ³ 0, n Î N, т Î Z.

Свойства степеней:

Четная степень отрицательного числа есть число положительное.

Нечетная степень отрицательного числа есть число отрицательное.

Любая степень положительного числа есть число положительное.

4. 0 ⁿ= 0, nÎ N .

5. 1 ⁿ = 1 , nÎ N .

6. .

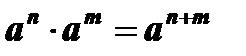7. .

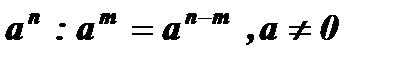8. .

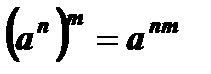9. .

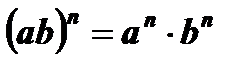10. .

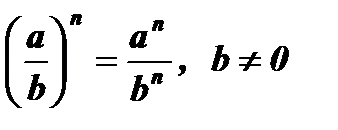Определения корней:

1. .

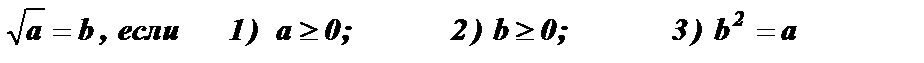2.

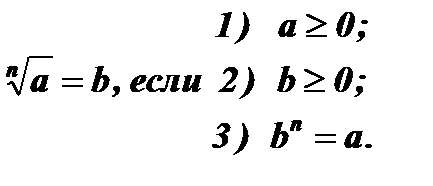
Свойства корней:

1. 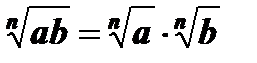, а ³ 0, b ³ 0.

2. 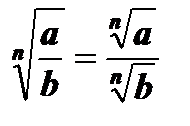, а ³ 0, b > 0.

3. 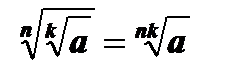, а ³ 0, nÎ N, kÎ N.

4. 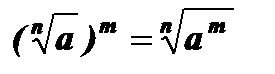, а ³ 0, nÎ N, тÎ N.

5. 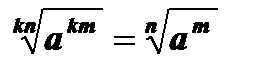, а ³ 0, nÎ N, тÎ N , kÎ N.

6. При любом значении а .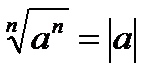

2. Числовая функция: область определения, множество значений, способы задания

Применение математики к изучению законов природы и к использованию их в технике заставило ввести в математику понятия постоянной и переменной величин. Все величины, изучаемые в математике, делятся на постоянные и переменные.

Определение: Величина называется постоянной, если она в условиях данного эксперимента сохраняет одно и то же значение.

(Постоянная – const. (лат.))

Пример: Постоянными величинами являются:

1. длина радиуса данной окружности;

<12 3 4 5 6 7 >

Дата добавления: 2016-09-06; просмотров: 1851;