Свойства взаимности

Пусть в произвольной электрической цепи единственный источник напряжения с ЭДС 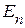действует ветви с сопротивлением 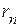в направлении от узла 1^/ к узлу 1 и в ветви с сопротивлением 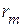создает ток 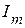, направленный от узла 2 к узлу 2^/ (рис. 2.58 а). Тогда этот же источник, будучи переключенным в ветвь с сопротивлением 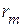и действуя в направлении от узла 2 к узлу 2^/ в ветви с сопротивлением 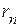, создаст ток 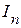, направленный от узла 1^/ к узлу 1, равный 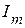(рис. 2.58 б).

Рисунок 2.58 – Пассивный четырехполюсник

Доказательство теоремы о взаимности вытекает из принципа наложения. Частичные токи равны:

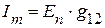— для схемы, приведенной на рисунке 2.58 а, 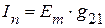— для схемы, приведенной на рисунке 2.58 б.

Так как взаимные проводимости в линейной цепи равны ( 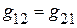), то соответственно равны токи в обеих схемах.

Пример 2.19.Применим принцип взаимности к электрической цепи, рассмотренной в примере 2.18 и приведенной на рисунке 2.55, состоящей из источника напряжения ЭДС которого равна 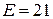В и рассчитанного тока в шестой ветви, равного 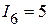мА. С этой целью, перенесем источник напряжения с ЭДС равной 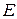в шестую ветвь. С целью проверки свойства взаимности, рассчитаем ток 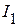во вновь полученной схеме, приведенной на рисунке 2.59.

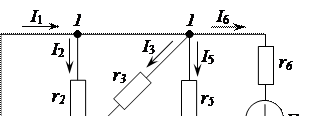
Рисунок 2.59 – Расчетная схема электрической цепи

1. Определяем параметры исходной схемы.

1.1. Определяем входное сопротивление всей цепи. Оно соответственно равно

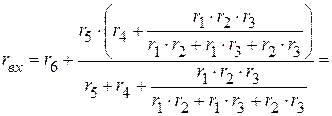
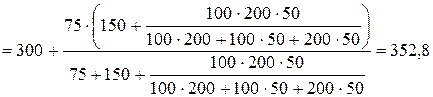Ом.

1.2. Определяем токи в ветвях. С этой целью используем закон Ома.

1.2.1. Ток 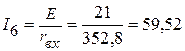мА.

1.2.2. Определяем ток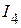и и 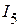. Для их определения необходимо предварительно определить напряжение .

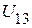1.2.2.1. Из приведенной схемы, следует

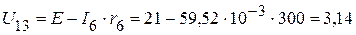В.

1.2.2.2. Тогда токи в ветвях:

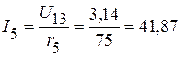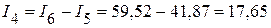мА;

мА.

1.2.3. Определяем ток 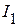. Для его определения необходимо предварительно определить напряжение .

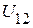1.2.3.1. Из приведенной схемы, следует

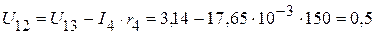В.

1.2.3.2. Тогда ток 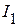равен:

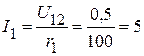мА.

Таким образом, величина тока 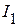, рассчитанная в эквивалентной схеме (рис. 2.59), численно равна величине тока 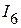, рассчитанной в исходной схеме (рис. 2.55), что подтверждает свойство взаимности.