Входные и взаимные проводимости ветвей

Используя принцип наложения, можно записать уравнение, для нахождения тока в произвольной ветви линейной электрической цепи, например в ветви 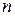, в виде

.

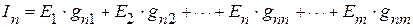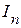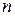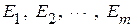В приведенном уравнении, ток обозначает ток в ветви , а - ЭДС соответветсвенно в первой, второй и 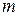– ой ветвях.

Каждый из множителей, в приведенном уравнении, с двумя одинаковыми индексами 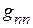называют входной проводимостью ветви 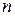, а с двумя различными индексами 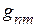называют взаимной проводимостью ветве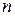й и .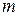

Численные значения входных и взаимных проводимостей ветвей определяются следующим путем. Приравниваем в произвольной рассматриваемой схеме все источники напряжения к нулю, кроме 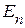. Тогда, из приведенного уравнения, для нахождения тока в произвольной ветви электрической цепи, ток в 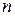– ой равен

.

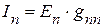Откуда .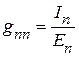

Следовательно, входная проводимость произвольной ветви электрической схемы, определяется отношением величины тока 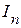к ЭДС источника напряжения 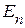в этой при равных нулю ЭДС источников напряжения в остальных ветвях схемы.

Источник напряжение с ЭДС 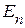, включенный в ветвь 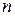, вызывает токи во всех ветвях произвольной линейной электрической цепи. Величина тока в 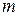– ой ветви определяется из уравнения

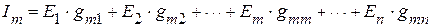
при равных нулю всех ЭДС, кроме 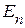, т.е.

.

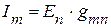Откуда .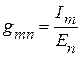

Таким образом, взаимная проводимость двух произвольных ветвей электрической цепи, определяется отношением тока 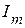в одной ветви к ЭДС 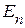в другой ветви при равных нулю ЭДС источников напряжения в остальных ветвях схемы.

Из свойства взаимности следует равенство .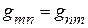

Входные и взаимные проводимости можно рассчитать или определить экспериментально.

Пример 2.20. Определение входных и взаимных проводимостей ветвей расчетным путем покажем на примере электрической цепи, рассмотренной в примере 2.15.

Из примера 2.15 , частичные токи от действия источника напряжения 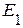=20 В:

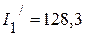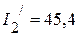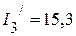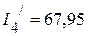мА, мА, мА,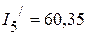

мА, мА.

Частичные токи от действия источника напряжения 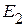=15 В:

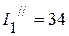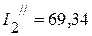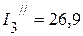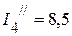мА, мА, мА,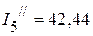

мА, мА.

1. Входная проводимость 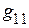первой ветви равна отношению тока 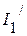к ЭДС :

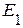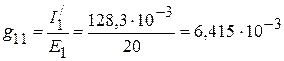См.

2. Взаимные проводимости между первой и остальными ветвями:

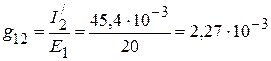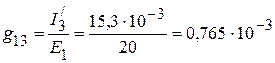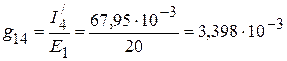См,

См,

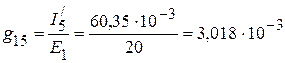См,

См.

3. Входная проводимость 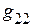первой ветви равна отношению тока 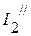к ЭДС :

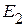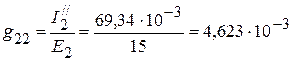См.

4. Взаимные проводимости между второй и остальными ветвями:

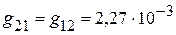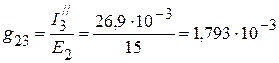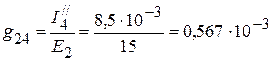См,

См,

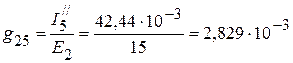См,

См.

5. Используя принцип наложения, записываем уравнения, для нахождения токов в ветвях:

=

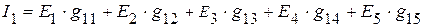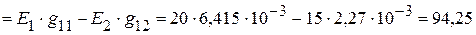мА,

=

мА,

=

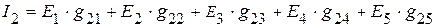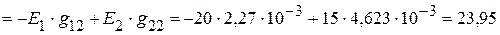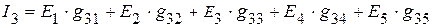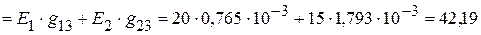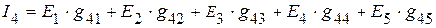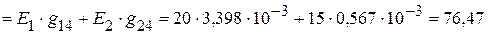мА,

=

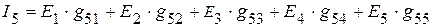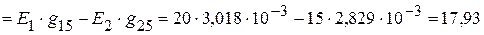мА,

=

мА.

Токи в ветвях, рассчитанные в примерах 2.2 и 2.20, совпадают.