Метод эквивалентного генератора
Метод применяют в том случае, если необходимо определить ток в одной ветви разветвлённой схемы.
Идея метода.
1. Выделяется ветвь с сопротивлением, в которой необходимо определить ток 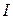 . Остальную часть схемы представляют в виде активного двухполюсника, представленного на рисунке 2.43 а.
. Остальную часть схемы представляют в виде активного двухполюсника, представленного на рисунке 2.43 а.
2. Активный двухполюсник заменяют эквивалентным источником питания (генератором). В результате получим простую одноконтурную схему, представленную на рисунке 2.43 б. Ток в полученой схеме равен
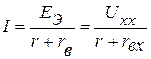 ,
,
где 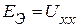 - напряжению холостого хода активного двухполюсника (рис. 2.43 в),
- напряжению холостого хода активного двухполюсника (рис. 2.43 в),
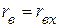 – входное сопротивление пассивного двухполюсника.
– входное сопротивление пассивного двухполюсника.
Внутреннее сопротивление источника 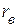 равно входному сопротивлению пассивного двухполюсника
равно входному сопротивлению пассивного двухполюсника 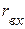 , полученного из активного двухполюсника, путём изъятия из схемы источников питания и замены их внутренними сопротивлениями (рис. 2.43,г).
, полученного из активного двухполюсника, путём изъятия из схемы источников питания и замены их внутренними сопротивлениями (рис. 2.43,г).

Рисунок 2.43 – Идея метода эквивалентного генератора
Рассмотрим справедливость вышеуказанного.
1. В исходной схеме выделяем ветвь с сопротивлением 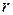 , в которой необходимо определить ток
, в которой необходимо определить ток 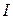 . Остальную часть схемы представляем в виде активного двухполюсника
. Остальную часть схемы представляем в виде активного двухполюсника 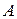 (рис. 2.44 а).
(рис. 2.44 а).

Рисунок 2.44 – Доказательство метода эквивалентного генератора
2. Осуществляем разрыв выделенной ветви (рис. 2.44 б). В полученной схеме ток 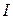 равен нулю. Напряжение на зажимах равно напряжению холостого хода
равен нулю. Напряжение на зажимах равно напряжению холостого хода 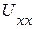 .
.
3. В разрыв включаем источник напряжения 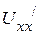 , величина которого равна напряжению холостого хода
, величина которого равна напряжению холостого хода 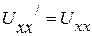 . (рис. 2.44 в). Ток в выделенной ветви также равен нулю.
. (рис. 2.44 в). Ток в выделенной ветви также равен нулю.
4. Последовательно с источником напряжения 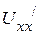 , включаем ещё один источник напряжения
, включаем ещё один источник напряжения 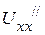 , направленный навстречу, величина ЭДС которого равна
, направленный навстречу, величина ЭДС которого равна 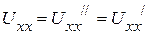 (рис. 2.44 г). В результате они компенсируют друг - друга, поэтому ток в выделенной ветви
(рис. 2.44 г). В результате они компенсируют друг - друга, поэтому ток в выделенной ветви 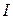 равен току в исходной схеме (рис.2.44 д).
равен току в исходной схеме (рис.2.44 д).
5. К полученной схеме (рис. 2.44 г) применяем метод наложения.
Алгебраическая сумма частичных токов активного двухполюсника и первого источника равна нулю (рис. 2.44 д), следовательно, ток в исходной схеме равен частичному току от добавленного источника напряжения 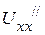 (рис. 2.44 г). Ток в полученной схеме равен
(рис. 2.44 г). Ток в полученной схеме равен
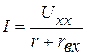 ,
,
где 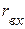 – входное сопротивление пассивного двухполюсника, полученного из активного двухполюсника.
– входное сопротивление пассивного двухполюсника, полученного из активного двухполюсника.
Основные этапы рассмотрим на примере расчета тока 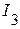 в электрической цепи, представленной на рисунке 2.45.
в электрической цепи, представленной на рисунке 2.45.

Рисунок 2.45 – Электрическая цепь
1. Определяем 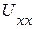 .
.
1.1. Удаляем 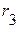 из схемы и вычерчиваем схему активного двухполюсника (рис. 2.45).
из схемы и вычерчиваем схему активного двухполюсника (рис. 2.45).

Рисунок 2.45 – Схема активного двухполюсника
1.2. Определяем токи в схеме двухполюсника:
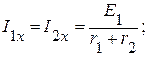
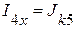 .
.
1.3. Определяем 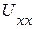 . Согласно второго закона Кирхгофа имеем:
. Согласно второго закона Кирхгофа имеем:
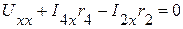 =>
=> 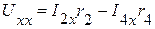 .
.
2.Определяем входное сопротивление.
2.1. Из схемы активного двухполюсника удаляем источники питания и заменяем их внутренними сопротивлениями. В результате схема пассивного двухполюсника имеет вид, представленный на рисунке 2.46.

Рисунок 2.46 – Схема пассивного двухполюсника
2.2. Входное сопротивление соответственно равно:
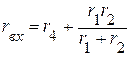 .
.
3. Ток 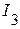 в схеме (рис. 2.45) равен:
в схеме (рис. 2.45) равен:
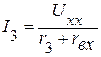 .
.
Пример 2.16. Рассмотрим рекомендованный порядок расчета на конкретном примере электрической цепи, рассмотренной в примере 2.14 и представленной на рисунке 2.48, для определения тока 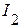 . Принимаем E1 = 50 B, Е5 = 60 В, Jk4 = 5 А, r1 = 10 Ом, r2 = 8 Ом, r3= 15 Ом, r4 = 20 Ом.
. Принимаем E1 = 50 B, Е5 = 60 В, Jk4 = 5 А, r1 = 10 Ом, r2 = 8 Ом, r3= 15 Ом, r4 = 20 Ом.
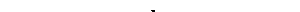
Рисунок 2-48 - Схема электрической цепи
1. Определяем напряжение холостого хода 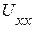 .
.
1.1. Удаляем из исходной схемы сопротивление 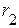 и вычерчиваем схему активного двухполюсника (рис. 2.49).
и вычерчиваем схему активного двухполюсника (рис. 2.49).
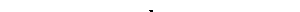
Рисунок 2.49 - Схема активного двухполюсника
1.2. Определяем токи в схеме активного двухполюсника:
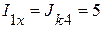 А,
А, 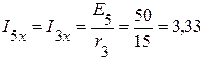 А.
А.
1.3. Определяем Uxx по второму закону Кирхгофа:
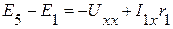 ,
, 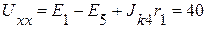 B.
B.
2. Определяем входное сопротивление пассивного двухполюсника.
2.1. Удаляем источники питания и вычерчиваем схему пассивного двухполюсника (рис. 2.50).
Рисунок 2.50 - Схема пассивного двухполюсника
2.2. Определяем входное сопротивление: 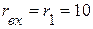 Ом.
Ом.
3. Определяем ток 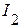 :
: 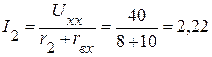 А.
А.
Величина тока 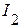 , рассчитанная в примерах 2.14 и 2.16, совпадает.
, рассчитанная в примерах 2.14 и 2.16, совпадает.
Пример 2.17.Определим ток 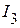 методом эквивалентного генератора для электрической цепи, рассмотренной в примере 2.2.
методом эквивалентного генератора для электрической цепи, рассмотренной в примере 2.2.
1. Определяем напряжение холостого хода 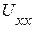 .
.
1.1. Удаляем из исходной схемы сопротивление 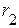 и вычерчиваем схему активного двухполюсника (рис. 2.51).
и вычерчиваем схему активного двухполюсника (рис. 2.51).

Рисунок 2.51 - Схема активного двухполюсника
1.2. Определяем токи в схеме активного двухполюсника (рис. 2.52), используя метод узловых потенциалов.

Рисунок 2.52 – Схема активного двухполюсника
1.2.1 Осуществляем предварительный анализ схемы. Количество ветвей – 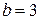 , количество узлов –
, количество узлов – 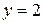 .
.
Потенциал первого узла принимаем равным нулю: 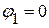 . Следовательно, необходимо определить потенциал
. Следовательно, необходимо определить потенциал 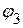 .
.
1.2.2. Составляем уравнение для определения потенциала 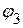 :
:
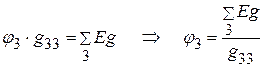 .
.
1.2.2.1. Подставляем числовые значения и находим потенциал 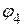 .
.
1.2.2.2. Сумма проводимостей ветвей, подключенных к соответствующим узлам:
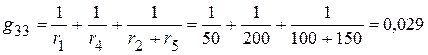 См;
См;
Узловые токи
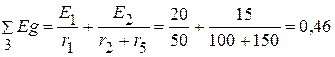 А.
А.
1.2.2.3. После подстановки цифровых значений, определяем потенциал 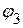 :
: 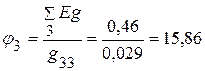 В.
В.
1.2.3. Определяем токи в ветвях электрической цепи, приведенной на рисунке 2.51.
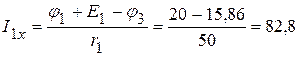 мА,
мА,
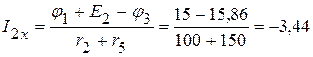 мА,
мА,
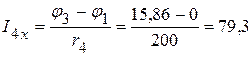 мА.
мА.
1.3. Определяем 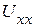 по второму закону Кирхгофа (рис. 2.51):
по второму закону Кирхгофа (рис. 2.51):
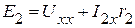
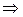
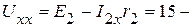
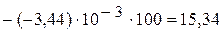 B.
B.
2. Определяем входное сопротивление пассивного двухполюсника.
2.1. Удаляем источники питания и вычерчиваем схему пассивного двухполюсника (рис. 2.53).

Рисунок 2.53 - Схема пассивного двухполюсника
2.2. Определяем входное сопротивление:
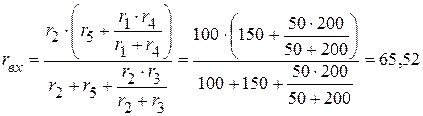 Ом.
Ом.
3. Определяем ток 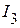 :
: 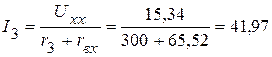 мА.
мА.
Величина тока 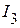 , рассчитанная в примерах 2.2 и 2.17, совпадает.
, рассчитанная в примерах 2.2 и 2.17, совпадает.
Дата добавления: 2016-08-23; просмотров: 2665;











