Активный трехполюсник. Рассмотрим основные свойства активных трехполюсников
Рассмотрим основные свойства активных трехполюсников и методов определения параметров их схем замещения, на примере разветвленной электрической цепи, показанной на рисунке 2.66. Параметры приведенной цепи: E31 = 23,2 B, Е42 = 20 В, r14 = 300 Ом, r42 = 600 Ом, r34 = 900 Ом, r31 = 200 Ом, r12 = 150 Ом, r23 = 400 Ом, R1 = 50 Ом, R2 = 75 Ом, R3 = 100 Ом.
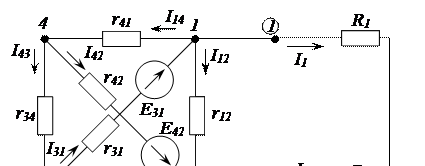
Рисунок 2.66 - Разветвленная электрическая цепь к пояснению свойств активного трехполюсника
Данная схема состоит из пяти узлов 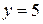 и девяти ветвей
и девяти ветвей 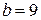 . При решении основной задачи расчета электрической цепи, например с применением законов Кирхгофа, необходимо составить и решить систему уравнений, равную количеству ветвей
. При решении основной задачи расчета электрической цепи, например с применением законов Кирхгофа, необходимо составить и решить систему уравнений, равную количеству ветвей 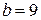 . При использовании метода контурных токов, необходимо составить и решить систему уравнений с
. При использовании метода контурных токов, необходимо составить и решить систему уравнений с 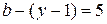 неизвестными контурными токами.При использовании метода узловых потенциалов, необходимо составить и решить систему уравнений с
неизвестными контурными токами.При использовании метода узловых потенциалов, необходимо составить и решить систему уравнений с 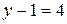 неизвестными потенциалами узлов приведенной схемы. Рассчитаем токи в ветвях приведенной схемы, с использованием свойств активных трехполюсников.
неизвестными потенциалами узлов приведенной схемы. Рассчитаем токи в ветвях приведенной схемы, с использованием свойств активных трехполюсников.
В общем случае в разветвленных цепях можно выделить звезду или треугольник, а остальную часть схемы представить в виде активного трехполюсника.
Так на схеме, приведенной на рисунке 2.66, выделены три ветви с резистивными сопротивлениями R1, R2, и R3, условно называемые нагрузкой. Остальная часть схемы может быть представлена активным трехполюсником (рис. 2.67 а). Активный трехполюсник может быть замещен эквивалентной схемой. В этом случае схема имеет вид, представленный на рисунке 2.67 б.
Приведенная схема была исследована расчетным путем и экпериментально.
Рассмотрим методы определения параметров схемы замещения активного трехполюсника 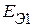 ,
, 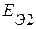 ,
, 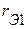 ,
, 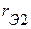 ,
, 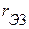 . На первом этапе используем расчетный метод.
. На первом этапе используем расчетный метод.
1. Определяем напряжения холостого хода активного трехполюсника 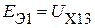 ,
, 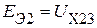 .
.
1.1. Удаляем из схемы сопротивления нагрузки R1 и R2 (разрываем ветвь) и вычерчиваем схему активного трехполюсника (2.68)
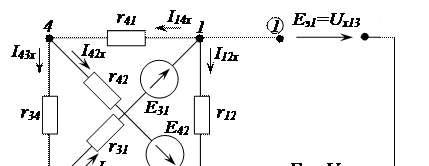
Рисунок 2.68 - Схема активного трехполюсника
1.2. Произвольным методом (МКТ, МУП и т.д.), определяем токи в схеме активного трехполюсника.
В приведенной на рисунке 2.69 схеме, для определение токов в ветвях, используем метод узловых потенциалов.
1.2.1. Осуществляем предварительный анализ схемы. Количество ветвей – 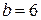 , количество узлов –
, количество узлов – 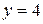 .
.
Потенциал четвертого узла принимаем равным нулю: 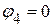 . Следовательно, необходимо определить потенциалы
. Следовательно, необходимо определить потенциалы 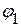 ,
, 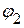 ,
, 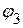 .
.
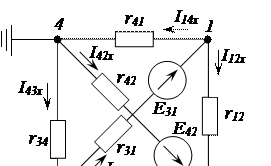
Рисунок 2.69 – Расчетная схема активного трехполюсника
1.2.2. Составляем уравнения для определения потенциалов 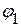 ,
, 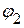 ,
, 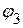 .
.
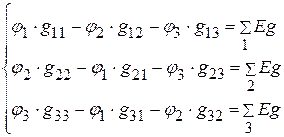 .
.
1.2.3. Подставляем числовые значения и решаем систему уравнений.
1.2.3.1. Проводимости ветвей
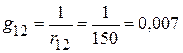 См;
См;
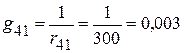 См;
См;
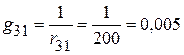 См;
См;
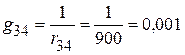 См;
См;
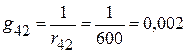 См;
См;
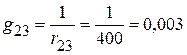 См.
См.
1.2.3.2. Сумма проводимостей ветвей, подключенных к соответствующим узлам:
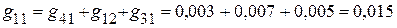 См;
См;
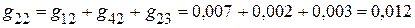 См;
См;
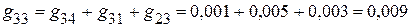 См.
См.
Сумма проводимостей, соединяющих различные узлы
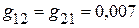 См;
См;
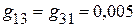 См;
См;
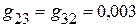 См.
См.
Узловые токи 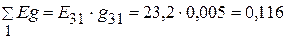 А,
А,
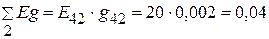 А,
А,
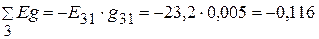 А.
А.
1.2.3.3. После подстановки цифровых данных система имеет вид
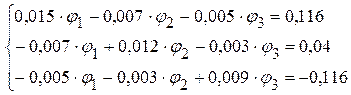
1.2.3.4. Решая данную систему уравнений произвольным методом, определяем потенциалы:
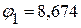 В,
В,
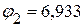 В,
В,
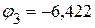 В.
В.
1.2.3.5. Определяем токи в ветвях электрической цепи, приведенной на рис. 2.69.
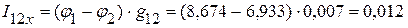 А,
А,
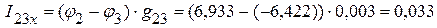 А,
А,
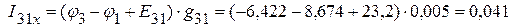 А,
А,
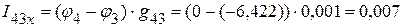 А,
А,
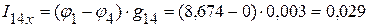 А,
А,
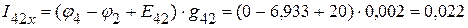 А.
А.
1.3. Используя второй закон Кирхгофа, определяем 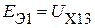 и
и 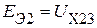 .
.
Из контура 15321 : 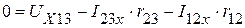
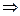
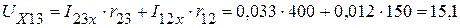 В.
В.
Из контура 5325 : 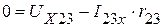
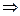
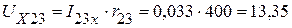 В.
В.
2. Определяем сопротивления эквивалентной схемы замещения 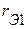 ,
, 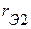 ,
, 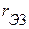 пассивного трехполюсника.
пассивного трехполюсника.
2.1. Из схемы активного трехполюсника удаляем источники питания и вычерчиваем схему пассивного трехполюсника (рис. 2.70).
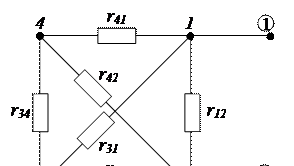
Рисунок 2-70 - Схема пассивного трехполюсника
2.1.1. Звезду из сопротивлений 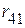 ,
, 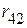 ,
, 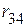 преобразовываем в треугольник сопротивлений (рис. 2.71 а).
преобразовываем в треугольник сопротивлений (рис. 2.71 а).
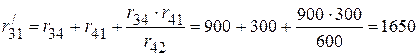 Ом;
Ом;
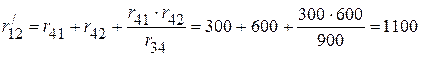 Ом;
Ом;
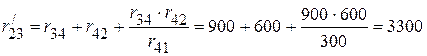 Ом.
Ом.
2.1.2. Параллельно соединенные сопротивления 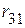 и
и 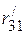 ,
, 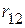 и
и 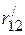 ,
, 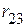 и
и 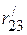 заменяем эквивалентными сопротивлениями (рис. 2.71 б).
заменяем эквивалентными сопротивлениями (рис. 2.71 б).
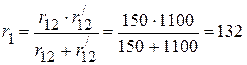 Ом;
Ом;
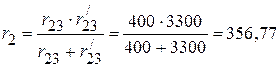 Ом;
Ом;
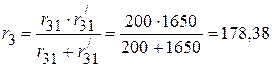 Ом.
Ом.
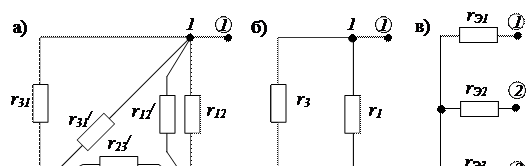
Рисунок 2.71 – Нахождение сопротивлений эквивалентной схемы замещения
Дата добавления: 2016-08-23; просмотров: 3099;











