Теоремы линейных электрических цепей

Баланс мощностей

Теорема о балансе мощностей: мощность, генерируемая источниками питания схемы, равняется мощности, потребляемой приёмниками.

Если в электрической цепи отсутствуют источники тока, то баланс мощностей имеет вид

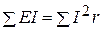где 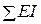– суммарная мощность, генерируемая источниками напряжения,

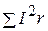– суммарная мощность, потребляемая приемниками.

Если электрические цепи содержат источники тока, то выражение баланса мощностей имеет вид

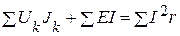где 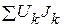– суммарная мощность генерируемая источниками тока.

Напряжение 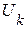определяется с помощью второго закона Кирхгофа.

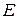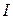Правило знаков: если в какой-либо ветви ЭДС и ток совпадают по направлению, то берется знак ”+”. Аналогично, при положительном направлени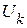и и 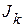берется знак ”+” (положительное направление 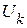направлено навстречу току источника тока ).

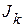Если в цепи имеется несколько источников питания, то возможно, что некоторые их них будут иметь знак ”-”. Это означает, что данный источник питания работает в режиме потребления энергии. Например, заряд аккумуляторной батареи. Однако, суммарная мощность, генерируемая источниками питания, в замкнутой электрической цепи, положительна.

Метод наложения

Токи в разветвлённых электрических цепях определяются как алгебраическая сумма токов от каждого источника в отдельности (принцип суперпозиции).

Поочерёдно рассчитываются частичные токи от действия каждого источника в отдельности. При этом остальные источники «изымаются» из схемы и вместо них «ставится» их внутреннее сопротивление («закоротка» – источник напряжения, «разрыв» – источник тока). Затем, алгебраическим суммированием токов, полученных от действия каждого источника в отдельности, находим токи в ветвях цепи.

Рассмотрим основные этапы расчета на примере электрической цепи, приведенной на рисунке 2.33.

Рисунок 2.33 – Расчетная электрическая схема

1. Осуществляем предварительный анализ.

Приведенная схема содержит два источника питания – источник напряжения с ЭДС 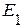и источник тока 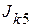, ветвей 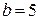, ветвей с источником тока 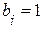, следовательно, неизвестных токов ветвях .

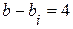2. Рассчитываем частичные токи от действия источника напряжения .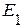

2.1. Из исходной схемы удаляем источник тока (заменяем его внутренним сопротивлением 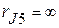). Полученная схема имеет вид, приведенный на рисунке 2.34.

Рисунок 2.34 – Схема для расчета частичных токов от действия Е₁

2.2. Определяем входное сопротивление цепи и сопротивления на участках цепи.

.

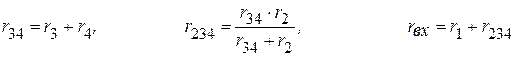2.3. Определяем частичные токи.

2.3.1. Частичный ток : .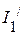

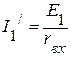2.3.2. Для определения частичных токов 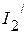, , 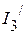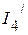необходимо определить напряжение 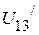на зажимах 13. Оно соответственно равно:

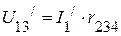или .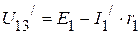

2.3.3. Частичные токи 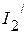, , 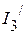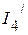соответственно равны:

, .

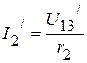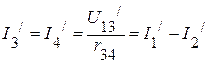3. Определяем частичные токи от действия источника тока .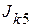

3.1. Из исходной схемы удаляем источник напряжения (заменяем его внутренним сопротивлением 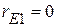). Полученная схема имеет вид, приведенный на рисунке 2.35.

Рисунок 2.35 – Схема для расчета частичных токов от действия J_k₅

3.2 Определяем входное сопротивление цеп и сопротивления на участках цепи:

.

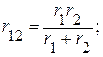
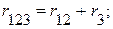
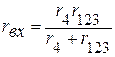3.3. Рассчитываем частичные токи в ветвях от действия источника тока .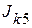

3.3.1. Напряжение на зажимах источника тока:

.

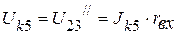3.3.2. Частичные токи: .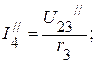

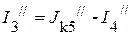3.3.3. Напряжение на зажимах 13: .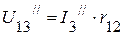

3.3.4. Частичные токи .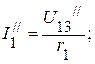

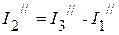4. Определяем токи в исходной схеме, как алгебраическую сумму частичных токов:

.

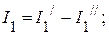
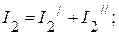
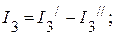
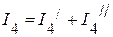Пример 2.14. Рассмотрим порядок расчета на конкретном примере элетрической цепи, приведенной на рисунке 2.36, с параметрами E₁ = 50 (B), Е₅ = 60 В, J_k₄ = 5 А, r₁ = 10 Ом, r₂ = 8 Ом, r₃= 15 Ом, r₄ = 20 Ом.

Рисунок 2.36 - Схема электрической цепи

1. Осуществляем предварительный анализ.

Приведенная схема содержит три источника питания – источник напряжения с ЭДС 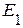, источник напряжения с ЭДС 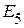, и источник тока 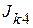, ветвей 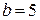, ветвей с источником тока 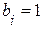, следовательно, неизвестных токов ветвях .

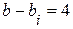2. Рассчитываем частичные токи ( 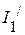, , 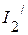, , 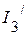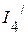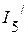) от действия источника напряжения .

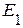2.1. Удаляем из исходной схемы источник напряжения 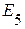и источник тока 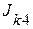и заменяем их внутренними сопротивлениями. В результате получаем схему, приведенную на рисунке 2.37.

Рисунок 2.37 - Схема для расчета частичных токов

от действия источника напряжения Е₁

2.2. Рассчитываем частичные токи.

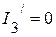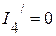2.2.1. Частичные токи А, А.

2.2.2. Частичные токи 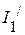, , 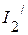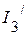соответственно равны:

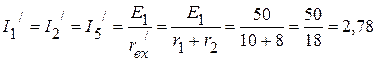А.

3. Рассчитываем частичные токи ( 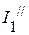, , 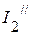, , 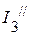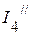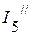) от действия источника напряжения .

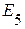3.1. Удаляем из исходной схемы источник напряжения 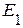и источник тока 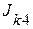и заменяем их внутренними сопротивлениями. В результате получаем схему, приведенную на рисунке 2.38.

Рисунок 2.38 - Схема для расчета частичных токов

от действия источника напряжения Е₅

3.2. Рассчитываем частичные токи.

3.2.1. Частичный ток 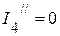А.

3.2.2. Частичные токи 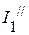, , 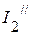, 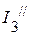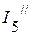соответственно равны:

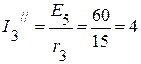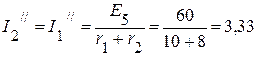А,

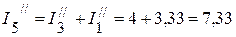А,

А.

4. Рассчитываем частичные токи ( 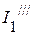, , 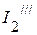, , 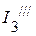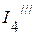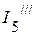) от действия источника тока .

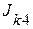4.1. Удаляем из исходной схемы источники напряжения 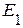и 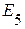и заменяем их внутренними сопротивлениями. В результате получаем схему, приведенную на рисунке 2.39.

Рисунок 2.39 - Схема для расчета частичных токов

от действия источника тока J_k₄

4.2. Рассчитываем входное сопротивление цепи относительно зажимов 13:

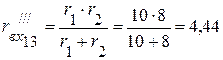Ом.

4.3. Определяем частичные токи от действия источника тока .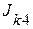

4.3.1. Для определения частичных токов 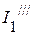, , 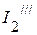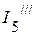необходимо определить напряжение 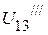. Оно соответственно равно:

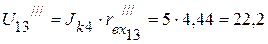B.

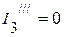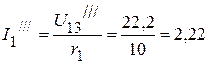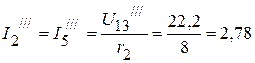4.3.2. Частичные токи: А,

А,

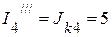А,

А.

5. Рассчитываем токи в исходной схеме:

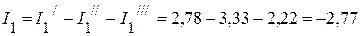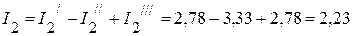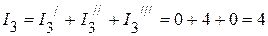А;

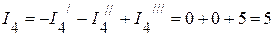А;

А;

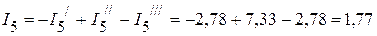А;

А.

6. Проверяем решение, составив баланс мощностей.

6.1. Мощность источников:

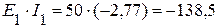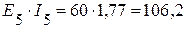Вт,

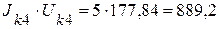Вт,

Вт,

где 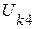– напряжение на зажимах источника тока, равное

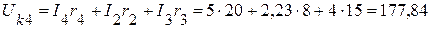B.

Знак ”-” указывает на то, что первый источник работает в режиме потребителя электроэнергии (например, зарядка аккумулятора).

Суммарная мощность источников:

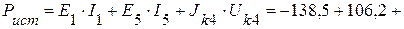
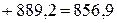Вт.

6.2. Мощность приемников:

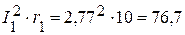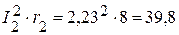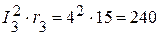Вт,

Вт,

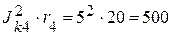Вт,

Вт.

Суммарная мощность приемников:

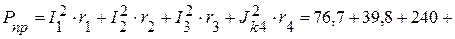
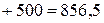Вт.

6.3. Из сравнения генерируемой мощности источниками и потребляемой мощности приемниками, следует, что погрешность вычислении 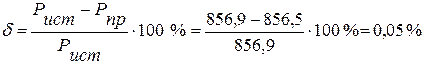и не превышает 0,5%.

Пример 2.15.Рассмотрим решение задачи, приведенной в примере 2.2, методом наложения. Электрическая цепь для рассматриваемого метода, приведена на рисунке 2.40.

1. Осуществляем предварительный анализ схемы.

Приведенная схема содержит два источника питания – источник напряжения с ЭДС 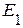и источник напряжения с ЭДС 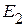, ветвей 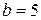, узлов .

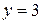Рисунок 2.40 – Электрическая цепь постоянного тока

2. Рассчитываем частичные токи ( 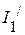, , 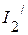, , 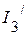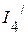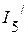) от действия источника напряжения .

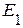2.1. Удаляем из исходной схемы источник напряжения 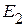и заменяем его внутренним сопротивлением. В результате получаем схему, приведенную на рисунке 2.41.

Рисунок 2.41 - Схема для расчета частичных токов

от действия источника напряжения Е₁

2.2. Рассчитываем входное сопротивление цепи относительно зажимов 34:

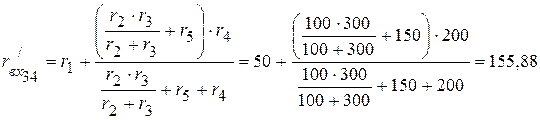Ом.

2.3. Рассчитываем частичные токи.

2.3.1. Частичный ток 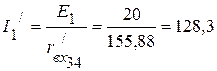мА.

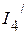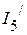2.3.2. Для определения частичных токов и , необходимо определить напряжение 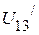. Оно соответственно равно:

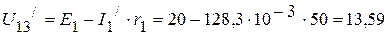B.

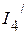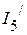2.3.3. Частичные токи и соответственно равны:

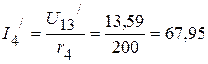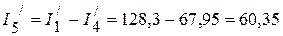мА,

мА.

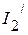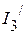2.3.4. Для определения частичных токов и , необходимо определить напряжение 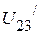. Оно соответственно равно:

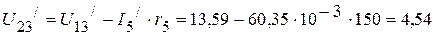B.

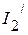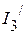2.3.5. Частичные токи и соответственно равны:

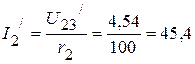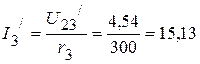мА,

мА.

3. Рассчитываем частичные токи ( 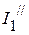, , 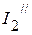, , 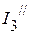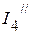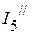) от действия источника напряжения .

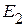3.1. Удаляем из исходной схемы источник напряжения 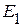и заменяем его внутренним сопротивлением. В результате получаем схему, приведенную на рисунке 2.42.

Рисунок 2.42 - Схема для расчета частичных токов

от действия источника напряжения Е₂

3.2. Рассчитываем входное сопротивление цепи относительно зажимов 35:

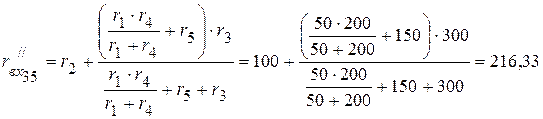Ом.

3.3. Рассчитываем частичные токи.

3.3.1. Частичный ток 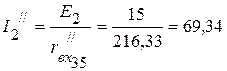мА.

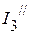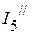3.3.2. Для определения частичных токов и , необходимо определить напряжение 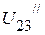. Оно соответственно равно:

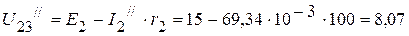B.

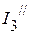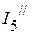3.3.3. Частичные токи и соответственно равны:

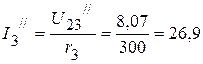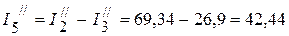мА,

мА.

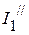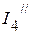3.3.4. Для определения частичных токов и , необходимо определить напряжение 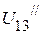. Оно соответственно равно:

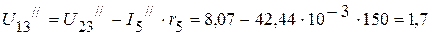B.

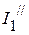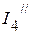3.3.5. Частичные токи и соответственно равны:

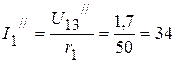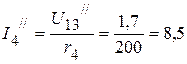мА,

мА.

4. Рассчитываем токи в исходной схеме:

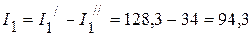мА;

мА;

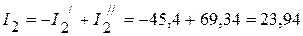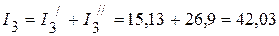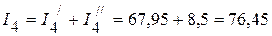мА;

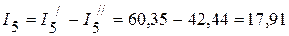мА;

мА.

Токи в ветвях, рассчитанные в примерах 2.2 и 2.15, совпадают.

<11 12 131415 16 17 >

Дата добавления: 2016-08-23; просмотров: 2335;