Расчет момента и мощности главного привода двухвалковой клети при параметрах технологического режима, не соответствующих простому процессу прокатки.
В реальной технологии редко соблюдаются одновременно все условия простого процесса прокатки.
Наиболее распространенные варианты технологии, имеющие отступления от простого процесса прокатки:
а) силы переднего и заднего натяжений полосы не равны между собой;
б) прокатка ведется не с постоянной скоростью, а с ускорением или замедлением.
Рассмотрим методику расчета мощности и момента главного привода при указанных вариантах технологии.
а) Силы переднего и заднего натяжений полосы не равны между собой
Если сила заднего натяжения То большие силы переднего натяжения Т1, то их разность 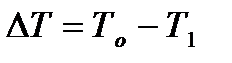 направлена назад (именно этот вариант натяжений показан на схеме рис. 10.2). В этом случае уравнение равновесия полосы (10.6) выполняется только тогда, когда силы R, действующие на полосу со стороны двух валков, отклоняются от вертикали (эти силы изображены на рис. 10.2 пунктиром), чтобы их проекции на ось Х, равные
направлена назад (именно этот вариант натяжений показан на схеме рис. 10.2). В этом случае уравнение равновесия полосы (10.6) выполняется только тогда, когда силы R, действующие на полосу со стороны двух валков, отклоняются от вертикали (эти силы изображены на рис. 10.2 пунктиром), чтобы их проекции на ось Х, равные
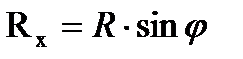 , (10.19)
, (10.19)
уравновешивали разность сил натяжений:
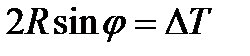 . (10.20)
. (10.20)
Из зависимостей (10.19) и (10.20) получим: 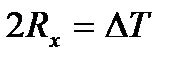 , следовательно, силы Rx, действующие на полосу со стороны валков параллельно оси прокатки, уравновешивают силы натяжений полосы То и Т1.
, следовательно, силы Rx, действующие на полосу со стороны валков параллельно оси прокатки, уравновешивают силы натяжений полосы То и Т1.
Вертикальные проекции сил R представляют собой силы прокатки, приложенные к полосе в очаге деформации (они на рис. 10.2 изображены пунктиром):
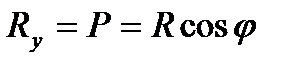 . (10.21)
. (10.21)
Следовательно, сила R равна:
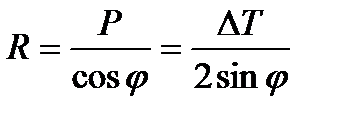 . (10.22)
. (10.22)
Из выражений (10.21), (10.22) можно определить угол j :
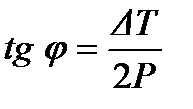 . (10.23)
. (10.23)
При отсутствии разности сил натяжений 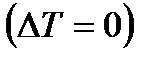 угол j=0, т.е. сила R становится вертикальной и равной силе прокатки Р.
угол j=0, т.е. сила R становится вертикальной и равной силе прокатки Р.
Проанализировав равновесие полосы, можно перейти к равновесию валка и определению момента М1, необходимого для его вращения в случае, когда на полосу действуют силы натяжений полосы, не равные между собой.
Согласно 3му закону Ньютона, со стороны полосы на валок действует сила R, равная по величине и противоположно направленная силе R, действующей со стороны валка на полосу. Силу R,действующую на валок (она обозначена на рис. 10.2 сплошной линией), можно разложить на две составляющие: силу прокатки Р и силу полуразности натяжений 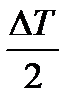 (также обозначенные сплошными линиями), которые равны и противоположно направлены соответствующим
(также обозначенные сплошными линиями), которые равны и противоположно направлены соответствующим
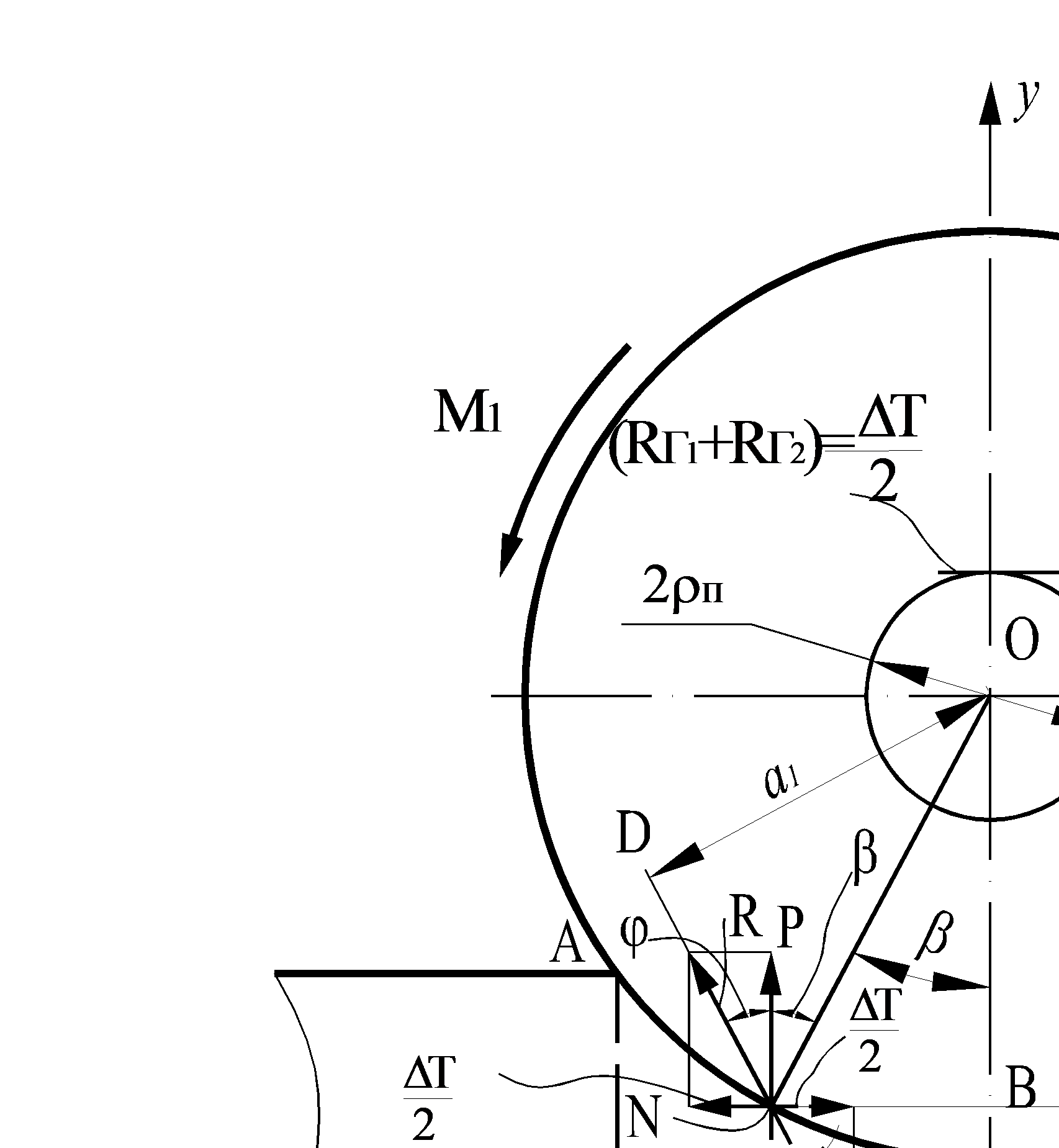
Рис. 10.2. Расчетная схема сил и моментов в двухвалковой клети при действии на полосу сил натяжений То,Т1 (вариант То > Т1) (обозначения величин объяснены в тексте). Пунктирными линиями обозначены силы, действующие со стороны валков на полосу, сплошными – силы, действующие со стороны полосы на валки.
силам Р и 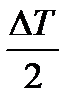 , действующим со стороны валка на полосу. Таким образом, уравнение равновесия моментов, действующих на валок, можно записать в виде:
, действующим со стороны валка на полосу. Таким образом, уравнение равновесия моментов, действующих на валок, можно записать в виде:
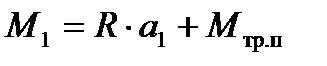 (10.24)
(10.24)
где а1 – плечо силы R относительно оси вращения валка.
Его величину можно определить из треугольника ОDN (см. рис. 10.2):
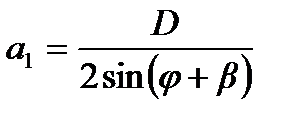 , (10.25)
, (10.25)
где угол b, показанный на рис 10.1 и 10.2, определяют через его синус по формуле (10.12). Как видно, при наличии натяжений, если 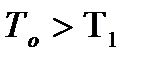 , момент силы R значительно больше, чем момент силы прокатки Ра, т.е. для компенсации разности натяжений
, момент силы R значительно больше, чем момент силы прокатки Ра, т.е. для компенсации разности натяжений 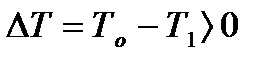 необходимо увеличивать момент главного привода валков.
необходимо увеличивать момент главного привода валков.
Следует отметить, что в ряде источников [1;15;23] при изложении методики расчета момента М1 для случая прокатки полосы с натяжениями допущена неточность: сила R, отклонившаяся от вертикали, отождествлена с силой прокатки Р и сумма моментов 2Ra1 приравнена к сумме моментов 2Ра1, которая названа моментом прокатки.
На самом деле сила R – это равнодействующая двух сил – прокатки и полуразности натяжений. Сила прокатки Р действует в вертикальной плоскости (даже при наличии натяжений, в чем легко убедиться, приравняв То = Т1) и силы реакций на неё (также вертикальные) возникают в нажимных устройствах рабочей клети.
Сила полуразности натяжений 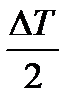 действует в горизонтальной плоскости и силы реакций на неё возникают также в горизонтальной плоскости между подушками валка и опорными плоскостями окон станин; они не влияют на нагрузку нажимных механизмов.
действует в горизонтальной плоскости и силы реакций на неё возникают также в горизонтальной плоскости между подушками валка и опорными плоскостями окон станин; они не влияют на нагрузку нажимных механизмов.
Поэтому расчет момента М1, целесообразно выполнять, вместо формулы (10.24), по формуле, в которой моменты сил прокатки и полуразности натяжений вычисляются отдельно (см. рис. 10.2):
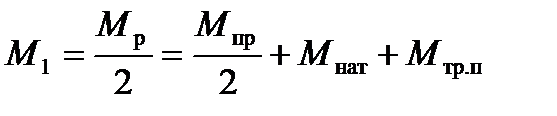 , (10.26)
, (10.26)
где Мпр =2Ра - момент прокатки (см. формулу (10.8));
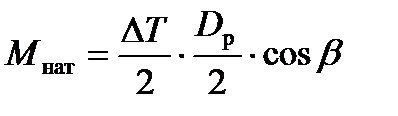 , (10.27)
, (10.27)
- момент полуразности сил заднего и переднего натяжений полосы;
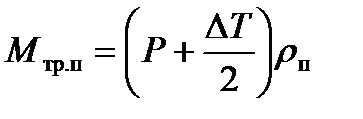 (10.28)
(10.28)
- момент сил трения в подшипниках, возникающих под воздействием сил прокатки и полуразности натяжений (сумма горизонтальных сил реакций в подушках 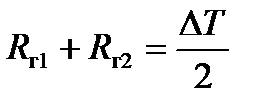 .
.
Подставив выражения (10.27) и (10.28) в формулу (10.26), после простых преобразований получим:
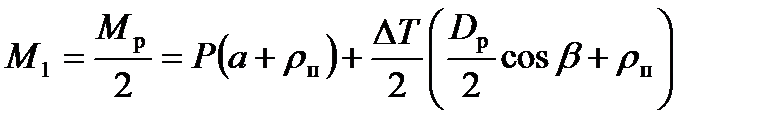 (10.29)
(10.29)
Смысл выражения (10.29) состоит в том, что момент М1, приводящий валок во вращение, преодолевает сопротивление двух моментов: пары сил {P, R1+R2 =P} c плечом (а + rп) и пары сил 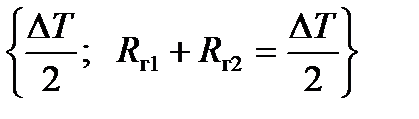 с плечом
с плечом 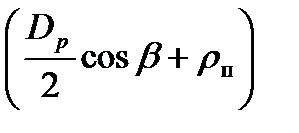 .
.
Все вышеперечисленные формулы относились к варианту технологического режима, при котором сила заднего натяжения То больше силы переднего натяжения Т1.
На практике бывают режимы, когда То < Т1 (например, в первой клети непрерывного стана холодной прокатки). Расчетная схема равновесия моментов, действующих на валок, для этого варианта распределения сил натяжений показана на рис. 10.3. В отличие от схемы рис. 10.2, сила полуразности натяжений 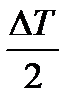 действует на валок в сторону движения полосы, создавая момент
действует на валок в сторону движения полосы, создавая момент
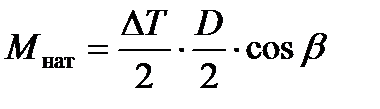 ,
,
направленный в ту же сторону, что и приводной момент М1. Следовательно, в том случае, когда Т1 > То, разность сил натяжений полосы разгружает главный привод стана, т.к. берет на себя часть нагрузки по осуществлению процесса прокатки.
Из рис. 10.3 видно, что вращающий момент одного валка в этом случае будет равен:
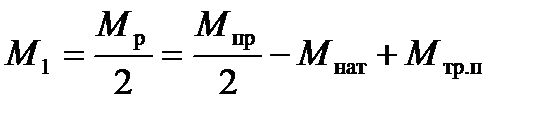 (10.30)
(10.30)
Выражение (10.30) отличается от выражения (10.26) только знаком момента Мнат, причем величины Мнат и Мтр.п вычисляются по тем же формулам (10.27), (10.28), что и для случая, когда Т1 < То.
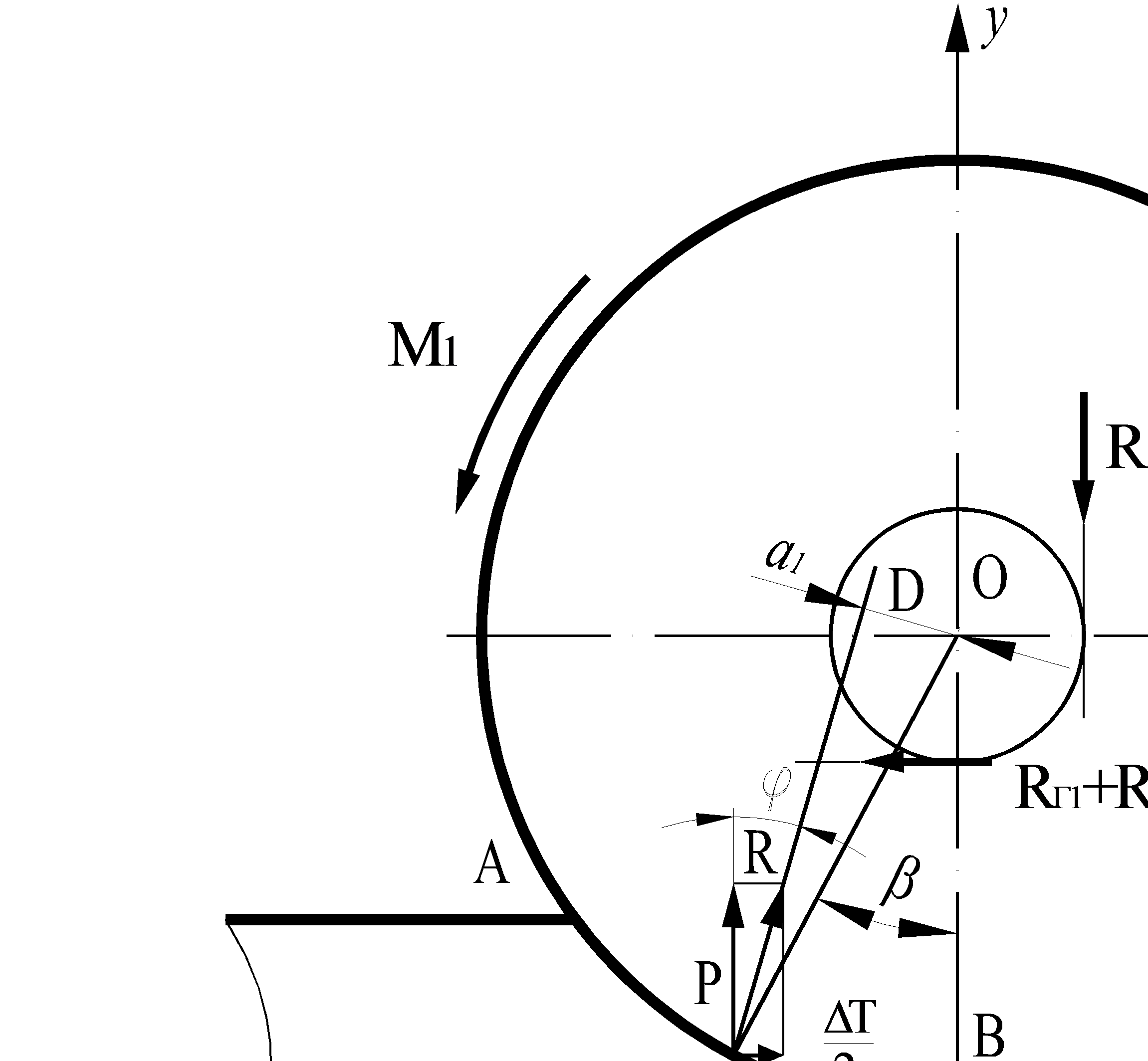
Рис. 10.3 Расчетная схема сил и моментов, действующих на верхний валок двухвалковой клети при соотношении натяжений полосы Т1 > Т.
Равнодействующая сила R сил Р и 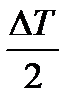 , приложенных к валку со стороны полосы, как видно из схемы рис. 10.3, отклонена от вертикали вперед по ходу прокатки, в результате её плечо а1 относительно оси валка, значительно меньше плеча а в схеме рис. 10.2 и меньше плеча а силы прокатки Р.
, приложенных к валку со стороны полосы, как видно из схемы рис. 10.3, отклонена от вертикали вперед по ходу прокатки, в результате её плечо а1 относительно оси валка, значительно меньше плеча а в схеме рис. 10.2 и меньше плеча а силы прокатки Р.
Из треугольника OND видно, что это плечо равно:
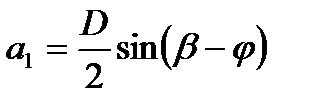 . (10.31)
. (10.31)
Согласно формуле (10.23), величина угла j между силами Р и R зависит от отношения величин сил и 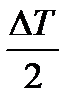 и Р. При увеличении силы переднего натяжения и при небольшом обжатии (когда сила Р невелика) возможен случай, когда угол j, увеличиваясь, станет равен углу b. Тогда, согласно (10.31), плечо а1 будет равно нулю, т.е. сила R пройдет через ось валка.
и Р. При увеличении силы переднего натяжения и при небольшом обжатии (когда сила Р невелика) возможен случай, когда угол j, увеличиваясь, станет равен углу b. Тогда, согласно (10.31), плечо а1 будет равно нулю, т.е. сила R пройдет через ось валка.
Расчетная схема для этого случая показана на рис. 10.4. Чтобы лучше понять равновесие моментов, действующих на валок, в этой схеме сила R не разложена на составляющие Р и 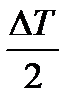 .
.
Тогда суммарные силы опорных реакций Rсум1, Rсум2 (от действия силы прокатки Р и полуразности сил натяжений 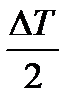 ), согласно условию равновесия сил, направлены параллельно силе R, по касательной к кругу трения в подшипниках, и уравнение равновесия моментов будет иметь вид:
), согласно условию равновесия сил, направлены параллельно силе R, по касательной к кругу трения в подшипниках, и уравнение равновесия моментов будет иметь вид:
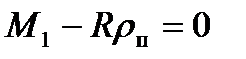 ,
,
где 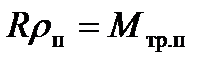 - суммарный момент сил трения в подшипниках.
- суммарный момент сил трения в подшипниках.
Откуда: 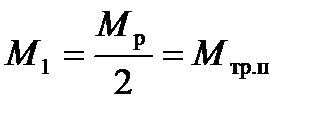 .
.
Следовательно, если сила R проходит через ось валка (когда j = b), со стороны главного привода требуется приложить только момент, равный моменту трения в подшипниках, а момент прокатки прикладывать не требуется, т.к. соответствующую нагрузку берет на себя разность сил натяжений полосы.
При дальнейшем увеличении разности сил натяжений Т1 - То = DТ угол j становится еще больше и может увеличиться до значения: j > b. Сила R для этого случая обозначена на схеме рис. 10.4. пунктирной линией. Её плечо – отрезок OD – равно:
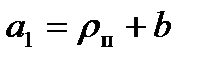
Следовательно, уравнение равновесия моментов для этого случая имеет вид:
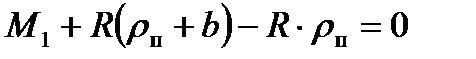 .
.
Откуда требуемый момент со стороны привода равен:
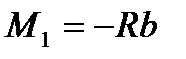 .
.
Знак минус означает, что со стороны главного привода вообще не требуется прикладывать момент, т.к. прокатка осуществляется силой разности натяжений полосы, при этом двигатель главного привода валков работает в генераторном режиме.
По описанному принципу сконструированы роликовые волочильные станы: их рабочие ролики являются холостыми, а процесс волочения осуществляется силой переднего натяжения обрабатываемого металла.
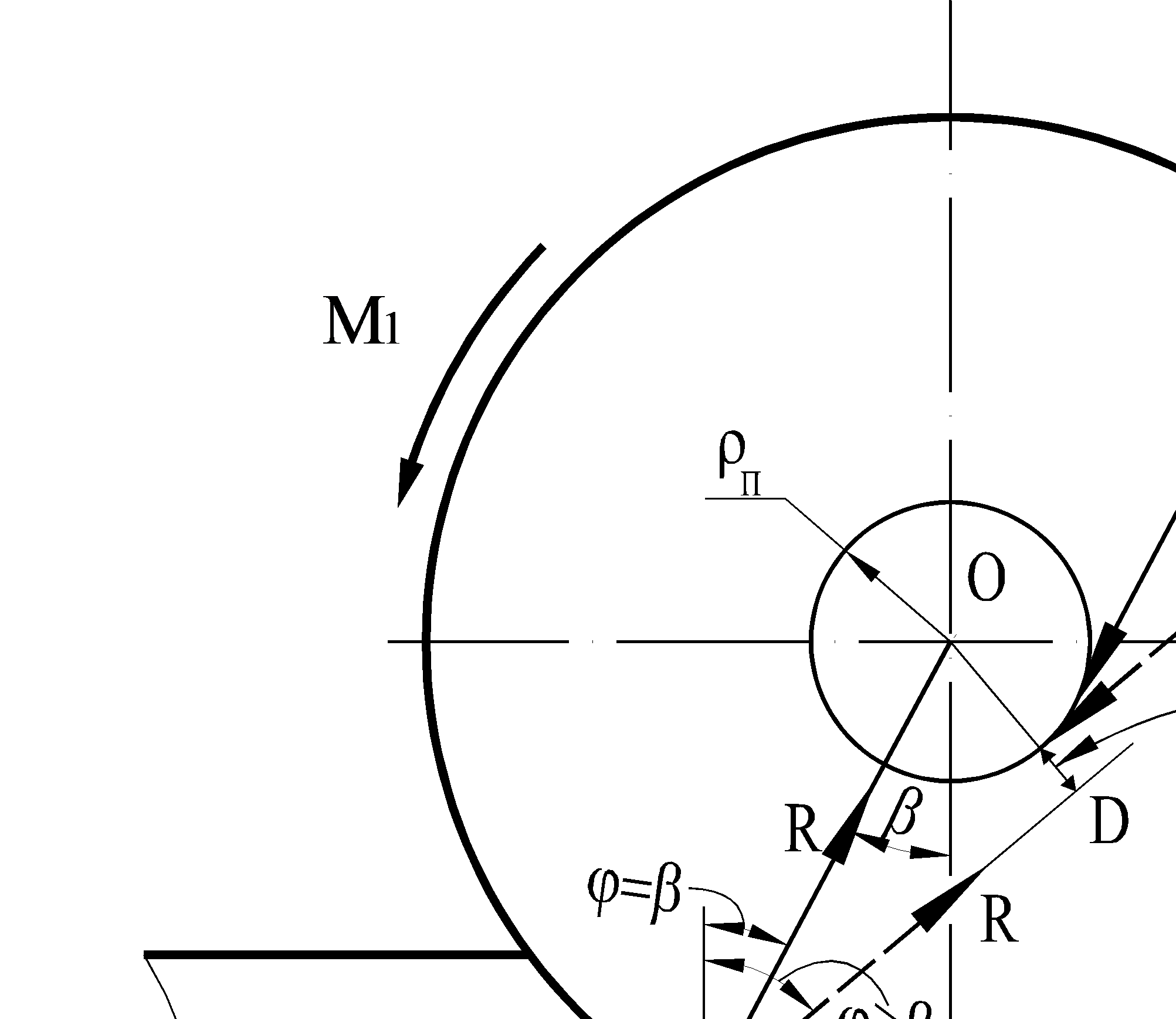
Рис. 10.4. Расчетные схемы сил и моментов, действующих на
верхний валок двух валковой клети при соотношении натяжений
полосы Т1 > То, если: а) j = b; б) j > b.
б) Прокатка ведется с переменной скоростью
Этот случай характерен для технологического процесса многих прокатных станов. На реверсивных станах при каждом реверсе скорость полосы уменьшается до нуля, а потом увеличивается в противоположном направлении до рабочего значения. В технологии непрерывных широкополосных станов горячей прокатки предусмотрен специальный режим – прокатка с ускорением – для поддержания постоянной температуры конца прокатки. На непрерывных станах холодной прокатки обработку участка полосы со сварным швом производят на пониженной скорости, для чего сначала её снижают, а затем увеличивают до рабочей скорости.
Наиболее важно при расчете необходимого момента главного привода учесть случай, когда прокатка ведется с ускорением, т.к. в этом случае двигатель должен приложить к валкам такой приводной момент, чтобы преодолеть не только моменты прокатки, сил трения в подшипниках и сил разности заднего и переднего натяжений, но и дополнительный динамический момент, возникающий из-за силы инерции ускоряемой полосы и из-за моментов инерции валков и узлов линии главного привода, вращающихся с угловым ускорением. Дополнительный динамический момент, который необходимо приложить к каждому валку со стороны главного привода, в этом случае будет равен:
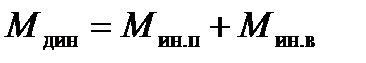 , (10.32)
, (10.32)
где Мин.п – момент сопротивления вращению валка, возникающий от силы инерции ускоряемой полосы; Мин.в – момент сопротивления вращению ускоряемого валка и других элементов линии главного привода, возникающий от моментов их инерции.
Ниже приведены методики расчета моментов, входящих в (10.32).
Расчет величины Мин.п
При прокатке полосы в i -й клети n - клетевого стана с ускорением величины ускорений будут разные для участков полосы, находящейся перед клетью и после выхода её из клети:
- перед клетью:
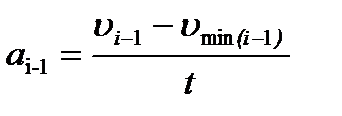 ; (10.33)
; (10.33)
- за клетью:
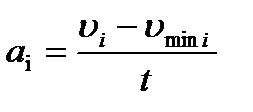 (13.34)
(13.34)
где t - текущее время прокатки с ускорением, с; 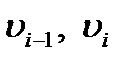 - переменные скорости полосы соответственно перед и за i-й клетью, м/с;
- переменные скорости полосы соответственно перед и за i-й клетью, м/с; 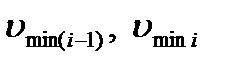 - минимальные скорости полосы соответственно перед и за i-й клетью (например, скорости прокатки концевых участков полос, содержащих сварной шов), м/с.
- минимальные скорости полосы соответственно перед и за i-й клетью (например, скорости прокатки концевых участков полос, содержащих сварной шов), м/с.
Указанные скорости связаны зависимостями, вытекающими из закона постоянства секундного объема полосы:
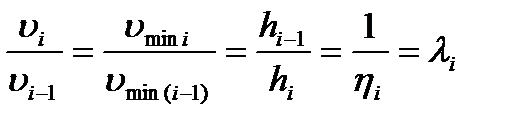 (10.35)
(10.35)
где 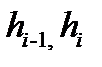 - толщина полосы на входе в i-ю клеть и на выходе из неё;
- толщина полосы на входе в i-ю клеть и на выходе из неё;
hi - коэффициент обжатия в i-й клети, li- коэффициент вытяжки в i-й клети.
Из соотношений (10.33), (10.34), (10.35) следует:
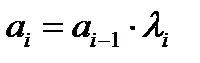 ,
,
т.е. коэффициентом пропорциональности для ускорений перед и за i-й клетью, как и для соответствующих скоростей полосы, является коэффициент вытяжки в этой клети.
В связи с изложенным, сила инерции, действующая на полосу при прокатке с ускорением, складывается из двух сил (см. схему на рис.10.5):
- перед клетью:
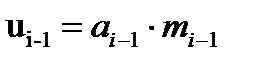 (10.36)
(10.36)
- за клетью:
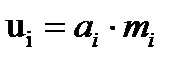 ,
,
где 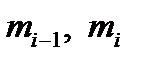 - массы участков полосы, находящихся перед и за i-й клетью, равные:
- массы участков полосы, находящихся перед и за i-й клетью, равные:
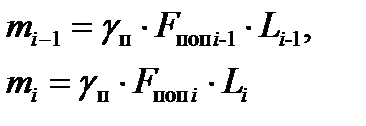 (10.37)
(10.37)
gп – площадь материала полосы;
Fпоп i-1 , Fпоп i - площади поперечного сечения полосы на входе в i-ю клеть и выходе из неё;
Li-1, Li - длины участков полосы, находящихся перед и за i-й клетью.
Если стан одноклетевой, без моталки, то силы 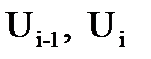 - суммируются и на валки со стороны полосы действует инерционная сила:
- суммируются и на валки со стороны полосы действует инерционная сила:
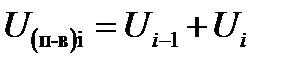 ,
,
а на каждый валок действует половина этой силы: 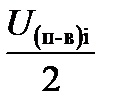 .
.
Если стан имеет больше, чем 1 рабочую клеть, и снабжен моталкой, то величина инерционной силы, действующей на валки i-й клети со стороны полосы, зависит от настройки системы управления натяжением полосы и скоростным режимом стана.
Поскольку активное воздействие на движение полосы валки могут оказывать только в зоне отставания (это объяснено в главе 9), целесообразно так настраивать стан, чтобы привод валков i-й клети преодолевал инерционное сопротивление участка полосы, находящегося перед клетью, а инерционное сопротивление участка полосы, находящегося на выходе из i-й клети, преодолевали валки следующей, (i +1)-й клети или моталка.
В этом случае на валки i-й клети будет действовать инерционная сила:
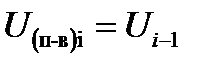 .
.
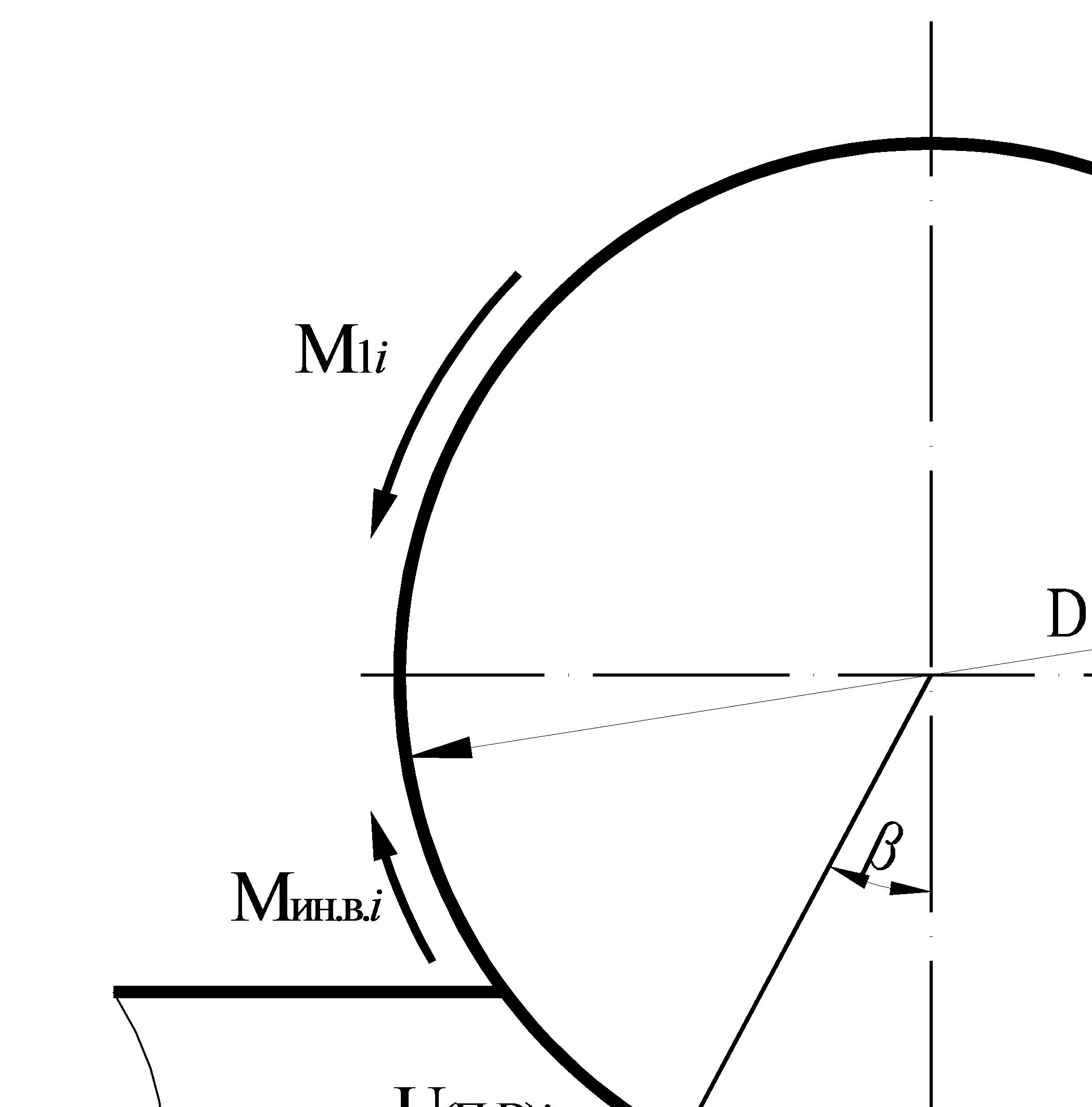
Рис. 10.5 Схема к расчету динамического момента, действующего
на валок при прокатке с ускорением
Момент сопротивления вращению каждого валка, вызванный силой инерции ускоряемой полосы, согласно схеме рис.10.5, равен:
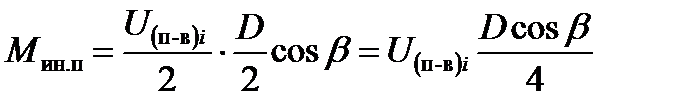 (10.38)
(10.38)
где D - диаметр бочки валка; b - угол, определяющий точку приложения силы 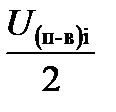 .
.
Выражение (10.38) основано на допущении, что сила, действующая на валок от силы инерции полосы, приложена в той же точке, где и сила прокатки. Это допущение вносит некоторую погрешность в расчет величины 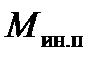 , однако она невелика, т.к. угол b достаточно мал и величина cos b близка к единице.
, однако она невелика, т.к. угол b достаточно мал и величина cos b близка к единице.
Поэтому на тонколистовых станах величину 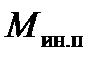 можно рассчитывать по формуле:
можно рассчитывать по формуле:
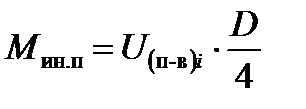 . (10.39)
. (10.39)
В качестве примера рассчитаем момент сопротивления вращению валка 4й клети 5ти клетевого стана 1700, (Dp=0,5 м) вызванный силой инерции стальной полосы, прокатываемой с ускорением а4 = 1м/с2. Размеры полосы: ширина b=1м, толщины: на входе в клеть h3 =1,1м, на выходе из клети h4= 0,85мм, плотность стали g = 7850 кг/м3; расстояние между клетями: Li-1 = Li =4,5м. Считаем, что валки 4й клети воздействуют только на участок полосы между 3й и 4й клетями, а участок между 4й и 5й клетями ускоряется валками 5й клети. Ход расчета:
а) массу ускоряемой части полосы определяем по формуле (10.37):
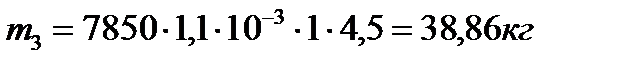
в) силу инерции ускоряемой части полосы определим по формуле (10.36):
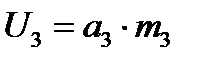 , где а3 – ускорение участка полосы на выходе из 3й клети, равное:
, где а3 – ускорение участка полосы на выходе из 3й клети, равное:
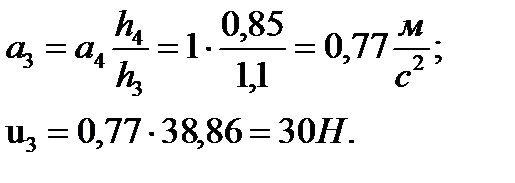
г) искомый момент сопротивления вращению каждого валка 4й клети, вызванный силой инерции полосы, определим по формуле (10.39):
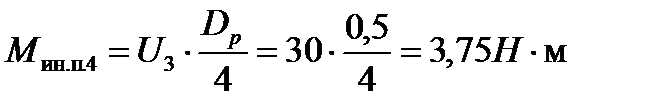
Расчет величины Мин.в.
Момент сопротивления вращению валка и связанных с ним деталей линии главного привода при прокатке с ускорением следует рассчитывать по классической формуле теоретической механики:
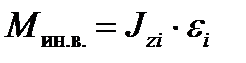 , (10.40)
, (10.40)
где Jzi – суммарный момент инерции валка i-й клети и других вращающихся деталей линии его главного привода, кг×м2, ei - угловое ускорение валка i-й клети, 1/с2.
Покажем, что размерность произведения в правой части формулы (10.40) соответствует обычной размерности момента Н×м.
Согласно системе СИ, размерность Ньютона: 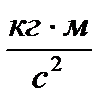 . Следовательно, произведение:
. Следовательно, произведение:
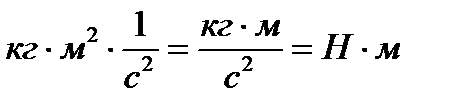 .
.
Рассмотрим методы определения величин Jzi и ei, входящих в формулу (10.40).
Для определения Jzi необходимо вычислить по отдельности моменты инерции прокатного валка, шпинделей, муфт и других узлов линии его привода, а затем все эти моменты инерции просуммировать. Чтобы использовать общую терминологию для двухвалковой и многовалковых клетей, будем называть прокатные валки двухвалковой клети рабочими валками, (в многовалковых клетях так называют валки, непосредственно контактирующие с прокатываемым металлом).
Все вращающиеся элементы линии главного привода, в том числе и сам рабочий валок можно схематически представить как совокупность цилиндров, которые могут быть сплошными или полыми.
Поэтому для расчета их моментов инерции следует воспользоваться классическими формулами теоретической механики:
а) момент инерции сплошного цилиндра относительно оси его вращения z:
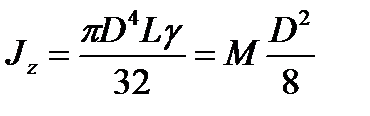 , (10.41)
, (10.41)
где D - наружный диаметр цилиндра, м; L - его длина, м; g - плотность материала цилиндра, 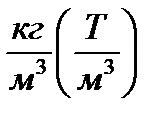 ; М – масса цилиндра, кг (т).
; М – масса цилиндра, кг (т).
б) Момент инерции полого цилиндра (имеющего осевое цилиндрическое отверстие) относительно оси его вращения z:
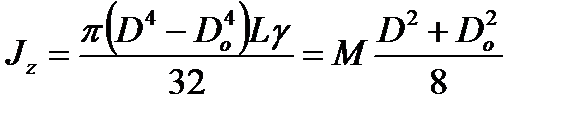 , (10.41а)
, (10.41а)
где Dо – диаметр осевого отверстия.
Примечание. В большинстве ранее изданных учебников и справочников по теории прокатки рекомендуется при расчете динамического момента использовать не моменты инерции Jz, а так называемые маховые моменты вращающихся элементов главной линии 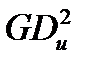 , где G - вес тела, а Dи – диаметр его инерции. Однако во всех упомянутых источниках не указано, как вычислять Dи, поэтому применение величины
, где G - вес тела, а Dи – диаметр его инерции. Однако во всех упомянутых источниках не указано, как вычислять Dи, поэтому применение величины 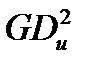 которое было распространено, когда в инженерных расчетах использовали техническую систему единиц, в настоящее время нецелесообразно: это усложняет расчеты из-за необходимости вычислять диаметры инерции и приводит к ошибкам, связанным с переводом единиц из технической системы в международную.
которое было распространено, когда в инженерных расчетах использовали техническую систему единиц, в настоящее время нецелесообразно: это усложняет расчеты из-за необходимости вычислять диаметры инерции и приводит к ошибкам, связанным с переводом единиц из технической системы в международную.
В качестве примера определим момент инерции стального рабочего валка 4й клети 5ти клетевого стана 1700 с осевым цилиндрическим отверстием, размеры которого указаны в таблице:
| Параметр | Диаметр бочки | Диаметр осевого отверстия | Длина бочки | Диаметр шейки | Длина шейки | Диаметр приводного конца | Длина приводного конца |
| Обозначение | Dp | Do | Lp | dш | lш | Dпк | Lпк |
| Численное значение, мм |
Как видно из таблицы, рабочий валок схематично можно представить как совокупность пяти полых стальных цилиндров: бочки, двух шеек и двух приводных концов. Следовательно, для расчета момента инерции валка надо по формуле (10.41а) вычислить моменты инерции его составных элементов, а затем их просуммировать (плотность стали g = 7850 кг/м3).
Момент инерции бочки (для удобства расчёта размеры переводим в метры):
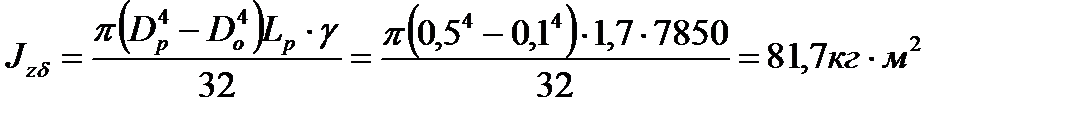 .
.
Момент инерции шейки:
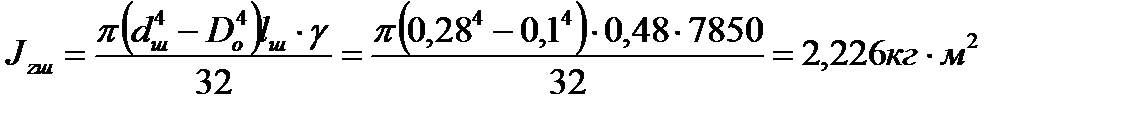 .
.
Момент инерции привода конца:
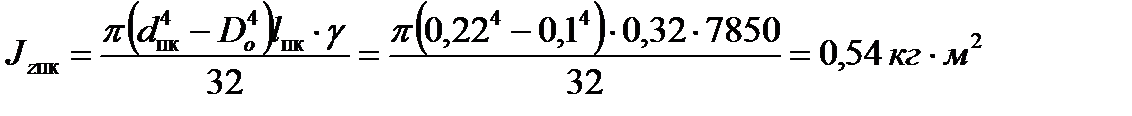 .
.
Момент инерции рабочего валка:
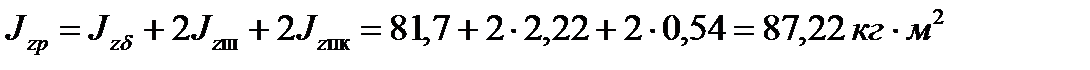 .
.
Угловое ускорение рабочего валка i-й клети ei, входящее в формулу (10.40), определяют с использованием классических формул теоретической механики:
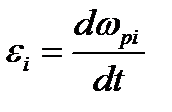 , (10.42)
, (10.42)
где 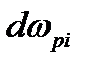 - угловая скорость вращения рабочего валка, 1/с, равная:
- угловая скорость вращения рабочего валка, 1/с, равная:
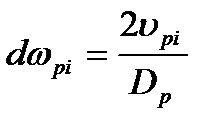 ; (10.43)
; (10.43)
где 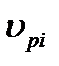 - окружная скорость поверхности бочки рабочего валка, м/с.
- окружная скорость поверхности бочки рабочего валка, м/с.
В главе 5 показано, что из-за опережения в очаге деформации скорость полосы на выходе из валков i-й клети 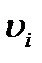 не совпадает с окружной скоростью бочки
не совпадает с окружной скоростью бочки 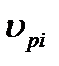 :
:
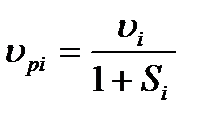 , (10.44)
, (10.44)
где Si - коэффициент опережения в i-й клети (методы его расчета изложены в главе 5).
Из (10.42), (10.43), (10.44) получим:
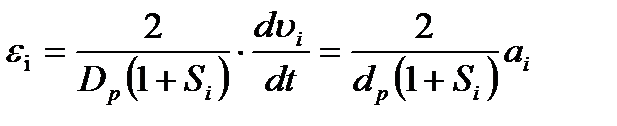 (10.45)
(10.45)
Формула (10.45) позволяет определить угловое ускорение рабочего валка i-й клети, необходимое, чтобы обеспечить ускорение полосы на выходе из этой клети, равное ai. Например, если задано ускорение полосы в 4й клети (i=4) 5ти клетевого стана 1700 a4 = 1м/с2, то при значениях Dр =0,5м и S4 =0,05 получим требуемое угловое ускорение рабочих валков:
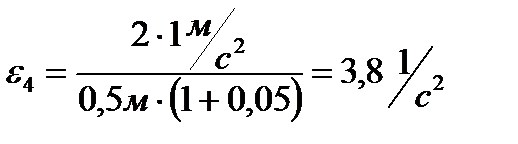 .
.
Тогда момент инерционного сопротивления вращению для валка, с размерами, указанными в приведенной выше таблице, согласно формуле (10.40), равен:
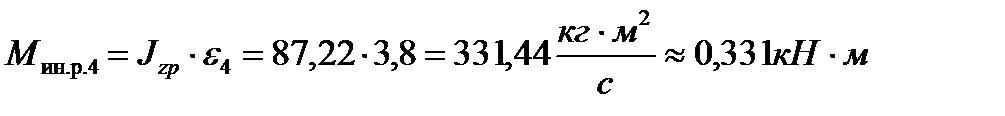 .
.
Следовательно, дополнительный динамический момент, который необходимо приложить к каждому рабочему валку 4й клети со стороны главного привода, чтобы преодолеть инерционное сопротивление полосы и самого рабочего валка, согласно формуле (10.32) будет равен:
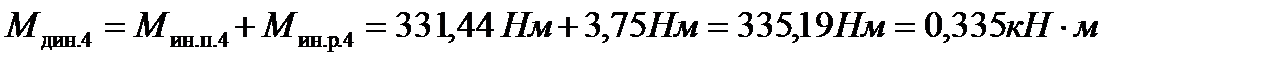 .
.
Из приведенного примера видно, что доля динамического момента, приходящаяся на преодоление силы инерции полосы, составила 1,3%, т.е. при прокатке тонких полос ею можно пренебречь.
Иное положение в рабочих клетях, где прокатывают толстые полосы.
Например, при тех же исходных данных, при которых выполнен пример расчета  , если толщина полосы на входе в клеть равна 50мм, на выходе из клети 35мм, а ширина 1,3м, что соответствует условиям горячей прокатки полос в черновой клети широкополосного стана, масса ускоряемой полосы по формуле (10.37) будет равна:
, если толщина полосы на входе в клеть равна 50мм, на выходе из клети 35мм, а ширина 1,3м, что соответствует условиям горячей прокатки полос в черновой клети широкополосного стана, масса ускоряемой полосы по формуле (10.37) будет равна:
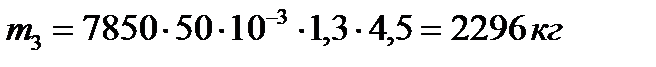 .
.
Сила инерции по формуле (10.36):
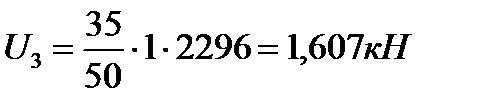 .
.
Момент сопротивления вращению валка, вызванный силой инерции полосы, по формуле (10.39) (диаметр валка Dр =0,8м):
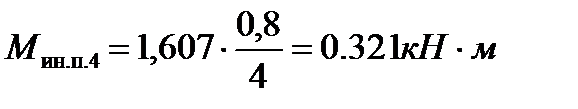 .
.
Эта величина почти в 100 раз больше, чем при прокатке тонкой полосы, она сопоставима с величиной момента сопротивления вращению, вызванного силой инерции рабочего валка.
в) Прокатка с несимметричным скоростным режимом верхнего и нижнего валков
Под несимметричным скоростным режимом верхнего и нижнего валков подразумевают такой режим, когда окружные скорости поверхности бочек валков неодинаковые. Это приводит к тому, что поверхностный слой полосы, контактирующий с поверхностью валка, имеющей бόльшую скорость, движется через очаг деформации быстрее, чем поверхностный слой полосы, контактирующий с другим валком.
В учебниках и монографиях по теории прокатки [4;15;27 и др.] рассматриваются методы определения направлений действия сил и расчета моментов, действующих на валки, для нескольких вариантов несимметричных скоростных режимов прокатки:
- прокатка в валках, имеющих небольшую разницу диаметров бочек и одинаковые угловые скорости;
- прокатка в валках, имеющих большую разницу диаметров и разные угловые скорости;
- прокатка с одним приводным валком, а другим – холостым (например, при поломке одного из шпинделей);
- прокатка с разными коэффициентами трения на поверхностях контакта полосы с верхним и нижним валками;
- горячая прокатка металла, неравномерно нагретого по толщине и имеющего из-за этого разные сопротивления пластической деформации в контакте с верхним и нижним валками.
Методы определения направлений сил и расчета моментов, излагаемые в указанных источниках, носят качественный характер или основаны на эмпирических данных, оценка погрешности этих методов не приводится.
Это связано со следующей особенностью несимметричного режима прокатки, характерной для всех перечисленных выше его вариантов.
Валок с меньшей окружной скоростью бочки, даже имеющий работоспособный привод, по сути, работает как холостой, т.к. полоса, движущаяся быстрее за счет воздействия другого валка, вращает отстающий валок касательными силами, создающими для него приводной момент. В результате двигатель отстающего валка работает в генераторном режиме, а суммарный приводной момент обеспечивается приводом валка с бόльшей окружной скоростью. Из этого следует, что очаг деформации полосы со стороны отстающего валка целиком состоит из зоны опережения, а со стороны более быстрого валка очаг деформации обычный: вначале он имеет зону отставания, а затем переходит в зону опережения.
Однако в классической теории прокатки не рассматривалось решение задачи расчета контактных напряжений и сил в очаге, состоящем целиком из зоны опережения, а тем более – в несимметричном очаге, имеющем разные скоростные режимы в контакте с каждым валком. Поэтому точное положение равнодействующих контактных напряжений, а значит, и плечи сил прокатки, неодинаковые для верхнего и нижнего валков, в таком очаге деформации неизвестны. Следует признать, что энергосиловой расчет рабочей клети с несимметричным очагом деформации пока остается «белым пятном» в теории прокатки.
Учитывая изложенное, в данном учебнике методы энергосилового расчета рабочих клетей с различными вариантами несимметричного очага деформации не рассматриваются. Студенты, аспиранты и специалисты, столкнувшиеся в своей практике с подобными очагами деформации, имеют возможность познакомиться с приближенными методами их расчета с помощью упомянутых выше литературных источников.
Для достоверного определения контактных напряжений и деформаций металла в несимметричном очаге деформации можно также использовать компьютерную программу «Deform -3D», или «Deform-2D», основанную на методе конечных элементов [26].
Дата добавления: 2019-02-08; просмотров: 1158;











